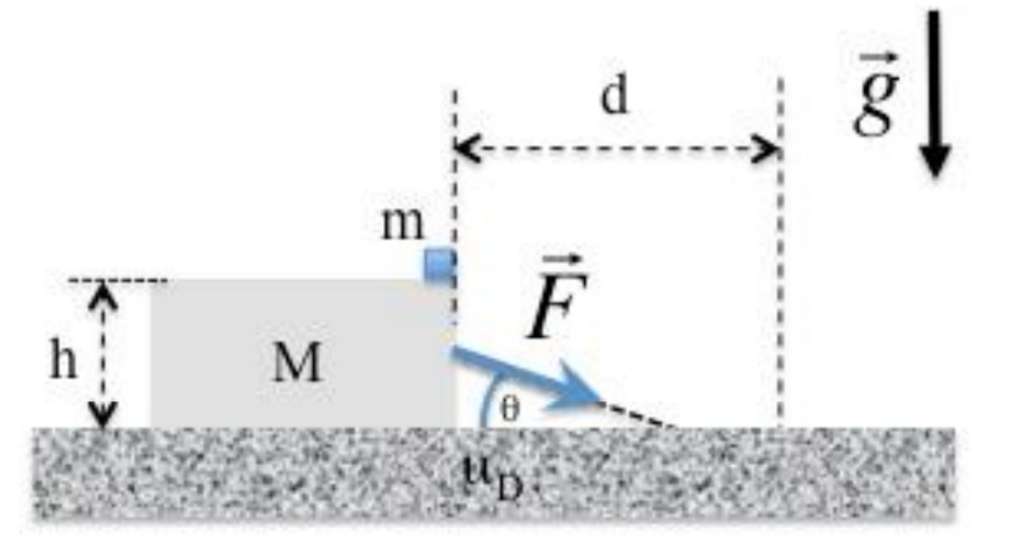
Si consideri un blocco di massa M=1.35 kg posto su un piano orizzontale scabro con
coefficiente di attrito dinamico µD=0.250 a cui è applicata una forza costante F che forma
con l'orizzontale un angolo $\theta $ =40 gradi
, cosicché la forza F (di modulo 10.7 N) ha una
componente diretta verso il basso. Al di sopra del blocco M viene posto un oggetto di
massa m=419 g di dimensioni trascurabili, che può essere considerato puntiforme. Tra il
punto materiale m ed il blocco M vi è attrito. In tali condizioni l'attrito fa sì che non vi sia
moto relativo tra i due corpi. Se i due corpi sono inizialmente fermi, calcolare:
l'accelerazione con cui i due corpi si muovono
Allora io per risolverlo ho provato in più modi diversi e quello che si avvicina di più al risultato di 1.21 ms^-2 è :
$$ \sum F_{y} = 0 quindi: - Fsin(\theta) - (M+m) g - (m+M) asin(\theta) + R = 0$$ (dove R è la reazione vincolare), mentre $$ \sum F_{x} = (M+m) acos(\theta) quindi : Fcos(\theta) - \mu _{d} R = (M+m) a cos (\theta)$$
Dove ho sbagliato? In caso avessi sbagliato, come andrebbe fatto? Grazie in anticipo

