Credo di aver risolto il seguente esercizio senza utilizzare un'ipotesi data:
If a mapping \(\displaystyle f:[0,1]→[0,1] \) is continuous, \(\displaystyle f(0)=0, f(1)=1 \) and \(\displaystyle (f\circ f)(x)\equiv x \) on \(\displaystyle [0,1]\Rightarrow f(x)\equiv x \).
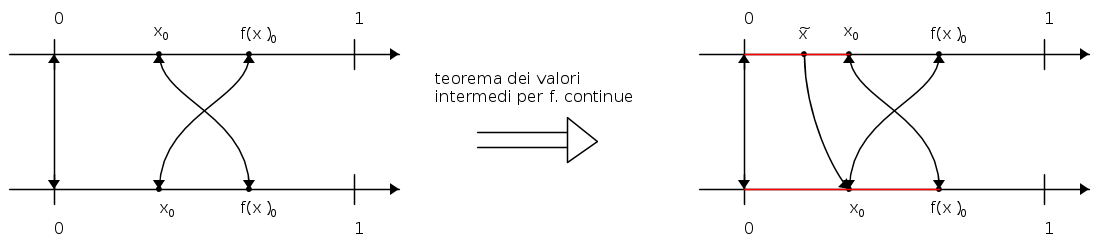
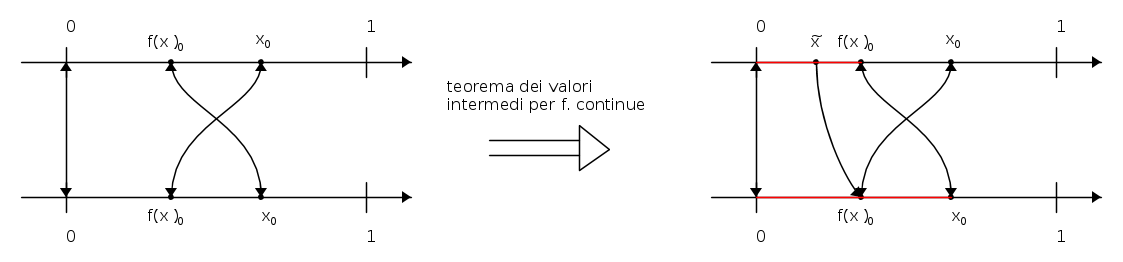
Senza stare a riportare la dimostrazione formale, la riporto direttamente in forma visiva che è immediata.
\(\displaystyle f(f(x))≡x \Rightarrow f \) invertibile, in particolare è iniettiva. Se per assurdo esistesse un \(\displaystyle x_0\in [0,1] \) tale che \(\displaystyle f(x_0 )>x_0 \):
che è assurdo perché \(\displaystyle f \) deve essere iniettiva.
Analogamente se fosse \(\displaystyle f(x_0)<x_0 \):
In entrambi i casi, da nessuna parte uso l'ipotesi che \(\displaystyle f(1)=1 \).
Sbaglio qualcosa?
3 messaggi
• Pagina 1 di 1
Re: Esercizio sulle funzioni continue
In realtà esistono più funzioni con la proprietà $f(f(x))=x$: una è chiaramente $f(x)=x$, ma un'altra è $f(x)=1-x$ (difatti $f(f(x))=1-(1-x)=x$).
Quindi le condizioni $f(0)=0$ ed $f(1)=1$ ti devono servire a scegliere $f(x)=x$ a scapito di altre alternative.
Quindi le condizioni $f(0)=0$ ed $f(1)=1$ ti devono servire a scegliere $f(x)=x$ a scapito di altre alternative.
Sono sempre stato, e mi ritengo ancora un dilettante. Cioè una persona che si diletta, che cerca sempre di provare piacere e di regalare il piacere agli altri, che scopre ogni volta quello che fa come se fosse la prima volta. (Freak Antoni)
-

gugo82 - Cannot live without

- Messaggio: 23948 di 44972
- Iscritto il: 12/10/2007, 23:58
- Località: Napoli
Re: Esercizio sulle funzioni continue
Nel tuo esempio, fissare solo \(\displaystyle f(0)=0 \) già mi esclude \(\displaystyle f(x)=1-x \).
Non ho capito se mi stai dicendo che la dimostrazione in [1] è sbagliata o meno.
Non ho capito se mi stai dicendo che la dimostrazione in [1] è sbagliata o meno.
- Silent
- Senior Member

- Messaggio: 637 di 1609
- Iscritto il: 23/02/2013, 15:40
3 messaggi
• Pagina 1 di 1
Torna a Analisi matematica di base
Chi c’è in linea
Visitano il forum: pilloeffe e 1 ospite