Naturalmente comprensiva della mia idea di come dovrebbero andare le cose:
Testo nascosto, fai click qui per vederlo
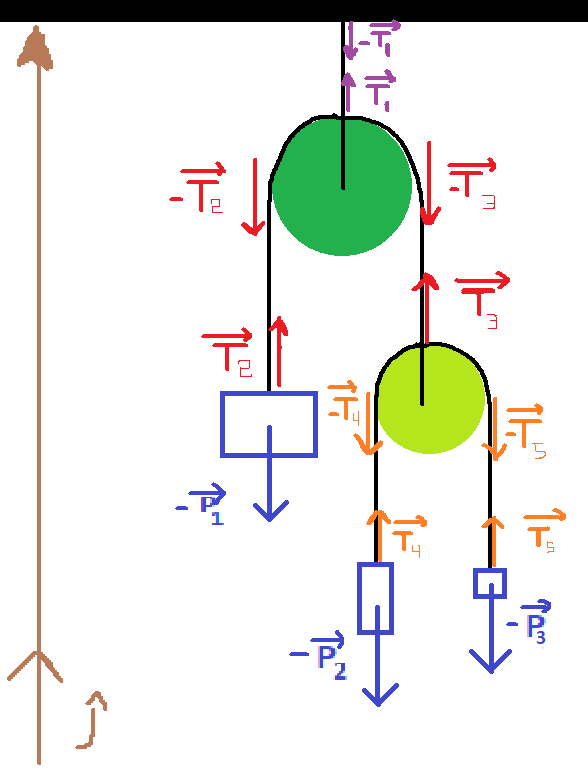
In particolare riporto la consegna dell'esercizio:
"Dati $m_1=2.5Kg, m_2=1.8 Kg$ e $m_3=2.2 Kg$, calcolare le accelerazioni delle
masse e le tensioni delle funi. (Funi e carrucole sono ideali)."
Queste sono le mie considerazioni: Il filo che passa sulla carrucola verde chiaro è unico, ideale e continuo per cui la tensione è una costante ed è pertanto uguale ovunque. Motivo per cui $T_4 = T_5$ e chiamerò questa d'ora in avanti $T'$. Analoga considerazione ho mosso nei confronti della carrucola verde scuro per cui nel risolvere ho considerato $T_2=T_3$ indicata come $T$. Applicando il secondo principio della dinamica alle due carrucole ottengo nell'ordine che $T = 2T'$
A questo punto applico il secondo principio della dinamica ai pesetti $2$ e $3$ ottenendo rispettivamente che
$T'-m_2g = m_2a_2$
$T'-m_3g = m_3a_3$
Applicando il secondo principio al pesetto $1$ ottengo invece che
$2T' -m_1g = m_1a_1$
A questo punto ho pensato che il filo ideale sulla carrucola in basso ponesse un vincolo cinematico sul modulo dell'accelerazione dei pesetti $2$ e $3$ che dovranno quindi essere uguali. In particolare l'accelerazione di uno sarà in verso opposta alla rimanente. Ad esempio scelgo di porre che il pesetto $2$ salga verso l'alto mentre $3$ scenda. Chiamando $a_23$ l'accelerazione comune si scrive che:
\(\begin{cases} T'-m_2g = m_2a_{23} \\ T'-m_3g = -m_3a_{23} \end{cases} \implies \begin{cases} T' =m_2(g +a_{23}) \\ (m_2-m_3)g = -(m_2+m_3)a_{23} \end{cases} \implies a_{23} = \frac{m_3-m_2}{m3+m2}g\)
da cui ricaverei anche che $T' = m_2(1+\frac{m_3-m_2}{m_3+m_2})g$
A questo punto $a_1 = 2\frac{m_2}{m_1}(\frac{m_3-m_2}{m_3+m_2})$ mentre $T = 2m_2(1+\frac{m_3-m_2}{m_3+m_2})g$
Inultile dire che con i calcoli che ho attuato i risultati sono sbagliati. Cosa mi sono perso? Addirittura pare che $a_3 \ne a_2$ bah...

