[
continua dal precedente mio intervento]
Erasmus_First ha scritto:$a_b=(a_xb_x+a_yb_y+a_zb_z)/sqrt(b_x^2+b_y^2+b_z^2)$. [*]
3 Modulo del prodotto vettoriale Conoscendo $a_b$ (cioè la componente di
a nella direzione di
b, come riportato nella citazione), è facile (con Pitagora) ricavare l'altezza –diciamola $h$ – del triangolo
PAB rispetto al lato di lunghezza
b =
PB e quindi l'area del parallelogramma di lati consecutivi
a =
PA e
b =
PB (che è appunto il modulo del nostro prodotto vettoriale). Si trova
$(b·h)^2 = b^2·(a^2 – a_b^2) = (a_x^2+a_y^2+a_z^2)(b_x^2+b_y^2+b_z^2) -(a_xb_x+a_yb_y+a_zb_z)^2 =$
$=a_x^2b_y^2 +a_x^2b_z^2 + a_y^2b_x^2+a_y^2b_z^2 +a_z^2b_x^2 + a_z^2b_y^2 -2a_xb_xa_yb_y-2a_xb_xa_zb_z -2 a_yb_ya_zb_z) =$
$=(a_xb_y-a_yb_x)^2 +(a_yb_z-a_zb_y)^2+ (a_zb_x-a_xb_z)^2$;
|
a ×
b | = $sqrt((a_xb_y-a_yb_x)^2 +(a_yb_z-a_zb_y)^2+ (a_zb_x-a_xb_z)^2)$.
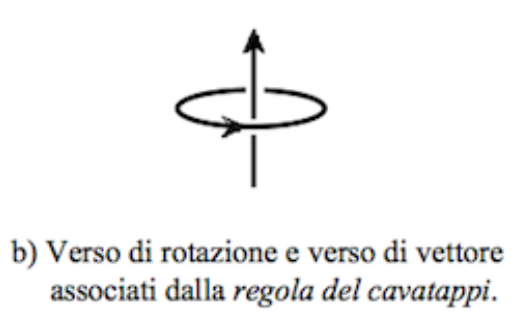
Hanno questo modulo tutti i vettori che hanno per componenti una delle 6 permutazione di ciascuna delle 8 terne $[±(a_xb_y-a_yb_x), ±(a_yb_z-a_zb_y), ±(a_zb_x-a_xb_z)]$; ma una sola di queste 6·8 =48 terne è ortogonale ad entrambi i fattori ed ha il verso dato dalla
"regola del cavatappi".
Abbiamo già visto che se il prodotto vettoriale fosse distributivo sarebbe;
$[a_x, a_y, a_z] × (b_x, b_y, b_z) = [a_yb_z-a_zb_y, a_zb_x-a_xb_z, a_xb_y_a_yb_x)]$.
Il modulo di questo vettore è quello giusto.
Consideriamo allora questo vettore e mostriamo che è lui il prodotto vettoriale
a ×
b in quanto, oltre al modulo, ha anche la direzione ed il verso voluti dalla definizione geometrica.
4 Controllo della direzione e del versoa) Occorre che
a ×
b sia ortogonale sia ad
a che a
b, cioè che risulti:
a · (
a ×
b) =
b · (
a ×
b)= 0. In effetti si ha:
$[a_x, a_y, a_z] · [a_yb_z-a_zb_y, a_zb_x-a_xb_z, a_xb_y_a_yb_x]=$
$=a_xa_yb_z-a_xa_zb_y + a_ya_zb_x-a_ya_xb_z +a_za_xb_y-a_za_yb_x = 0$;
$[b_x, b_y, b_z] · [a_yb_z-a_zb_y, a_zb_x-a_xb_z, a_xb_y_a_yb_x]=$
$=b_xa_yb_z-b_xa_zb_y + b_ya_zb_x-b_ya_xb_z +b_za_xb_y-b_za_yb_x = 0$.
b) Se scegliamo un riferimento cartesiano tale che
• l'origine
P dei segmenti orientati rappresentativi di
a e
b sia in [0, 0, 0],
• il termine
A del segmento orientato rappresentativo del 1° fattore
a stia sul semiasse positivo delle x e
• il termine
B del segmento orientato rappresentativo del 2° fattore
b stia nel piano (x, y) (nel quale è z=0)
il prodotto diventa del tipo:
$[a, 0, 0] × [b_x, b_y, 0] = [0, 0. a·b_y]$
nel quale è $a > 0$.
Giustamente la direzione del prodotto è quella dell'asse z e l'orientamento è quello per z crescenti se è $b_y > 0$ (e quello per z decrescenti se è $b_y < 0$).
Dunque è proprio
$[ a_x, a_y, a_z] × [b_x, b_y, b_z] = [a_yb_z-a_zb_x, a_zb_x-a_xb_z, a_xb_y-a_yb_x]$
perché solo così è rispettata la definizione di prodotto vettoriale.
5 Verifica della proprietà distributiva rispetto alla sommaA questo punto, la verifica della proprietà distributiva rispetto alla somma è immediata:
(
a ×
b) + (
a ×
c) = $[a_yb_z-a_zb_x, a_zb_x-a_xb_z, a_xb_y-a_yb_x] + [a_yc_z-a_zc_x, a_zc_x-a_xc_z, a_xc_y-a_yc_x]=$
$= [a_y(b_z + c_z) – a_z(b_x+c_x), a_z(b_x + c_x) – a_x(b_z+c_z), a_x(b_y+c_y)–a_y(b_x+c_x)]=$
a × (
b +
c) .
________