Buongiorno ho un problema nel risolvere il seguente esercizio
Il vettore X= ( X1,X2)ha distribuzione uniforme in {(X1,X2): 1< X1 < 2 0< X2 < X1-1}
Rappresentare graficamente X (sono riuscita a farlo)
Indicare il valore assunto della funzione di densità di X in (0.5 ; 0.25) e in (0.5 ; 0,75)
(QUI NON RIESCO AD ANDARE AVANTI COME FACCIO A FARLO SE NON HO fx1x2(x1,x2)?
Grazie
Stabilire se X1 E X2 sono indipendenti
determinare la funzione di densità e supporto di X2 tenendo conto che X1 ha assunto valore di 0,5
5 messaggi
• Pagina 1 di 1
Re: esercizio di probabilità
robertinad ha scritto:Rappresentare graficamente X (sono riuscita a farlo)
1) Dubito che questa sia la richiesta originale e corretta del problema; molto probabilmente la richiesta è "rappresentare graficamente il dominio (o supporto) di $X$, anche perché rappresentare la $X$ non vuol dire nulla....puoi rappresentare graficamente (ad esempio, ma nemmeno sempre) il supporto di una variabile, la sua pdf (che in questo caso però è una figura solida) ecc ecc
robertinad ha scritto:(QUI NON RIESCO AD ANDARE AVANTI COME FACCIO A FARLO SE NON HO fx1x2(x1,x2)?
2) stai calmina: ti rispondo solo perché sei appena iscritta ma qui chi urla non è ben accetto e quindi non riceve risposte.
3) le formule vanno scritte con l'apposito editor. Ti ho messo anche il link con le istruzioni
4) la traccia specifica che la pdf congiunta è uniforme sul dominio $mathcal{D}$ descritto nel testo del problema e quindi:
$f_(X_1X_2)(x_1,x_2)={{: ( 2 , ;(x_1,x_2)in mathcal{D}),( 0 , ;" altrove" ) :}$
....ora quello che hai chiesto di avere ce l'hai....
ciao
- tommik
- Moderatore

- Messaggio: 4693 di 11278
- Iscritto il: 23/04/2015, 13:13
- Località: Cassano Magnago
Re: esercizio di probabilità
Grazie per la risposta scusa non volevo "urlare" volevo far capire dove mi fermavo.
Confermo dice di rappresentare graficamente il supporto di X.
Non ho capire perché è 2.
Se $ [{ x1,x2) :1< x1 < 2, 0<x2<x1-1 } / $ $ mathcal{D} $$ mathcal{D} $
mentre per valutare il volere della funzione di densità di X in $ (0.5 ; 0.25) $ e in $ (0.5 ; 0.75) $
Come posso farlo?
Grazie
Confermo dice di rappresentare graficamente il supporto di X.
Non ho capire perché è 2.
Se $ [{ x1,x2) :1< x1 < 2, 0<x2<x1-1 } / $ $ mathcal{D} $$ mathcal{D} $
mentre per valutare il volere della funzione di densità di X in $ (0.5 ; 0.25) $ e in $ (0.5 ; 0.75) $
Come posso farlo?
Grazie
- robertinad
- Starting Member

- Messaggio: 2 di 6
- Iscritto il: 15/03/2019, 11:15
Re: esercizio di probabilità
Perfetto, penso di aver risolto
grazie
una conferma in generale :
se $ (P<a) $ $ c<x<d $. considerando $a>c$
allora faro
$ int_c^a int_(RRinX2) fxy(x,y) $
pero se ho come in questo caso
P(X=a)
$ int_a^a int_(RRinX2) fxy(x,y) $
Vero?
ovviamente inserisco anche la stessa condizione in x2 se necessario come in questo esercizio
grazie
una conferma in generale :
se $ (P<a) $ $ c<x<d $. considerando $a>c$
allora faro
$ int_c^a int_(RRinX2) fxy(x,y) $
pero se ho come in questo caso
P(X=a)
$ int_a^a int_(RRinX2) fxy(x,y) $
Vero?
ovviamente inserisco anche la stessa condizione in x2 se necessario come in questo esercizio
- robertinad
- Starting Member

- Messaggio: 3 di 6
- Iscritto il: 15/03/2019, 11:15
Re: esercizio di probabilità
robertinad ha scritto:Indicare il valore assunto della funzione di densità di X in (0.5 ; 0.25) e in (0.5 ; 0,75)
il valore assunto dalla densità di $X=(X_1,X_2)$ è 2 se sei nell'area del supporto1, zero altrimenti. Quindi dato che nei punti di coordinate $(X_1=0.5;X_2=0.25)$ e $(X_1=0.5;X_2=0.75)$ sei fuori dal triangolo in oggetto:
(cliccami per ingrandirmi)
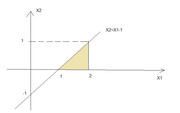
....il valore della densità nei punti dati è zero.
robertinad ha scritto:
Stabilire se X1 E X2 sono indipendenti
no, non lo sono e lo si vede dal supporto che non è rettangolare (condizione necessaria per l'indipendenza)
robertinad ha scritto:
determinare la funzione di densità e supporto di X2 tenendo conto che X1 ha assunto valore di 0,5
Questa richiesta invece è assolutamente senza senso, essendo ovviamente $f_(X_1)(0.5)=0$. Infatti, basta prendere la seguente definizione presa da un ottimo libro di probabilità (Cifarelli, Elementi di Calcolo delle Probabilità)
Def: sia $(X,Y)$ un vettore aleatorio continuo con funzione di densità $f_(XY)(x,y)$ e funzioni di densità marginali $f_X(x), f_(Y)(y)$.
La funzione di densità condizionale di $X$ dato $Y=y$ è la funzione definita da$f_(X|Y)(x|y)=(f_(XY)(x,y))/(f_Y(y))" ; "f_(Y)(y)>0$
...per concludere senza ombra di smentita che la densità condizionata richiesta non è definita.
Visto che la richiesta in questione è assolutamente insensata (non so se per un refuso di copiatura delll'OP o di stampa del prof) proviamo a rendere l'esercizio interessante. Innanzitutto poniamo il vettore $(X,Y)$ in modo da semplificare la notazione (evitando i pedici) e riformuliamo la seguente
robertinad ha scritto:determinare la probabilità che $Y<=1/4$ tenendo conto che $X$ ha assunto valore di $3/2$
partiamo dalla definizione della densità uniforme della traccia:
$f_(XY)(x,y)={{: ( 2 , ;(x,y)in mathcal(D)),( 0 , ;" altrove" ) :}$
dove, come nel caso della traccia iniziale $mathcal(D)={(x,y) in RR^2:1<X<2,0<Y<X-1}$
...e proviamo a calcolare $mathbb{P}[Y<=1/4|X=3/2]$
Il primo approccio è sfruttando la definizione di probabilità condizionata (poniamo $0<=epsilon<=1/4$):
$mathbb{P}[Y<=1/4|X=3/2]=(2int_(0)^(1/4)dyint_(3/2-epsilon)^(3/2+epsilon)dx)/(int_(3/2-epsilon)^(3/2+epsilon)2(x-1)dx)=epsilon/(6epsilon-4epsilon)=1/2$
Il secondo e più naturale approccio consiste nell'integrare direttamente la densità condizionata
$int_(0)^(1/4)f_(Y|X)(y|x)dy$ dato $X=3/2$ ottenedo subito
$1/(x-1)int_(0)^(1/4)dy=1/(3/2-1)1/4=1/2$
cvd.....
- tieni presente che la variabile $X=(X_1,X_2)$ è un vettore aleatorio e la sua densità è uniforme. Ciò significa che la densità è l'altezza (costante) del mezzo parallelepipedo con base triangolare il cui volume è ovviamente 1 (da cui $f_(X_1X_2)*1/2=1 rarr f_(X_1X_2)=2$) e rappresenta tutta la distribuzione di probabilità del vettore ↑
- tommik
- Moderatore

- Messaggio: 4694 di 11278
- Iscritto il: 23/04/2015, 13:13
- Località: Cassano Magnago
5 messaggi
• Pagina 1 di 1
Torna a Statistica e probabilità
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite