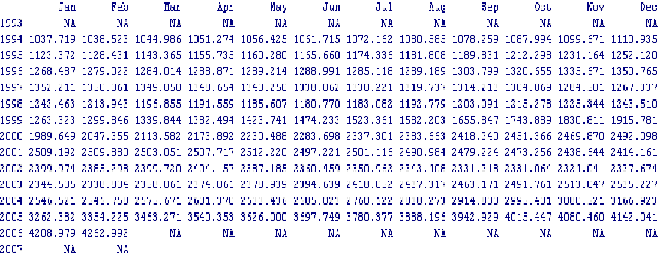
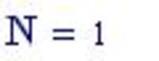Nell'approccio classico delle serie storiche si assume che i valori rilevati siano il risultato del comportamento congiunto di più componenti elementari individuabili attraverso opportune tecniche. A tale approccio sono state mosse numerose critiche, dal momento che non sempre risulta immediato individuare le componenti elementari e fornirne un'interpretazione.
Lo scopo dell'analisi classica delle serie temporali è quindi quello di scomporre la serie nelle sue componenti elementari per poterle studiare meglio.
Le componenti di una serie storica di solito sono le seguenti: trend, stagionalità, ciclicità, residuale.
Yt=Tt + St + Ct + Et,
dove le componenti sono espresse in termini assoluti, oppure in modo moltiplicativo:
Yt=Tt * St * Ct * Et,
in cui il trend Tt è espresso in termini assoluti, mentre le altre componenti sono espresse come fattore di proporzionalità rispetto a Tt.
La componente trend definisce l'andamento di lungo periodo della variabile e può essere definita come quella tendenza a crescere, a decrescere o a rimanere costante che un fenomeno manifesta in un lungo arco di tempo. La componente stagionale riguarda le dinamiche temporali con fase, periodo e ampiezza fissa tipica di serie storiche infrannuali, mentre il ciclo è tipico di serie storiche che descrivono fenomeni economici in un periodo di osservazione piuttosto lungo. La componente residuale racchiude fattori di natura erratica che influenzano il fenomeno in maniera casuale.
Per proseguire nell'analisi con R occorre implementare il pacchetto ast:
> "library(ast)"
[1] "library(ast)"
Stima delle componenti: Metodo delle medie mobili
Per la stima della componente trend i metodi più utilizzati sono: la perequazione meccanica con medie mobili e l'applicazione dell'operatore differenza.
Il metodo delle medie mobili consente di individuare l'andamento di lungo periodo della serie, eliminando l'influenza delle variazioni di breve periodo. Occorre determinare in maniera esatta il numero dei termini da perequare. Il pacchetto ast mette a disposizione la funzione filter():
> xt.filt
il parametro filter viene fissato al valore corrispondente ad una serie mensile.
Si visualizzi la serie storica depurata:
> xt.filt
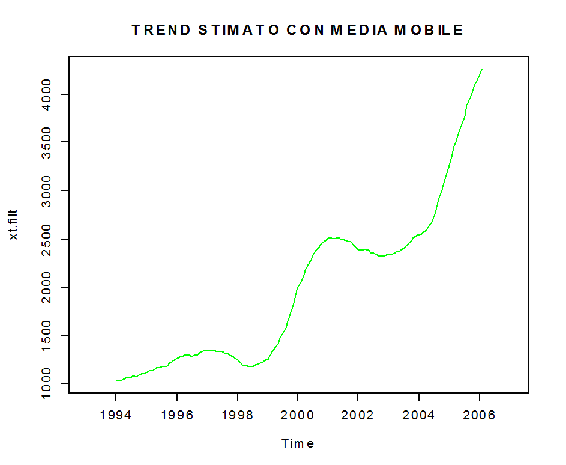
E' stata applicata ai dati originari una media mobile ponderata a 13 termini per eliminare la stagionalità e mettere in risalto solo la componente di fondo. Per ottenere una visualizzazione grafica:
> plot(xt.filt,main="TREND STIMATO CON MEDIA MOBILE",col="green")
Metodo delle differenze
Un ulteriore metodo per eliminare il trend è quello di operare sulle differenze tra i termini della serie storica: le differenze del primo ordine rimuovono un trend lineare, quelle del secondo ordine un trend parabolico, quelle di ordine k rimuovono un trend polinomiale di grado k.
Il comando di R per applicare tale metodo è diff.ts()
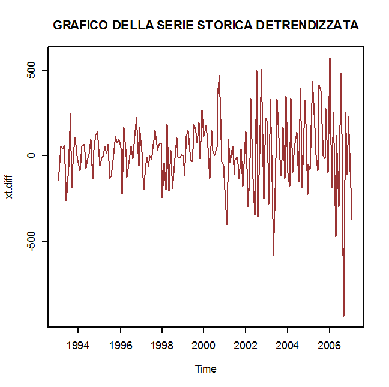
> xt.diff
Si visualizzi la serie storica differenziata
> xt.diff
Si riporta il grafico della serie storica detrendizzata:
> plot(xt.diff,main="GRAFICO DELLA SERIE STORICA DETRENDIZZATA",col="brown")
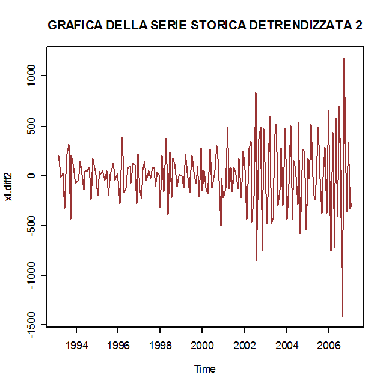
Usando in maniera ripetuta il comando diff.ts() si ottengono le differenze di qualsiasi ordine. Ad esempio la differenziazione del secondo ordine porta ai seguenti risultati:
> xt.diff2> plot(xt.diff2,main="GRAFICA DELLA SERIE STORICA DETRENDIZZATA 2",col="brown")