L'approccio moderno o stocastico (contrapposto a quello classico o deterministico) si basa sul concetto mutuato dal calcolo delle probabilità di processo stocastico.
Definiamo il processo stocastico come una famiglia (o successione) di variabili aleatorie Xt(W) definite sullo stesso spazio degli eventi W e ordinate secondo un parametro t (appartenente allo spazio parametrico T) che nell'analisi delle serie storiche è il tempo. In questo modo la serie storica può considerarsi come una
realizzazione campionaria finita del processo stocastico.
Applichiamo questi concetti alla serie dei residui standardizzati stimati con il metodo stl() contenuti nel vettore res.stl.
> mean(res.stl)
[1] 0.6746644
> var(res.stl)
[1] 21613.9
Per quanto riguarda le funzioni di autocovarianza e di autocorrelazione si usa il comando acf() che permette di ottenere il correlogramma o il grafico delle autocovarinaze oppure la semplice stampa delle autocovarianze o dei coefficienti di autocorrelazione:
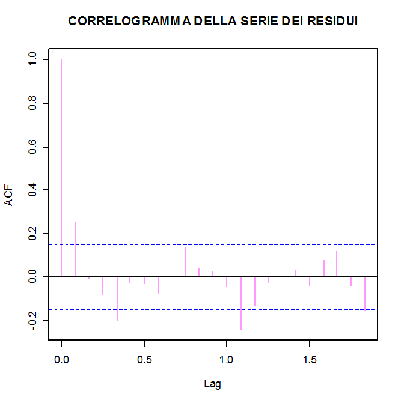
> acf(res.stl,type="correlation",plot=TRUE,main="CORRELOGRAMMA DELLA SERIE DEI RESIDUI",col="violet")
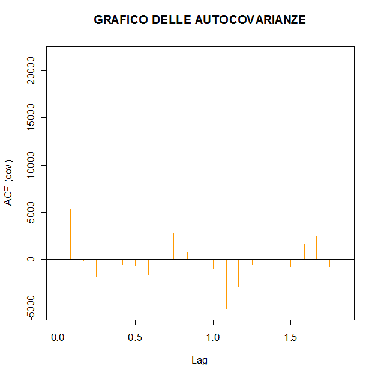
> acf(res.stl,type="covariance",plot=TRUE,main="GRAFICO DELLE AUTOCOVARIANZE",col="orange")
I principali argomenti di acf(), oltre alla serie storica, sono type, con il quale ci specifica se si vogliono calcolare le autocovarianze (type=”covariance”) o i coefficienti di correlazione type=”correlation”) e plot che serve per indicare se tracciare il grafico (plot=TRUE) che è il valore di default oppure se stampare l'output (plot=FALSE)
> acf(res.stl,type="correlation",plot=FALSE)
Autocorrelations of series 'res.stl', by lag
0.0000 0.0833 0.1667 0.2500 0.3333 0.4167 0.5000 0.5833 0.6667 0.7500 0.8333
1.000 0.251 -0.007 -0.087 -0.204 -0.026 -0.030 -0.077 0.004 0.134 0.042
0.9167 1.0000 1.0833 1.1667 1.2500 1.3333 1.4167 1.5000 1.5833 1.6667 1.7500
0.029 -0.046 -0.242 -0.135 -0.027 0.004 0.033 -0.038 0.080 0.118 -0.040
1.8333
-0.156
che fornisce i lag e i corrispondenti coefficienti di autocorrelazione o le autocovarianze. Con il comando acf() è possibile stimare anche i coefficienti di correlazione parziale specificando l'argomento type=”partial”. Analogo risultato si ottiene con il comando pacf().
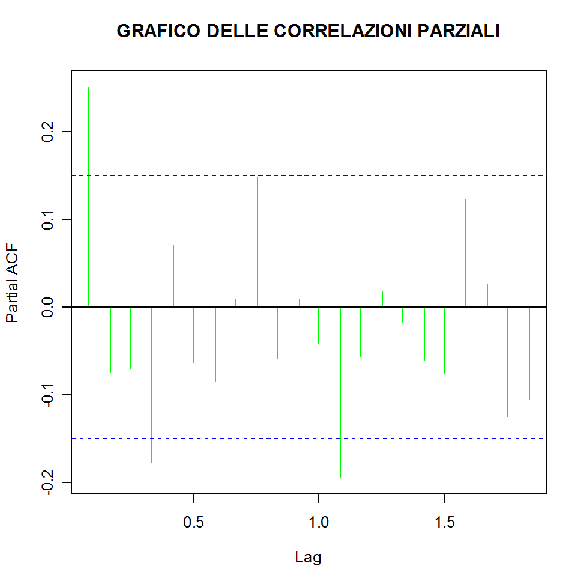
La correlazione ρ(k) tra dati distanti k lag è influenzata dalle relazioni lineari con i dati intermedi. La funzione di autocorrelazione parziale p(k) misura la correlazione tra xt e xt+k dopo che sia stata eliminata la parte “spiegabile linearmente” da xt+1, xt+2, . . . , xt+k-1 .
> pacf(res.stl,plot=TRUE,main="GRAFICO DELLE CORRELAZIONI PARZIALI",col="green")
> pacf(res.stl,plot=FALSE)
Partial autocorrelations of series 'res.stl', by lag
0.0833 0.1667 0.2500 0.3333 0.4167 0.5000 0.5833 0.6667 0.7500 0.8333 0.9167
0.251 -0.075 -0.071 -0.177 0.071 -0.064 -0.085 0.009 0.149 -0.059 0.010
1.0000 1.0833 1.1667 1.2500 1.3333 1.4167 1.5000 1.5833 1.6667 1.7500 1.8333
-0.042 -0.194 -0.057 0.020 -0.018 -0.062 -0.076 0.124 0.027 -0.125 -0.105