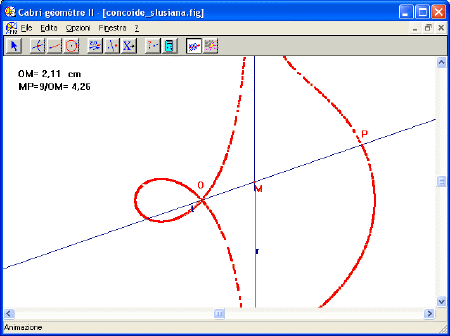
La concoide slusiana con Cabri
ROBERTO MANNI

Cabri G�om�tre simula una pagina di quaderno su cui � possibile disegnare figure geometriche con le quali interagire nei modi specificati dal programma stesso. Il software, semplice ed intuitivo nell�utilizzo, rivela notevoli potenzialit� nelle costruzioni geometriche.
Cabri, a mio avviso, potrebbe addirittura diventare un valido strumento didattico anche nell�ambito universitario se affiancato al classico studio di quella parte di programma dedicata alle curve algebriche in un corso di Geometria o, perch� no, di Matematiche Complementari, in cui si voglia dare il giusto risalto anche all�aspetto della costruzione che porta al disegno della curva e successivamente alla sua equazione.
A tal proposito ho voluto provare ad elaborare con Cabri G�om�tre la costruzione di una cubica circolare: la concoide slusiana.
Ho ricavato la costruzione di questa curva dal testo di Gino Loria �Curve piane speciali algebriche e trascendenti�, di cui mi piace citare il seguente passo relativo:

Fra le particolari cubiche circolari ve n�ha una che sfugg� all�attenzione dei geometri moderni sino al giorno in cui venne pubblicato il carteggio tra R. de Sluse e C. Huygens . La chiameremo Concoide slusiana e la definiremo come segue: Dato un punto O, una retta r ed una costante k², si conduce per O una trasversale arbitraria a tagliare r in M e si porta su OM a partire da M, dalla parte opposta a quella dove sta O, un segmento MP tale che OM ∙ MP = k²; il luogo di P sar� una concoide slusiana .

In un opportuno sistema di riferimento cartesiano, l�equazione della curva � a(x � a)(x² + y²) = k² x², dove si � indicata con a la distanza tra O ed r.

1. [punto] disegnare un punto

2. [nomi] assegnare al punto il nome O

3. [retta] disegnare una retta che non passi per O

4. [nomi] assegnare alla retta il nome r

5. [retta] disegnare una retta passante per O e che intersechi la retta r

6. [nomi] assegnare alla retta il nome t

7. [intersezione di due oggetti] segnare il punto di intersezione delle rette r e t

8. [nomi] assegnare il nome M al punto di intersezione

9. [distanza e lunghezza] calcolare la lunghezza del segmento OM

10. [calcolatrice] calcolare 9/OM (si � scelto k=3 ma si pu� scegliere un altro valore di K) disporre in un punto del foglio il risultato del calcolo

11. [semiretta] con origine M e disposta su t dalla parte opposta a O

12. [trasporto di misura] indicare la semiretta e il valore ottenuto con la calcolatrice

13. [nomi] assegnare al punto ottenuto il nome P

14. [traccia] indicare il punto P

15. [puntatore] muovi la retta t

L'applet seguente � interattiva ma non lascia la traccia. Doppio clic sull'applet per attivare la barra dei comandi, dalla quale puoi vedere la costruzione passo passo e scaricare la figura.