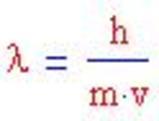Possibile fare a meno delle onde di de Broglie?

In questo articolo si fa riferimento a quanto già sostenuto in [1, Paragrafo 4.7] e, in più, si propone un modello delle particelle che esclude il modello di de Broglie che associa ad ogni particella un'onda. Si sostiene, invece, che ogni particella, in particolare l'elettrone, sia un corpuscolo non perfettamente sferico (con superficie ondulata?), in modo da poter giustificare gli stessi risultati ottenuti con le classiche esperienze che sono portate a conferma del modello di de Broglie.

Non c'è più bisogno, quindi, di fare riferimento al principio d'indeterminazione e a quello di complementarietà.

Si tratta, ora, di tradurre questa proposta in un solido modello
matematico che possa fare delle previsioni quantitative in accordo con i dati sperimentali. Sempre che i giovani fisici capaci di farlo non incontrino lo stesso ostracismo incontrato da altri da 90 anni a questa parte. Infine viene proposto di ripetere l'esperienza di Merli, Missiroli e Pozzi in camera a nebbia o similare, per confermare l'ipotesi che il singolo elettrone segua una traiettoria ben precisa, contro l'interpretazione diffusa di Copenhagen.

Il modello ondulatorio delle particelle di de Broglie ha avuto notevoli successi sia con esperienze dirette che ne hanno confermato la validità (ad esempio le esperienze di Davisson e Germer del 1927 e quelle più recenti che hanno utilizzato il microscopio elettronico sulla diffrazione e l'interferenza degli elettroni) sia per le numerose conferme indirette derivate dalla meccanica ondulatoria di Schrödinger e dalla meccanica quantistica in generale. Tutto questo ha impedito di cercare di interpretare certi risultati sperimentali utilizzando modelli interpretativi diversi¹.

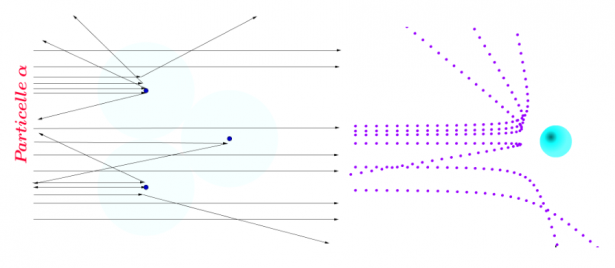
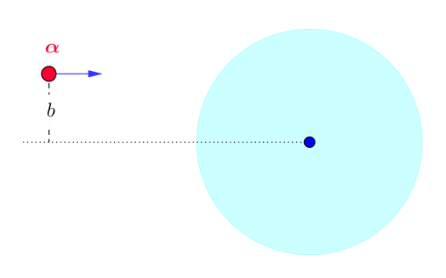
Ad esempio, facendo riferimento all'esperienza di Rutherford per stabilire il modello nucleare dell'atomo, bisogna considerare il parametro d'urto, in funzione del quale le particelle alfa subiscono deviazioni più o meno grandi fino a 180 (urto centrale e rimbalzo all'indietro). Tutto ciò è schematizzato nelle figure 1, dove la diversa deflessione delle particelle alfa è data dal valore diverso del parametro d'urto b, il cui significato viene specificato in figura 2.

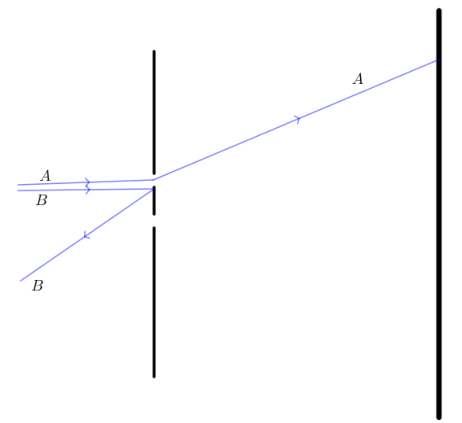
Ora tutte le esperienze sulla diffrazione e l'interferenza degli elettroni fanno riferimento ad un fascio di elettroni (o anche, recentemente, ad un singolo elettrone) che colpiscono una fenditura o due fenditure o un reticolo di cristalli, suppo nendo di avere un fascio rigorosamente monocinetico (tutti gli elettroni con la stessa velocità) e ben collimato di elettroni! Ma questo in laboratorio non lo si ha mai, per quanto si possano usare tutti gli accorgimenti per avere un fascio il più possibile collimato di elettroni tutti con la stessa velocità! E questo per il meccanismo stesso con cui si ottiene il fascio (ad esempio filamento di tungsteno portato ad incandescenza che emette elettroni successivamente accelerati e collimati con opportuni campi elettrici e magnetici).

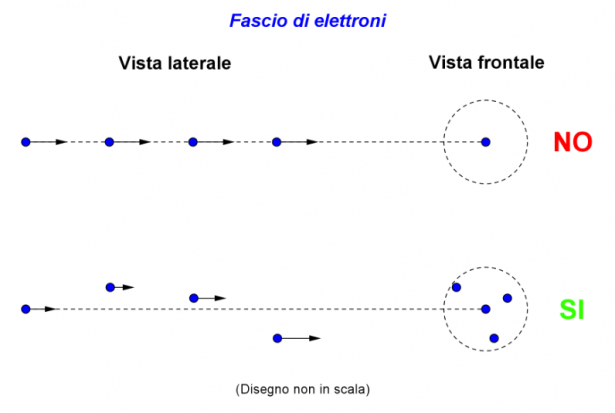
Guardando la figura 3 ci si rende conto subito che la situazione rappresentata in alto (tutti gli elettroni perfettamente allineati e con la stessa velocità) non è quella ottenibile in laboratorio, quella in basso sì (dove il fascio di elettroni realmente ottenuto avrà comunque una certa dispersione sopra e sotto la direzione teorica immaginata)² Allora ciascun elettrone del fascio, normalmente, ha un proprio parametro d'urto, diverso da quello degli altri elettroni. Quindi subisce dai bordi della fenditura o delle fenditure deviazioni differenti sia per il parametro d'urto differente sia per la velocità differente. Infine, invece di sostenere, come si fa con de Broglie dal 1923, che all'elettrone o ad altra particella è associata un'onda con lunghezza d'onda

(

costante di Planck, massa della particella, velicità della particella), non avendo mai visto direttamente queste particelle, non si potrebbe supporre che le stesse invece di essere considerate puntiformi o perfettamente sferiche, abbiano una forma a simmetria sferica con supericie on dulata? In pratica invece di dire che alla particella è associata un'onda si dice che la particella non è puntiforme³ed ha una supericie sferica ondulata, come nella figura 4, dove il numero e la profondità delle 'protuberanze' sono solo esempliicativi⁴.
Sullo schermo che raccoglie questi elettroni si ha l'impressione che il risultato sia analogo a quello ottenuto con il modello matematico di un fascio di onde luminose! In tal modo una particella continua ad essere una particella e solo il comportamento collettivo di molte particelle (che hanno approssimativamente la stessa velocità e parametri d'urto leggermente diversi) dà l'impressione di essere di fronte ad una particella-onda. In più si potrebbe dire che se la diversità del parametro d'urto (e del valore della velocità dei singoli elettroni) contribuisce ad avere una banda larga delle tracce degli elettroni, il fatto che la supericie degli elettroni sia ondulata contribuisce alla formazione delle righe sullo schermo (le particelle rimbalzano con le loro protuberanze contro i bordi delle fenditure). Non risulta che un modello del genere sia mai stato sottoposto ad approfondimento dal punto di vista matematico anche se, forse, molto diffcile da effettuare. In fondo l'ipotesi di de Broglie costituisce la base di un modello che funziona. Ma non è detto che sia l'unico! Forse qualche giovane fisico volenteroso (che sopravvive a tutte le censure in vigore da 90 anni per la difesa dell'interpretazione di Copenhagen) potrebbe ottenere qualche risultato utile tenendo presente quanto qui esposto.

Nel settembre 2012 la rivista Physics World lanciò un sondaggio per decretare l'esperimento più bello della fisica. Vinse un esperimento di interferenza da due fenditure di un fascio di elettroni, con passaggio, come sostengono gli autori, di un elettrone alla volta. Tale esperienza è stata eseguita a Milano nel 1974 da tre giovani scienziati italiani dell'Università di Bologna: Merli, Missiroli e Pozzi, che ottennero unaf igura d'interferenza lasciata dagli elettroni su una lastra sensibile come nella Figura 5:

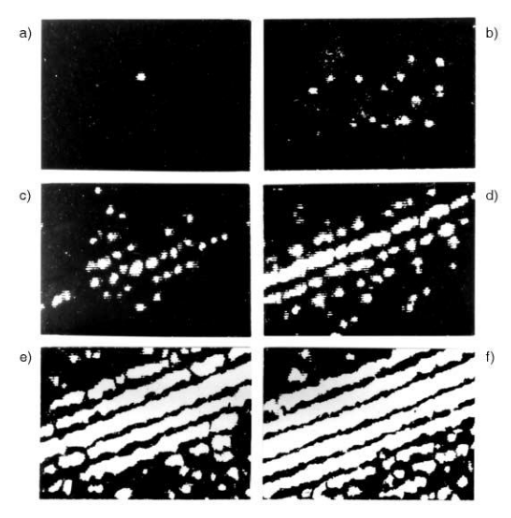
Gli autori che ottennero la Figura 5 così commentarono i loro risultati:

Si può quindi concludere che il fenomeno del l'interferenza è conseguenza solo del l'interazione dell'elettrone singolo con l'apparato sperimentale. A questo punto, per interpretare le frange d'interferenza possiamo pensare che si veriichi l'una o l'altra di queste condizioni:

a) L'elettrone cessa di essere una particella e si distribuisce con continuità nello spazio in modo analogo ad un'onda;

b) l'elettrone è una particella che arriva in un punto ben definito dello schermo impressionando un singolo grano dell'emulsione fotografica e la figura d'interferenza è il risultato statistico di un gran numero di elettroni. ... gli elettroni arrivano sullo schermo come se fossero particelle, ma la loro probabilità di arrivo è determinata da una curva che ci è nota nello studio dei fenomeni d'interferenza della luce, ove rappresenta la distribuzione dell'intensità luminosa. È in questo senso che gli elettroni si comportano come onde [3, p.94, neretto RS].

Nella citazione riportata non viene esclusa l'interpretazione statistica del comportamento degli elettroni-particelle, non dando affatto per scontata l'interpretazione degli elettroni come onde. Interpretazione che sembrerebbe prevalere dal filmato realizzato per spiegare le varie fasi dell'esperimento (https://www.youtube.com/watch?v=tMl9Me2hoLE). Infatti, trascrivendo quanto affermato verso la conclusione del filmato, gli autori dello stesso affermano:

[...] Il comportamento dell'elettrone può essere rappresentato da un'onda . . . Quello che si osserva è il risultato statistico di un grande numero di eventi. L'immagine che osserviamo sullo schermo rappresenta la somma di un grande numero di eventi indipendenti ciascuno dei quali rappresenta l'interazione di un singolo elettrone con l'apparato sperimentale.

dove la prima affermazione (preceduta da un altra in cui si dice che l'elettrone-onda è un modello che può spiegare la figura finale osservata) può sembrare in contrasto con il resto della citazione.

Come potrebbe sembrare in contrasto anche quest'altra citazione dall'articolo:

Le frange d'interferenza (ed anche quelle di diffrazione) non sono pertanto dovute al fatto che l'elettrone si ditribuisce con continuità nello spazio e diventa un'onda (infatti in questo caso avremmo dovuto avere delle frange d'intensità decrescente al decrescere dell'intensitò della corrente). l'elettrone si manifesta come una particella la cui interazione con l'apparato sperimentale. . . dà luogo ad una distribuzione spaziale descrivibile matematicamente tramite un'onda. . . . In conclusione gli elettroni arrivano sullo schermo come se fossero particelle, ma la loro probabilità di arrivo è determinata da una curva che ci è nota dai fenomeni d'interferenza della luce, ove rappresenta la distribuzione del l'intensità luminosa. È in questo senso che gli elettroni si comportano come onde. [3, p.96].

Dunque una semplice analogia.

In effetti, guardando con attenzione le figure parziali (da a a f ) della figura 5, si vede chiaramente, specie in a e in b, che all'inizio si hanno delle indicazioni precise su dove sono andati a sbattere gli elettroni, che, dunque, hanno seguito una traiettoria ben precisa. Niente onda associata ai primi elettroni che arrivano sullo schermo. Per gli elettroni che arrivano successivamente non v'è ragione di supporre un comportamento diverso. Solo successivamente, all'aumentare nel tempo del numero degli elettroni che sbattono sullo schermo, comincia a intravedersi la forma (pattern) di una tipica figura d'interferenza. Ma questa è dovuta solo all'effetto statistico del gran numero di elettroni che cadono sullo schermo, ciascuno dei quali segue una traiettoria diversa come conseguenza del modello qui proposto nelle figure 3 e 4. Quindi, fermo restando che, comunque, la figura è l'effetto di un numero molto grande di elettroni (anche se passano uno alla volta), la stessa figura si può pensare ottenuta supponendo gli elettroni aventi la forma qui proposta. Forma che toglie l'ambiguità e il paradosso che gli elettroni possano passare contemporaneamente dalle due fenditure: gli elettroni passano da una sola fenditura, anche se non possiamo sapere da quale!

A conferma di quanto appena detto, si può evidenziare che, ripetendo lo stesso esperimento più volte nello stesso luogo o in luoghi diversi, si ottiene sempre la stessa figura d'insieme d'interferenza. Stessa figura solo d'insieme, in quanto, se ingrandiamo diverse volte la figura ottenuta, la posizione dei singoli elettroni che hanno lasciato la traccia non è sempre la stessa; il che signiica che si tratta solo di un comportamento statistico di un gran numero di elettroni. D'altra parte, nelle esperienze di urto fra particelle elementari, è possibile vedere con tecniche opportune (tipo camera a nebbia) se non la traiettoria della(e) particella(e), l'effetto del passaggio delle stesse. E dalle traccie trovate si tirano diverse conclusioni: natura della particella, tipo di carica, massa . . . . A questo proposito perchè non ripetere l'esperienza di Merli, Missiroli e Pozzi in una camera a nebbia (o a scintillazione o a bolle)? Dovrebbe essere possibile (almeno all'inizio) vedere le scie dei primi elettroni che lasciano una traccia sulla lastra! Certo ci saranno degli elettroni spuri che interagiscono con il mezzo, ma non sarà diffcile non tenerne conto, come in figura 6⁵. Non credo che l'esperimento sia di diffcile realizzazione. La cosa più diffcile sarà certamente trovare i fondi per la realizzazione dello stesso, visto che i programmi di ricerca sono sempre controllati dai soliti affezionati della scuola di Copenhagen!

Dunque il contrasto di fondo fra i diversi punti di vista riguardanti la meccanica quantistica si è spostato non sui suoi risultati universalmente accettati (anche da Einstein che era molto critico nei confronti dell'interpretazione di Copenhagen) ma sul fatto che questi risultati si applicano a una particella singola o, mediamente, a un insieme macroscopico di particelle dello stesso tipo. Fermo restando che non si può prendere un elettrone con una pinzetta, piazzarlo in un determinato punto e osservare, cosa succede quando lo si investe con un fascio di luce o altro, alcuni fisici (contrariamente a quanto sostiene la scuola di Copenhagen), sono favorevoli alla seconda ipotesi. In effetti, negli ultimi anni sono sorti alcuni studi seri e completi che hanno seguito questa strada alternativa, pur avendo gli stessi risultati dell'interpretazione ortodossa della meccanica quantistica, quella di Bohr e Heisenberg. Si citano, a questo proposito solo due articoli:

• L.E. Ballentine, The Statistical Interpretation of Quantum Mechanics, Reviews of Modern Physics, vol. 42, n. 4, 1970, pp. 358-381 (Lo stesso autore ha successivamente scritto un corposo manuale sulla meccanica quantistica, dal titolo Quantum Mechanics: A Modern Development, World Scientiic Publishing, 1998, avendo come come linee guida quanto scritto nell'articolo citato);
• U. Klein, The Statistical Origins of Quantum Mechanics, Physics Research International, vol. 2010, Article ID 808424, 18 pages, 2010.

rinviando alla vasta letteratura qui riportata per ulteriori approfondimenti.

Bisogna dire che lo stesso de Broglie, già nel 1927, diede un'interpretazione diversa della sua ipotesi, pensando alla doppia soluzione o all'onda-pilota di cui la particella è una singolatità. Ma presto rinunciò a difendere la sua idea giovanile, si adeguò alla maggioranza (la scuola di Copenhagen), per ritornare sull'onda pilota solo nel 1952. Il modello qui proposto (la particella elementare sferica con supericie ondulata) potrebbe portare un ulteriore sostegno a tutte le interpretazioni statistiche della meccanica quantistica, che non deve interdersi applicata ad una singola particella, ma ad numero enorme di particelle dello stesso tipo.

Bisogna accompagnare questo modello intuitivo con un adeguato modello matematico da cui poter dedurre risultati quantitativi compatibili con i risultati sperimentali. Si spera che questo modello riesca ad interpretare la realtà fisica meglio di quanto non ha fatto la meccanica quantistisca di Heinsemberg, Born, Jordan, Pauli. Quando si è arrivati a negare la realtà stessa fino ad affermare che l'unica cosa reale erano gli oggetti matematici della meccanica quantistica. Enrico Fermi, in una lettera del 1925, dopo che venne formulata la meccanica delle matrici da parte di Heinsemberg, all'amico Emilio Segré, scrisse:

La mia impressione è che il progresso di questi ultimi anni non sia stato molto grande. . . .Per il mio gusto, mi pare che comincino veramente ad esagerare nel la tendenza di rinunciare a capire le cose⁶.

E se lo diceva Fermi bisognava cominciare a preoccuparsene seriamente e innescare la retromarcia per non rinunciare a capire. La storia della Fisica, purtroppo, è andata diversamente.

In effetti la cosa resta diffcile per l'impossibilità teorica di riuscire a visualizzare le particelle elementari con metodi diretti, la luce, in quanto questa ha una lunghezza d'onda molto più grande del mondo degli atomi, dei nuclei atomici, degli elettroni e di altre particelle elementari: 10 volte più grande dell'atomo,

(cento milioni) di volte più grande del nucleo atomico, (cento miliardi) di volte più grande dell'elettrone. È come voler osservare un granello di sabbia usando un carro armato! Allora bisogna immaginare dei modelli matematici e da questi risalire, in modo indiretto, con esperienze opportune, ad avere indicazioni su come è e su come si comporta il mondo microscopico. Ma non si può affermare che l'unica cosa reale è la matematica del modello! Bisogna avere il coraggio di ammettere che, a questo livello della realtà, solo metodi statistici sono ammissibili, come si è fatto con la teoria cinetica dei gas, che ha consentito di avere indicazioni corrette, per quello che interessava, ad esempio sulla velocità media di una molecola di gas, usando un termometro e la matematica del modello del gas! Ma con questo non si è detto che le molecole non hanno realtà fisica (Beh, veramente, qualcuno questo all'inizio lo aveva anche detto!). Bohr nel 1927 enunciò il principio di complementarietà: la luce e le particelle possono avere un comportamento corpuscolare o ondulatorio; solo l'esperimento specifico che si vuole effettuare ci consente di scegliere il modello più appropriato; non si deve cercare oltre per determinare un unico comportamento!

Heisenberg, che è stato allievo di Bohr a Copenhagen, formulò nel 1925 la meccanica delle matrici e nel 1927 il principio d'indeterminazione; nel 1929 ebbe a dire che il quinto congresso Solvay a Bruxelles nel 1927 ha detto praticamente l'ultima parola sull'interpretazione della meccanica quantistica, quella secondo i canoni della scuola di Copenhagen. Al contrario il fisico francese Langevin, a proposito dello stesso congresso, affermò che 'la confusione delle idee raggiunse il suo massimo'⁷.

Bisogna dire che l'artificiosità e la complessità della meccanica quantistica ha raggiunto livelli incomprensibili, completamente distaccati dalla realtà fisica e ben aldilà di quanto avrebbe potuto immaginare lo stesso Heinsemberg! Non è pensabile né auspicabile che la natura, per quanto scritta in caratteri matematici (come diveva Galileo), possa aver raggiunto livelli di astrattezza tali che, molto spesso, solo i fisici che la hanno utilizzata o inventata per la prima volta siano i soli a comprendarla. E gli specialisti di un ramo della fisica non capiscono la matematica usata e sviluppata per altri rami della Fisica!

Per questo è necessario un grande gesto d'umiltà, ritornare a considerare le esperienze cruciali della fisica e tentare di interpretarle con modelli più semplici e intuitivi, dove la matematica usata non deve mascherare la semplicità con cui i diversi mattoni della realtà fisica si sono messi assieme per formare il mondo macroscopico che conosciamo!

È con questo spirito che si propone ora una semplice interpretazione di una grande esperienza cruciale della Fisica (da ripetere, come scritto, in una camera a nebbia o similare). Che va accompagnata da un opportuno modello matematico (semplice!), che possa spiegare l'esperienza stessa ed altre esperienze, a cominciare, per esempio, dallo spettro dell'atomo d'idrogeno! La proposta ai più potrà apparire ingenua e mettere il sorriso sulle labbra di molti. Ma la situazione attuale è insostenibile e irrealistica: bisogna trovare la strada maestra che permetta di evitare, non solo le onde di de Broglie, ma anche il bla bla filosoico sviluppato attorno al principio d'indeterminazione, al principio di complementarità, al libero arbitrio (?!?), alla fine del princpio di causalità, alla castrazione dei cervelli dei giovani fisici operata da Bohr e dalla sua scuola...

Resta l'ostracismo a qualunque interpretazione alternativa a quella di Copenhagen delle riviste specializzate, delle case editrici, dei professori inamovibili che occupano le cattedre di Fisica in tutto il mondo. Questo è un problema serio che va affrontato e superato, all'inizio mettendo in rete le proposte ritenute innovative anche su siti non specializzati dove non c'è nessuna censura: si spera in tal modo che qualche altro giovane fisico raccolga la sfida, diffonda la ricerca e porti il suo contributo. L'importante è rompere il muro di gomma che fa rimbalzare qualunque idea alternativa, aldilà del fatto che questa sia foriera di sviluppi positivi o no⁸.

È significativa la notizia, nel settembre 2011, della scoperta dei famosi neutrini superluminali da parte del gruppo OPERA al CERN di Ginevra: qui circa duecento tra scienziati conosciuti e giovani ricarcatori hanno dato in pompa magna (preceduti, il giorno prima, questa volta con velocità superiore a quella della luce, dal Prof. Antonino Zichichi) la notizia della scoperta. Allora, per motivi opposti a quelli della meccanica quantistica, tutti o quasi si sono precipitati sulla notizia avvalorandola, con dotte interviste su stampa, televisione, internet... L'autore di questo articolo, contro tutti o quasi, ha inviato una lettera a ben tre tra i maggiori quotidiani italiani per sostenere che la notizia era una bufala: la lettera non venne pubblicata e si preferì dare la parola a dottissimi professori universitari che avvaloravano la scoperta e decretavano, finalmente, la fine del principio di causalità (come esplicitamente affermato da A. Zichichi) anche nella teoria della relatività [1, Introduzione]⁹.

Altri professori-ricercatori si precipitarono a pubblicare articoli pieni di matematica (che tanto nessuno capiva) per avvalorare la scoperta e non perdere il treno della corsa all'oro. Peccato che lo stesso gruppo di ricercatori del CERN, qualche mese dopo, annunciò che la scoperta era fasulla in quanto i risultati da loro trovati non erano corretti (un cavo era stato avvitato male!). Certo che la notizia ha annebbiato la vista ed il cervello di molti addetti ai lavori perchè da un grafico come quello della figura 7 emerge subito che, crollando la Meccanica Relativistica, sarebbe crollata tutta la Fisica!

Con la meccanica quantistica, invece, finora, è prevalso il principio di precauzione infinita. Allora largo ai giovani per sfondare il muro di gomma. Con un incoraggiamento sfacciato, anche economico, per quei giovani fisici che vogliono aprire nuove vie, anche se queste possono sembrare incerte e poco promettenti. Fu così anche per la nascita della meccanica quantistica, per cui ci sono voluti quasi 30 anni, dal 1900 al 1927, ed il lavoro di tanti fisici come Planck, Einstein, Bohr, de Broglie, Schrödinger, Born, Heinsenberg, Pauli, Jordan, Dirac prima che assumesse la veste deinitiva che si è imposta negli anni successivi, fino ad oggi.

Ma fu proprio Dirac, nel 1975, a scrivere:

[...] Penso che potrebbe benissimo trovarsi che, inalmente, Einstein abbia avuto ra gione, perché la forma attuale del la meccanica non dovrebbe essere considerata deini tiva. Esistono grandi diffcoltà con la meccanica quantistica attuale. È il meglio che ino ad ora si possa fare. Ma non bisogna credere che questo possa durare per sempre. Penso molto verosimile che, in futuro, potremo ottenere una meccanica quantistica migliorata, in cui ci sarà il ritorno al determinismo, ciò che, di conseguenza, giustiicherà il punto di vista di Einstein^10.

Ancora Dirac, già nel 1930 [5, pp. XII-XIII. Neretto RS.], metteva in guardia contro la perdita dell'intuizione fisica a favore del formalismo matematico:

L'essenza del nuovo metodo del la fisica teorica sta nello sviluppo dell'uso della teoria delle trasformazioni, applicata prima alla relatività e successivamente alla teoria quantistica. Ulteriori progressi stanno nella direttiva di rendere le nostre equazioni invarianti per trasformazioni sempre più generali. Questo stato di cose è assai soddisfacente da un punto di vista filosoico, poiché implica un crescente riconoscimento della parte rappresentata dall'osservatore nell'introdurre egli stesso le regolarità che appaiono nelle sue osservazioni, e una mancanza di arbitrarietà nelle vie della natura, ma rende meno facili le cose per lo studioso di fisica... i nuovi concetti della fisica possono essere acquisiti solo attraverso una lunga familiarità con le loro proprietà e i loro usi... la matematica è solo uno strumento, ed è bene imparare a impadronirsi delle idee fisiche senza fare riferimento alla forma matematica. In questo libro ho cercato di lasciare in primo piano la fisica...

Conclusione

La proposta qui presentata è volutamente provocatoria (anche perchè senza una sola prova quantitativa), vuole solo spingere i giovani a provare sentieri nuovi e, soprattutto, a cercare modelli causali o almeno a seguire interpretazioni statisticamente causali della meccanica quantistica (come sostenuto in [1, paragrafo 4.10]). La causalità non deve essere abbandonata: in qualunque ricerca scientiica, degna di questo nome, deve essere il filo conduttore. Altrimenti si può lasciare la scienza ai maghi, ai religiosi-shamani (di qualunque religione), ai prestigiatori! Il modello dell'atomo d'idrogeno di Bohr è stato un

autentico colpo da mago: ispirate dalla formula empirica di Balmer e dall'esistenza della costante di Planck, le ipotesi contradittorie¹¹ di Bohr (1913) erano completamente campate in aria (il coniglio dal cappello del mago) che solo con le onde di de Broglie (1923-24) hanno trovato una parvenza di giustiicazione teorica. Dopo è arrivata la Scuola di Bohr a Copenhagen, dov'è cominciato il lavaggio dei cervelli dei giovani ficici, come affermò il premio Nobel per La Fisica (1969) Murray Gell-Mann, e 'bonjour les dégã¢ts'! La Fisica dovrebbe fare a meno dei cosiddetti 'dualismi' (che vanno bene, forse, solo in Filosoia). Bisognerebbe evitare non solo le onde associate alle particelle (de Broglie), ma anche le particelle associate alle onde (Planck, Einstein). Dunque una sana rifondazione dovrebbe ripartire proprio da una rianalisi accuratissima delle esperienze fondanti: corpo nero, effetto fotoelettrico, effetto Compton..., evitare la cosiddetta Fisica del le pulci (salti quantici), non confondere il comportamento collettivo di un insieme di particelle uguali con quello di una singola particella!

Per contattare l'autore: raffaele.sntoro@yahoo.it

References

• [1] Santoro R., La Relatività e la Fisica contemporanea - Dal le favole sui neutrini superluminali alla realtà delle onde gravitazionali, RSEdizioni (Amazon), 2017.
• [2] Bacciagaluppi G., Valentini A., Quantum Theory at the Crossroads - Reconsidering the 1927 Solvay Conference, Cambridge University Press.
• [3] Merli P.G., Missiroli G.F., Pozzi G., Diffrazione e interferenza di elettroni. II: Interferenza, Giornale di Fisica, 2, 1976
• [4] Segré, E., Enrico Fermi, fisico: una biografia scientifica, Zanichelli, Bologna, 1971
• [5] Dirac Paul A.M., I Principi della Meccanica Quantistica, Serie di Fisica, Boringhieri, 1959

---

Note

1. In reality, there was the model of the double solution or the pilot-wave (de Broglie 1923-1927, taken up by de Broglie himself and by D. Bohm in 1952), but was not very successful. On the contrary, it has undergone various ostracisms, such as the one reported in [2, pp. 248-9]
2. La stessa cosa si potrebbe dire delle esperienze effettuate con la luce, considerando il modello corpuscolare, a fotoni, della stessa.
3. Non si capisce perchè, pur affermando che le particelle abbiano dimensioni che variano nell'intervallo (10^{-15}m - 10^{-18} m) debbano essere considerate puntiformi. Sono piccolissime, ma non puntiformi ed alla loro scala di grandezza potrebbero benissimo avere una forma non perfettamente sferica.
4. Ovviamente potrebbe essere qualunque altra cosa che violi la perfetta simmetria sferica. Intanto un aiutino in questa direzione viene già dal fatto che l'elettrone, ad esempio, ha un suo momento magnetico intrinseco che potrebbe avere la sua influenza in esperienze tipo il passaggio di elettroni attraverso due fenditure. Ricerche sono in corso per scoprire se ci sia anche un momento di dipolo elettrico. Singolarmente o combinati questi momenti intrinseci potrebbero interagire con l'apparecchiatura e fornire, statisticamente, i risultati osservati.
5. Qui certamete sarà possibile dare una risposta all'annosa questione: elettrone-onda o elettrone-particella con traiettoria asssociata.
6. [4], p. 209. Neretto RS.
7. Circostanza riportata in [2]
8. Negli ultimi ottantanni quanti articoli di ricerca, che non hanno avuto nessuna storia o citazione, sono stati pubblicati? Non so se esiste una statistica a questo riguardo, ma certamente la percentuale sarà molto alta. Moltissimi ricercatori che hanno pubblicato tali articoli hanno anche fatto carriera nelle Università di tutto il mondo!
9. Bisogna dire che il blog del isico delle particelle Marco Delmastro, al link http://www.borborigmi.org/2011/09/23/considerazioni-dopo-il-seminario-di-opera-ovvero-di-come-si-misura-la-velocita-dei-neutrini-superluminali-o-meno/ riportando anche dei dubbi espressi da qualcuno circa l'affdabilità dell'errore misurato, ha fatto le pulci al metodo usato in tre punti fondamentali: misura della distanza, misura del tempo di percorrenza, stima dell'errore. Qualcuno dei collaboratori di OPERA si è riiutato di irmare l'articolo. Ma la corsa all'oro dei teorici cominciò lo stesso come ebbe a prevedere Carlo Cattaneo nel suo blog della rivista Le Scienze: '... qualcuno scommette che lunedì ci sarà un profluvio di preprint teorici? per cui passerà alla storia come l'international crackpotter day? per tentare di far calzare la teoria a un risultato ancora molto discusso.'!
10. P.A.M. Dirac, Direction in Physics, H. Hora and J.R. Shepanski, ed., Wiley, Sidney, 1976, p. 10. Citato, in francese (e da RS tradotto in italiano) dal prof. Franco Selleri, Le grand débat de la théorie quantique, Flammarion, 1994, p. 256. Neretto di RS.
11. L'elettromagnetismo classico vale per determinare le orbite 'consentite' dell'elettrone ma, al contempo, non vale perchè l'elettrone sulle orbite consentite, pur accelerando, non irradia energia elettromagnetica e non collassa.