_antoniobernardo
di _antoniobernardo
(90 punti)
8' di lettura
3 / 5 (5)
Lo scopo di questi appunti è quello di misurare il volume del contenuto di una cisterna cilindrica, quando siano note le sue dimensioni. Dimostreremo la formula ottenuta e ne vedremo un esempio applicativo.

Il problema della cisterna

Talvolta, sia nelle applicazioni pratiche che negli esercizi scolastici, può capitare di imbattersi nel problema del calcolo del volume contenuto in una cisterna. Le cisterne sono contenitori utilizzati per contenere principalmente acqua, per la cucina o per l'irrigazione o altri liquidi, come ad esempio il gasolio per riscaldare una casa.

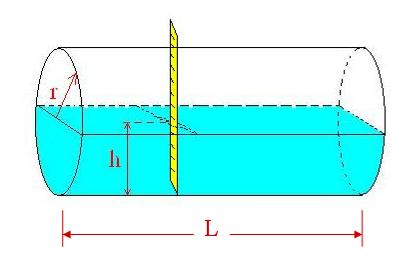
Le forme delle cisterne sono spesso riconducibili a quelle di solidi geometrici, il più delle volte sono sferiche oppure cilindriche.

Quando sono di forma cilindrica, sono poste spesso in orizzontale, come nella figura in basso. Affinché si possa pervenire ad un calcolo corretto del volume contenuto nella cisterna, occorre conoscere l'altezza h raggiunta dal liquido, il raggio di base r del cilindro e la lunghezza del cilindro, che indichiamo con L.

La formula per il calcolo del volume del liquido contenuto in una cisterna

In questo paragrafo enunciamo e dimostriamo la formula necessaria per il calcolo del volume del liquido contenuto all'interno di una cisterna.

La formula da utilizzare è:

[math]V = L \cdot [ \frac{ \pi \cdot r^2}{2}+r^2 \cdot \arcsin (\frac{h-r}{r})+(h-r) \cdot \sqrt {2 \cdot h \cdot r- h^2} ] [/math]

Come vedi, la formula non è immediata. Se il cilindro fosse stato in posto in verticale sarebbe molto più semplice, invece col cilindro posto in orizzontale occorre fare un po' di fatica in più. Ma vediamo la dimostrazione di quanto scritto.

Iniziamo enunciando l'equazione generale di una circonferenza nel piano cartesiano, quando abbia il centro nell'origine:

[math]x^2+y^2=r^2[/math]

Per una questione di comodità di calcolo, però, consideriamo una circonferenza che sia tangente all'asse delle ascisse. In questo modo l'altezza h raggiunta dal liquido corrisponderà proprio al valore y. Possiamo cioè utilizzare il valore dell'ordinata raggiunta dal liquido per indicarne la sua altezza.

L'equazione di una circonferenza tangente all'asse y è:

[math]x^2+(y-r)^2=r^2[/math]

Risolvendo rispetto ad x, otteniamo le due soluzioni dell'equazione di secondo grado:

[math] x_1= - \sqrt{ 2 \cdot r \cdot y - y^2} [/math]

[math] x_2 = +\sqrt { 2 \cdot r \cdot y - y^2} [/math]

Ciascuna delle due è una semicirconferenza. Scegliamo di concentrarci sulla seconda e la moltiplichiamo per due in modo da avere un'intera circonferenza.

Così facendo, otteniamo:

[math] x_2 = +2 \sqrt { 2 \cdot r \cdot y - y^2} [/math]

A questo punto, ci basterà integrare rispetto all'incognita y. Come estremi di integrazione scegliamo proprio 0 ed h, cioè l'altezza iniziale e quella finale del liquido contenuto all'interno della cisterna:

[math] \int_0^h +2 \sqrt { 2 \cdot r \cdot y - y^2} dy [/math]

Svolgendo l'integrale e proseguendo i calcoli otteniamo l'equazione di un segmento circolare corrispondente alla parte piena della cisterna vista in sezione.

[math] \frac{ \pi \cdot r^2}{2}+r^2 \cdot \arcsin (\frac{h-r}{r})+(h-r) \cdot \sqrt {2 \cdot h \cdot r- h^2} [/math]

Per ottenere il volume della parte piena della cisterna, occorre moltiplicare quanto appena ottenuto per L, cioè la lunghezza totale della cisterna.

Per ulteriori approfondimenti sulla circonferenza e il segmento circolare, vedi anche qua.

Per ulteriori approfondimenti sul calcolo del volume mediante l'utilizzo di integrali, vedi anche qua.

Verifica numerica

In questo paragrafo effettueremo alcune verifiche sostituendo alle variabili presenti nella formula alcuni valori ben precisi, in modo da prendere anche dimestichezza con questo tipo di esercizio.

Quando si ha a che fare con una formula lunga o articolata, può essere utile, per comprenderla meglio, vederne il comportamento in alcuni casi peculiari. In questo caso, possiamo inizialmente supporre che il serbatoio sia vuoto, cioè che il livello dell'acqua contenuto in esso, cioè l'altezza h, sia pari a zero.

In questo caso si avrebbe:

[math] L \cdot \frac{ \pi \cdot r^2}{2}+r^2 \cdot \arcsin (\frac{0-r}{r})+(0-r) \cdot \sqrt {2 \cdot 0 \cdot r- 0^2} [/math]

E quindi:

[math] L \cdot \frac{ \pi \cdot r^2}{2}+r^2 \cdot \arcsin (-1)+(0-r) \cdot 0 [/math]

Osservando che:

[math] r^2 \cdot \arcsin (-1)= -r^2 \cdot \arcsin (1) [/math]

e che:

[math] \arcsin (1) = \frac {\pi}{2} [/math]

si ha:

[math] V = \frac{ \pi \cdot r^2}{2} - \frac { \pi \cdot r^2}{2} = 0 [/math]

proprio come ci aspettiamo che sia. Se la cisterna è vuota il volume del liquido è zero.

Come altro caso limite, possiamo considerare quello del serbatoio completamente pieno. In questo caso, quello che ci aspettiamo è che il volume del liquido sia esattamente uguale a quello del cilindro che lo contiene.

Dobbiamo dunque porre

[math]h=2r[/math]
e sostituire questo valore all'interno della formula.

Si ha:

[math] V = L \cdot [ \frac { \pi r^2}{2} + r^2 \cdot \arcsin (1) + r \sqrt {4r^2 - 4r^2} ] [/math]

Osservando che l'ultima radice quadrata è pari a zero perché zero è il valore del radicando, si arriva a:

[math] V = L \cdot \pi r^2 [/math]

che è proprio la misura del volume del cilindro, come ci aspettavamo.

Come calcolare il volume in litri?

In questo tipo di esercizio, la richiesta riguarda il volume occupato da una certa sostanza. In questo paragrafo approfondiamo il concetto di volume e vediamo nel dettaglio le sue unità di misura.

Con la parola volume, intendiamo lo spazio fisicamente occupato da un corpo o da una sostanza. Per misurarlo, si possono utilizzare diverse unità di misura. Nel Sistema Internazionale, esso viene misurato in metri cubi.

Il metro cubo (

[math] m^3 [/math]
) ha i suoi multipli e i suoi sottomultipli, in analogia con quelli del metro. Abbiamo quindi:
  • il kilometro cubo
    [math] km^3 = 1.000.000.000 \, m^3 [/math]
  • l'ettometro cubo
    [math] hm^3 = 1.000.000 \, m^3 [/math]
  • il decametro cubo
    [math] dam^3 = 1.000 \, m^3[/math]
  • il decimetro cubo
    [math] dm^3 = 0,001 \, m^3 [/math]
  • il centimetro cubo
    [math] cm^3 = 0,000001 \, m^3 [/math]
  • il millimetro cubo
    [math] mm^3 = 0,000000001 \, m^3 [/math]

Un'altra unità di misura che viene spesso utilizzata, anche nella vita quotidiana, è il litro, che si indica con la lettera L. Un litro di una qualsiasi sostanza equivale ad un decimetro cubo di quella stessa sostanza. Abbiamo dunque che, per formare un metro cubo, per esempio di acqua, occorrono mille litri d'acqua. Anche il litro, come tutte le unità di misura, ha i suoi multipli e i suoi sottomultipli, come l'ettolitro (hL), il decilitro (dL) o il millilitro (mL).

Altre equivalenze utili sono:

  • [math] 1 \, L = 1000 \, mL [/math]
  • [math]1 \, L = 10^{-3} \, m^3[/math]
  • [math]1 \, mL = 1 \, cm^3[/math]

Per ulteriori approfondimenti sulle unità di misura di volume, vedi anche qua.

Vuoi approfondire Analisi Matematica – Esercizi, problemi e formule di Analisi Matematica con un insegnante esperto?
Trovalo su Ripetizioni.it