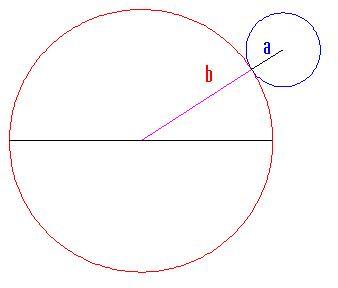
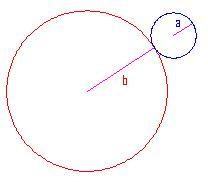
Incominciamo disegnando un piccolo cerchio di raggio all'esterno di uno più grande di raggio
.
Raggi dei cerchi:
Useremo per disegnare il cerchio più grande in forma parametrica ed
per quello più piccolo.
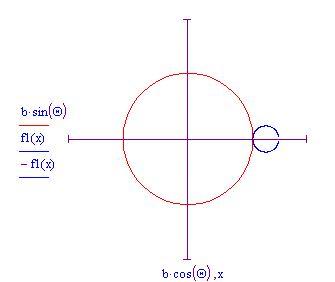
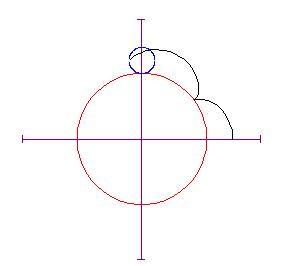
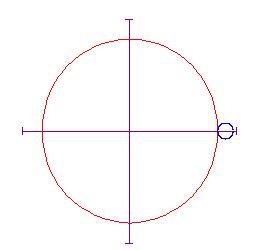
Il cerchio più piccolo inizia a rotolare in senso antiorario lungo la circonferenza del cerchio più grande. Se teniamo il nostro occhio fermo su un punto del cerchio di raggio a , esso traccia una curva man mano che il cerchio rotola partendo dal punto
Metteremo a punto un'animazione che ci mostrerà la curva descritta dal cerchio ruotante. Con un pò di trigonometria ed il disegno qui sotto,
possiamo trovare le equazioni parametriche per la curva tracciata da un punto del cerchio di raggio a ;
dove è l'angolo formato dalla linea che congiunge l'origine con il centro del cerchio esterno e l'asse
. La curva sarà:
Ci piacerebbe animare il disegno della curva facendo variare i valori dell'angolo . Dobbiamo disegnare il cerchio ruotante in qualsiasi posizione
.
In tale posizione il nostro cerchio ha centro:
Usando l'equazione del cerchio
Troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in ogni posizione
Cambiando qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata da esso. (Tutti gli angoli sono misurati in radianti.)
Ripetiamo l'impostazione data usando la variabile k come parametro per far variare l'angolo .
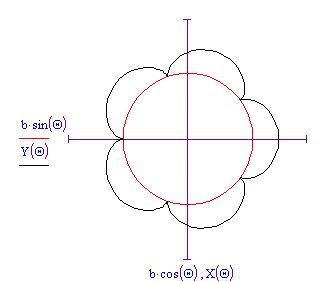
Epicicloide:
curva generata da un punto del cerchio di raggio a che rotola sul cerchio di raggio b
equazioni parametriche dell'epicicloide:
autore Carlo Elce
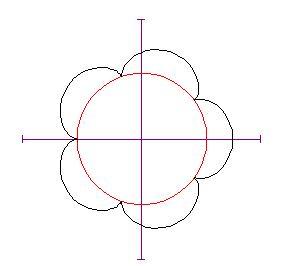
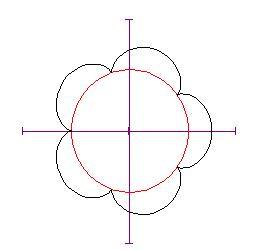
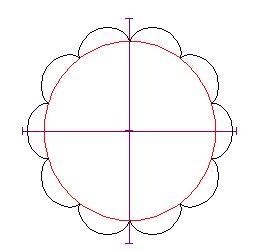
Nota il valore determina il numero di cuspidi presenti nel grafico. Se imposti
ad un valore più grande — diciamo 10 — vedrai un grafico di questo genere:
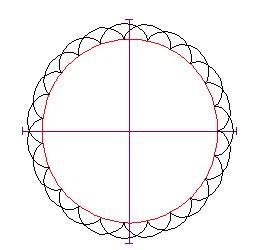
Se il valore di non è un intero, il punto sul cerchio ruotante non tornerà al punto di partenza e se lo fai continuare a girare (poni
maggiore di 2 p ) vedrai un comportamento diverso della curva
non intero
Epicicloide con il rapporto
autore Carlo Elce
Ci si potrebbe divertire cambiando i parametri di questo disegno e animandolo!