_stan
di _stan
(320 punti)
7' di lettura
Il Demiurgo: stabilisce la legge e valuta se le ipotesi proposte sono congrue con essa.
Il Verificazionista: cerca conferme, verifiche delle sue ipotesi.
Il Falsificazionista: cerca di scoprire se le sue ipotesi sono false.

A. Einstein: "Nessuna quantità di esperimenti potrà dimostrare definitivamente che ho ragione; un unico esperimento potrà dimostrare che ho sbagliato".


Albert Einstein ed Enrico Fermi

E. Fermi: "Se il risultato conferma le ipotesi hai appena fatto una misura.

Se il risultato è contrario alle ipotesi, allora hai fatto una scoperta".

Personaggi

Il Demiurgo: stabilisce la legge e valuta se le ipotesi proposte sono congrue con essa,
Il Verificazionista: cerca conferme, verifiche delle sue ipotesi,
Il Falsificazionista: cerca di scoprire se le sue ipotesi sono false.

Il Gioco

Il Demiurgo stabilisce la legge per una serie di numeri. Supponiamo che la legge sia: " Numeri crescenti qualsiasi". Scrive la legge e la deposita sul tavolo in busta chiusa senza mostrarla ai due scienziati (Il Verificazionista e il Falsificazionista). Poi mostra ai due una sequenza di tre numeri compatibili con la legge. Supponiamo che i tre numeri siano: "2,4,6,…". A questo punto propone ai due scienziati di fare delle ipotesi proponendo loro triplette di numeri che dovrebbero essere compatibili con la legge a loro sconosciuta. Per ogni tripletta proposta sarà il Demiurgo, come se fosse il risultato di un esperimento, a dire se la tripletta proposta è congrua o no con la legge.

Il Verificazionista

  1. Propone "8,10,12". Congrua;
  2. Si fa l'idea che la legge sia: "Numeri pari, crescenti per 2";
  3. Per sicurezza propone: "14, 16, 18". Congrua;
  4. Dichiara: "la legge è Numeri pari crescenti per 2". Sbagliato!

Il Falsificazionista

  1. Intuisce che la legge potrebbe essere "Numeri pari crescenti per 2". Prova però a falsificarla;
  2. Propone "8, 10, 14". Congrua. Dunque non è necessario che crescano per due;
  3. Propone "8, 10, 11" Congrua. Dunque non è necessario che siano pari;
  4. Propone "8, 10, 9" Non Congrua;
  5. Propone "8, 10, 10" Non Congrua. Dunque è necessario che i Numeri siano crescenti;
  6. Propone "1, 26, 137" Congrua;
  7. Dichiara: La legge è: "Numeri crescenti qualsiasi". Corretto!
Ecco in 14 pillole la storia della induzione/deduzione e verifica/falsificazione
  1. Già Aristotele distingueva tra deduzione (Generale >>> Particolare) e Induzione (Particolare >>> Generale);
  2. F.Bacone e poi G.Galilei, si basarono sulla osservazione empirica dei fatti, quindi principalmente sulla Induzione;
  3. L'illuminismo francese si concentrò sulle sorti "Magnifiche e Progressive della Ragione e della Scienza";
  4. L'illuminismo scozzese (principalmente D. Hume) fece una critica serrata al concetto di Induzione. Venne poi la metafora di B. Russell relativa al tacchino induttivista;
  5. Lo Statunitense C. Peirce per primo parlo di "falsificazione". Egli inoltre, accanto alla deduzione ed induzione, introdusse l'abduzione: una specie di ingegneria inversa (dai Risultati ai Principi);
  6. Il Positivismo (compreso quello logico di R. Carnap, M. Schlick, O. Neurath,...) stabilì che tutto quello che non era verificabile empiricamente (come ad esempio la metafisica) era privo di senso;
  7. Per Popper la metafisica non è priva di senso, semplicemente è non-scienza. Criterio di demarcazione tra Scienza/Non Scienza è la falsificabilità (e non verifica) degli enunciati;
  8. Per Khun la scienza non progredisce continuamente (come sostenuto da illuministi e Popper), ma per Scienza Normale e Rivoluzioni (cambio di paradigmi);
  9. La posizione di Khun appare estrema. Non ci sono drastici cambiamenti di paradigmi e tanto meno ripartenze da zero. Newton diceva:"mi appoggio su spalle di giganti". Einstein non ha cancellato Newton;
  10. Duhem e Quine criticarono Popper perché non esistono "Experimentum Crucis" e perché gli esperimenti sono sempre "Impregnati di Teoria", dunque non si possono falsificare singole ipotesi scientifiche (Olismo);
  11. Lakatos, allievo di Popper, corroborò le teorie del maestro sulla base della sua idea degli "slittamenti dei programmi di ricerca". Cercò di conciliare Kuhn e Popper;
  12. Fayerabend, allievo di Popper e grande amico di Lakatos, contestò radicalmente il maestro. Negò in "Contro il metodo", l'esistenza di qualunque possibile demarcazione Scienza/non Scienza;
  13. Curiosamente il pensiero di Fayrabend si salda con gli ermeneutici, decostruzionisti/pensiero debole (Gadamer, Derrida, Vattimo, ecc.): "Non esistono fatti ma solo interpretazioni";
  14. Tra i filosofi oppositori del pensiero debole/decostruzionisti/ermeneutici ci sono i "nuovi realisti" tra cui l'italiano Maurizio Ferraris, già allievo di Vattimo e Derrida, che sostengono l'utilità di concetti come "verità" e "oggettività".

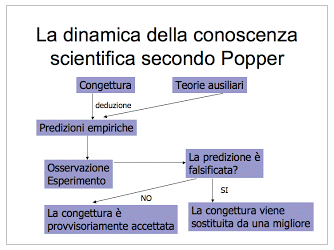
La dinamica della conoscenza scientifica secondo Popper

Il problema teorico che si pone Popper è come cresce la conoscenza. La sua soluzione è uno schema tetradico molto semplificato del metodo di eliminazione per prove ed errori.

P1 >> TP >> EE >> P2

P1 denota il problema dal quale partiamo, può trattarsi sia di un problema pratico che teorico;
TP è una teoria provvisoria che si propone per risolvere il problema;
EE denota un processo di eliminazione degli errori, attraverso controlli e processi di discussione critica,
P2 denota infine i problemi coi quali concludiamo, emersi dalle discussioni e dai controlli.

L'intero schema mostra che si parte da problemi (pratici o teorici) si tenta di risolverli creando una teoria provvisoria. Si sottopone poi la teoria al controllo tentando di falsificarla: è questo il metodo critico di eliminazione degli errori. Dal processo emergeranno uno o più problemi risultanti chiamati P2.
La crescita della conoscenza, cioè del progresso compiuto può essere stimato sulla base della differenza tra P2 e P1. In breve lo schema dice che la conoscenza parte da problemi e si conclude con problemi (se mai si conclude).
Per Popper tutta la nostra conoscenza rimane fallibile e congetturale. Il vecchio ideale scientifico della conoscenza assolutamente certa, dimostrabile si è rivelato un idolo. L'esigenza dell'oggettività scientifica rende ineluttabile che ogni asserzione della scienza rimanga necessariamente e per sempre allo stato di tentativo. Non al possesso della conoscenza, della verità irrefutabile, mira l'uomo di scienza, ma alla ricerca critica, persistente ed inquieta della verità.

"Il nostro compito di scienziati non è di scegliere solo i fatti che confermano una teoria e - per così dire - la ripetono; il metodo scientifico consiste invece nella ricerca di fatti che possano confutare una data teoria." Karl Raimund Popper.

Riferimenti

Vuoi approfondire Logica con un insegnante esperto?
Trovalo su Ripetizioni.it