Affidabilità

Agraria

L'affidabilità (reliability) di un sistema, un'apparecchiatura, un circuito, misura la sua probabilità di funzionare correttamente per un tempo predeterminato (tempo di missione).
Naturalmente qualunque sistema dal più semplice, una lampadina, al p

…continua

Anteprima

Vedrai una selezione di 1 pagina su 3

Disdici quando
vuoi

Acquista con carta
o PayPal

Scarica i documenti
tutte le volte che vuoi

Sintesi

L'affidabilità (reliability) di un sistema, un'apparecchiatura, un circuito, misura la sua probabilità di funzionare correttamente per un tempo predeterminato (tempo di missione).
Naturalmente qualunque sistema dal più semplice, una lampadina, al più complesso, un satellite, è composto da più parti che tutte debbono contribuire per il funzionamento complessivo dell'intero sistema.

Nella progettazione ingegneristica il concetto di affidabilità utilizza le due principali concezioni matematiche di probabilità disponibili: quella soggettiva (De Finetti, Ramsey) per progetti innovativi e quella frequentista (Von Mises) per progetti standard a lungo consolidati e monitorati.

Esaminiamo ora le leggi basilari che regolano l'interazione tra il funzionamento di un sistema e delle sue componenti, indicando con (P) l'affidabilità, cioè la probabilità che la parte del sistema funzioni per tutto il tempo di missione, e quindi con (1 - P) la probabilità che il sottosistema si guasti prima del compimento del tempo di missione.

Parti in serie

Qualunque sistema complesso può essere schematizzato da un insieme di componenti diverse collegate in serie che tutte debbano funzionare per far funzionare l'intero sistema nel suo complesso. Nella figura rappresentata sotto si vedono due sottosistemi collegati in serie e la relativa affidabilità.

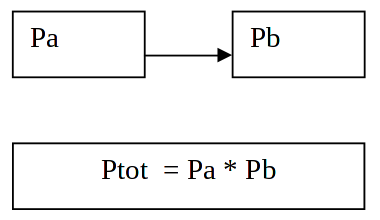
Dunque la affidabilità di due sottosistemi collegati in serie è sempre inferiore all'affidabilità del minore dei due ed è calcolabile come prodotto dell'affidabilità di "a" per quella di "b". E' immediata la estensione ad n elementi collegati in serie:

[math] Ptot = \Pi (Pi) (i=1, ..., n) [/math]

Parti in parallelo

Si potrebbe pensare che per sottosistemi in parallelo la legge sia che le probabilità si sommano, così non è, anche perché aggiungendo componenti, si supererebbe presto la soglia Ptot > 1 incompatibile con il concetto stesso di probabilità (Ptot <= 1).
Per calcolare la affidabilità di due sottosistemi collegati in parallelo è necessario innanzi tutto calcolare le singole probabilità di guasto: (1 - Pa) e (1 -Pb). Poi la probabilità di guasto totale: (1 - Pa) * (1 - Pb). Il sistema si guasta quando si guastano entrambe le parti, dunque la probabilità di guasto dell'intero sistema è sempre inferiore alla probabilità di guasto delle singole parti.

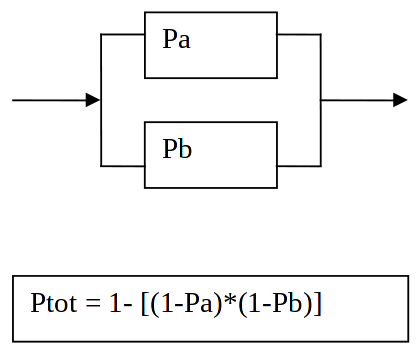
Solo a questo punto è possibile calcolare (vedi la formula riportata sopra) l'affidabilità di due sottosistemi collegati in parallelo. Dalla formula si evince che la affidabilità di due sottosistemi collegati in parallelo è sempre superiore all'affidabilità dei singoli sottosistemi. E' immediata la estensione ad n elementi collegati in parallelo:

[math] Ptot = 1 - \Pi (1 - Pi) (i=1, ..., n) [/math]

Parti in serie, ma con ridondanza dei sottosistemi

Si considerino ancora due sottosistemi collegati in serie (a e b). Per aumentare l'affidabilità del sistema nel suo complesso, a ciascuno dei due sistemi è stato posto in parallelo un sottosistema identico ad "a" e "b" rispettivamente. Dunque la probabilità di guasto di "a" sarà:

[math](1 - Pa)^2[/math]

e quella di "b":

[math](1 - Pb)^2[/math]

. Quindi l'affidabilità di "a" sarà:

[math][1 - (1 - Pa)^2][/math]

e quella di "b"

[math][1 - (1 - Pb)^2][/math]

. Sotto è riportata l'affidabilità dell'intero sistema: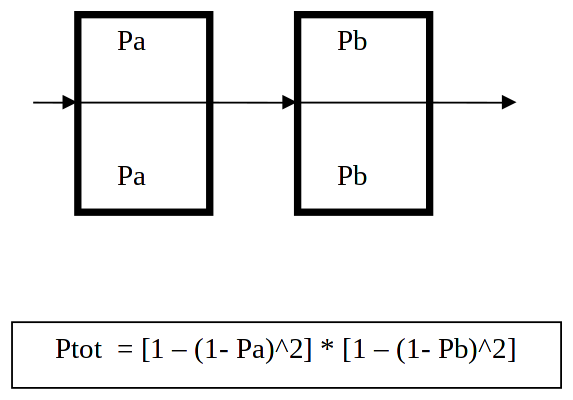

Questa formula può essere generalizzata al caso in cui si abbiano n sistemi in serie composti da sottosistemi che abbiano ciascuno probabilità di guasto Pi e ni parti in parallelo:

[math] Ptot = \Pi [1 – (1 – Pi)^{ni}]\,\,\,\,\,\,\,\,\,\, (i = 1, \ldots, n) [/math]

Un esempio numerico

Consideriamo il caso della progettazione di un sistema innovativo formato da 5 unità che devono funzionare, tutte e contemporaneamente, per garantire il funzionamento dell'intero apparecchio per il tempo ritenuto necessario (tempo di missione).
Per ciascuna unità siano pure note le seguenti specifiche:

Affidabilità per il tempo di missione (%)
Costo (Migliaia di Eur.)
Peso (Kilo grammi)
Volume (Metri cubit)

Nome Unità	A	B	C	D	E
Affidabilità	60%	85%	80%	90%	95%
Costo (K.Eur)	10	30	8	50	20
Peso (Kg.)	1	3	0.5	2	2
Volume (Mc.)	0.1	0.5	0.2	0.3	0.4

Numero Unità (Ni)	1	1	1	1	1

Con questi dati numerici, abbiamo la seguente situazione in termini di Affidabilità., Probabilità di guasto, Costo, Peso e Volume dell'intera apparecchiatura:

Affidabilità	34.9%
Prob Guasto	65.1%

Valori Totali
Costi (K. Eur)	118
Pesi (Kg.)	8.5
Volumi (Mc.)	1.5
Tot. Unità	5

La affidabilità del sistema è piuttosto bassa e per contro la probabilità di guasto troppo alta. Questi livelli sono sicuramente non accettabili nella industria aereo spaziale, nucleare, difesa, sicurezza informatica/bancaria e in molti altri settori. Vediamo nel seguito come migliorarla.

Kettelle

John Kettelle (1925 - 2012) era un matematico americano impegnato nei sottomarini durante la guerra di Corea degli anni 50.
Si impegnò a lungo nello studiare matematicamente, utilizzando il calcolo delle probabilità e le tecniche di ottimizzazione, come migliorare la affidabilità dei sistemi sfruttando la ridondanza (parti in parallelo o in stand-bay), ma rispettando i vincoli di progetto sui limiti di, costi, pesi, volumi, ecc. L'algoritmo da lui trovato per questo specifico problema procede per stadi successivi ed è assimilabile alla programmazione dinamica. Vediamo i risultati ottenuti con un vecchio software (kettelle) applicato al nostro problema.

Massimizzare l'affidabilità del sistema (inserendo unità in parallelo)

Con vincoli:

Costo, inferiore agli 800.000 Eur
Peso, inferiore ai 40 Kilogrammi
Volume, inferiore a 5 Metri cubi
Totale Unità, non più di 30.

Nome Unità	A	B	C	D	E
Affidabilità	60%	85%	80%	90%	95%
Costo (K.Eur)	10	30	8	50	20
Peso (Kg.)	1	3	0.5	2	2
Volume (Mc.)	0.1	0.5	0.2	0.3	0.4

Numero Unità (Ni)	5	3	4	3	3

F. Obiet. (Affidab.)	0.9837335
Prob Guasto	0.0162665

Vincoli:
Costi (K. Eur.)	382	<=	800
Pesi (Kg.)	28	<=	40
Volumi (Mc.)	4.9	<=	5
Tot. Unità	18	<=	30

Dunque, aggiungendo 2 unità in parallelo a B,D,E; 3 unità in parallelo a C; e 4 unità ad A si ottiene un sensibile miglioramento della affidabilità del sistema (dal 35% a oltre il 98%) rispettando tutti i vincoli imposti su Costi, Pesi e Volumi.
Si può subito osservare che la soluzione trovata non è ottimale (non sappiamo se la colpa sia dell'algoritmo di Kettelle o, più probabilmente, del vecchio software utilizzato).
Il vincolo più vicino alla saturazione è quello sui Volumi (5 Mc.) che con la soluzione proposta impiega (4.9 Mc.). E' dunque possibile aggiungere una unità in parallelo al componente A (0.1 Mc.) migliorando l'affidabilità del sistema complessivo (da circa il 98% a circa 99%). Ecco la nuova soluzione:

Nome Unità	A	B	C	D	E
Numero Unità (Ni)	6	3	4	3	3

F. Obiet. (Affidab.)	0.9898401
Prob Guasto	0.0101599

Vincoli:
Costi (K. Eur.)	392	<=	800
Pesi (Kg.)	29	<=	40
Volumi (Mc.)	5	<=	5
Tot. Unità	19	<=	30

Soluzione Ottimale

Vediamo ora come il nostro esempio numerico iniziale può essere tradotto in un modello matematico di ottimizzazione che massimizzi la affidabilità globale del sistema inserendo "ni" unità in parallelo, ma rispettando tutti i vincoli del problema:

Funzione Obiettivo, Affidabilità (F):

[math]F = {[1-(1-0.6)^n1] \cdot [1-(1-0.85)^n2] \cdot [1-(1-0.8)^n3] \cdot [1-(1-0.9)^n4] \cdot [1-(1-0.95)^n5]}[/math]

[math]Max! (F)[/math]

Vincoli:

10*n1 + 30*n2 + 8*n3 + 50*n4 + 20*n5 <= 800 KEur Costi
n1 + 3*n2 + 0.5*n3 + 2*n4 + 2*n5 <= 40 Kg. Pesi
.1*n1 + .5*n2 + .2*n3 + .3*n4 + .5*n5 <= 5 Mc. Volumi
n1 + n2 + n3 + n4 + n5 <= 30 Num. Unità

Variabili intere:

n1, n2, n3, n4, n5

Si tratta di un problema di programmazione matematica con vincoli lineari, funzione obiettivo non lineare e variabili intere. Quindi abbastanza complesso. Vediamo quali sono i risultati forniti dal Risolutore di Excel:

Nome Unità	A	B	C	D	E
Numero Unità (Ni)	7	3	4	4	2

F. Obiet. (Affidab.)	0.990818
Prob Guasto	0.009182

Vincoli:
Costi (K. Eur.)	432	<=	800
Pesi (Kg.)	30	<=	40
Volumi (Mc.)	5	<=	5
Tot. Unità	20	<=	30

Dunque la soluzione ottima del problema porta la affidabilità dell'intero sistema ad un valore superiore al 99%, inserendo 20 unità in parallelo con un costo di 432.000 Eur e impiegando interamente i 5 Metri cubi di spazio disponibili.

Conclusioni

Nel paragrafo precedente abbiamo assunto come funzione obiettivo da Massimizzare l'affidabilità globale del sistema. Potevamo in alternativa stabilire la affidabilità desiderata come un vincolo imprescindibile e come funzione obiettivo la minimizzazione dei costi (o dei volumi o dei pesi, ecc.). Si deve rammentare che la programmazione matematica può essere vista come un sistema a due livelli: obiettivo primario è la soddisfazione di tutti i vincoli, poi, nell'ambito della regine ammissibile, si ottimizza la funzione obiettivo.
In una ottica Goal Programming si potrebbe anche pensare di dare un peso a ciascun obiettivo (Affidabilità, Costi, Peso, Volumi, ecc.) per poi ottimizzare il tutto, ma l'argomento esula dagli scopi di questo breve articolo. Chi volesse approfondire il problema o avere altri esempi concreti di programmazione matematica può, tra l'altro, guardare/riferirsi al lavoro di Hume e Smith citato in bibliografia.