_stan
di _stan
(320 punti)
18' di lettura
Le metodologie dello studio di reti e grafi possono trovare un notevole numero di applicazioni pratiche: progettazione di una rete stadale, ferroviaria, aerea, navale, intermodale, ecc.

Si potrebbe inoltre trattare di eliminare, modificare o aggiungere un tronco su una rete già esistente ecc. La rete inoltre potrebbe essere elettrica, idraulica, di telecomunicazioni, teleriscaldamento, metanodotti, oleodotti, ecc. Nel piccolo poi queste tecniche possono essere utilizzate per progettare il lay-out di uno stabilimento manifatturiero o addirittura le connessione ottimali di un circuito integrato.

Più in generale va osservato che i valori dei vari tronchi (Archi) della rete potrebbero essere sostituiti da grandezze diverse dai km, ad esempio: costo, resistenza, reddito, probabilità, ecc.
Sarebbe ad esempio possibile cercare il sistema meno oneroso con il quale degli oggetti passino, con riferimento al caso riportato sotto, da un sistema iniziale 1) ad un sistema finale 12); naturalmente alle lunghezze dei vari archi andrebbe sostituito il costo di transizione da uno stato all'altro.

La teoria dei Grafi fu ideata da Eulero e la leggenda racconta che lui la inventasse per risolvere il problema dei ponti di Koenisberg che avevano i suoi concittadini per programmare la loro passeggiata domenicale.

Eulero trovò che in un qualunque grafo si può trovare un cammino chiuso che attraversi gli archi una sola volta, se l'ordine di tutti i nodi del grafo è pari, mentre si può trovare un cammino euleriano aperto se vi sono solo due nodi (che saranno quello di arrivo e quello di partenza) di ordine dispari. Si può facilmente verificare che, sia nel caso dei ponti di Koenisberg che di quello del grafo riportato sotto non esiste soluzione. Cioè, in entrambi i casi, non è possibile progettare un percorso (chiuso o aperto) che tocchi una e una sola volta tutti gli archi del grafo.

Noi abbiamo a disposizione i fogli elettronici che Eulero non aveva e che sino alla fine degli anni 70 dello scorso secolo non esistevano. Possiamo dunque facilmente tracciare, come fatto sotto, il Grafo iniziale del nostro problema riportando i valori (Chilometri o costi o altro) su ogni arco del grafo; questo ci permette e facilità sia la visualizzazione della rete che le possibilità di calcolo. Per calcolare il costo totale della rete sarà sufficiente utilizzare la funzione =Somma(da:a) estendendola dalla cella sopra il grafo a sinistra a quella sotto il grafo a destra.
Un piccolo intoppo viene dal fatto che in questa maniera la somma conteggia anche la numerazione dei nodi del grafo. Ricordate cosa rispose il piccolo Gauss al maestro che gli chiedeva di conteggiare la somma dei primi n numeri naturali? (

[math]n\cdot(n+1)/2[/math]
). Ebbene nel nostro caso sara sufficiente sottrarre al totale:
[math]12*13/2 = 78[/math]
.

GRAFO INIZIALE

Grafo iniziale

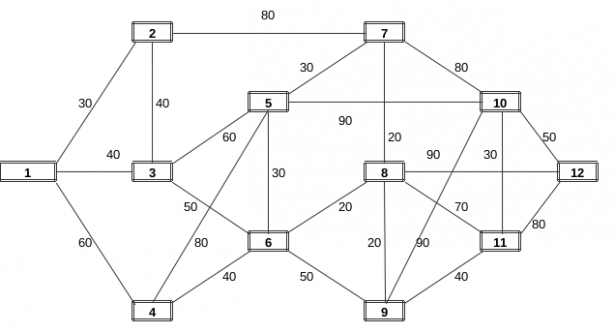
Totale Num. Archi: 24

Totale Costo Archi: 1270

Connessione Ottima

Si consideri ora il seguente problema. Dato il grafo iniziale che connette 12 città (i costi di connessione sono riportati sugli archi), si vuole cercare come stendere la rete in fibra ottica in modo tale che tutte le città abbiano tra loro un cammino di connessione al costo minimo. In termini di teoria dei grafi il problema si traduce nella ricerca di: "un sottografo che sia albero completo avente costo minimo". Vediamo il significato dei termini: Sottografo significa una parte del grafo originario, Albero significa un grafo che non ha circuiti chiusi, Completo significa che deve toccare tutte le 12 città.

Kruscal ha trovato un algoritmo straordinariamente semplice per risolvere in modo ottimale questo problema, esso appartiene alla famiglia degli algoritmi "Greedy" o Ingordi. Gli algoritmi "Ingordi" si gettano subito sugli aspetti più convenienti (nel caso gli archi a costo più basso) per rivolgere poi la loro attenzione a quelli via via più cari. Il fatto è che in genere gli algoritmi ingordi possono ortare al massimo ad una buona soluzione, raramente a quella ottima (soprattutto se il problema è di dimensioni considerevoli). Ebbene Kruscal ha mostrato che nella ricerca di un albero completo di costo minimo relativo ad un grafo, l'algoritmo Greedy consente sempre di trovare la soluzione ottimale.

Si comincia selezionando i tre archi da 20 (non ha importanza l'ordine con cui vengono presi).
Si procede scegliendo i tre archi da 30. Si noti che esiste un quarto arco da 30 tra i nodi 5 e 7, ma esso non può essere selezionato perché si genererebbe il circuito 5-6-8-7-5. Abbiamo poi tre nodi da 40 (il quarto è escluso perché chiuderebbe il circuito 1-2-3-1). Infine scegliamo 2 nodi da 50. Il procedimento si arresta perché l'albero ricopre tutti i nodi del grafo. Grazie a Kruskal abbiamo la certezza che la rete in fibra ottica così progettata sia quella di costo minimo (Totale 370).

ALBERO di COSTO MINIMO (algoritmo di KRUSCAL)

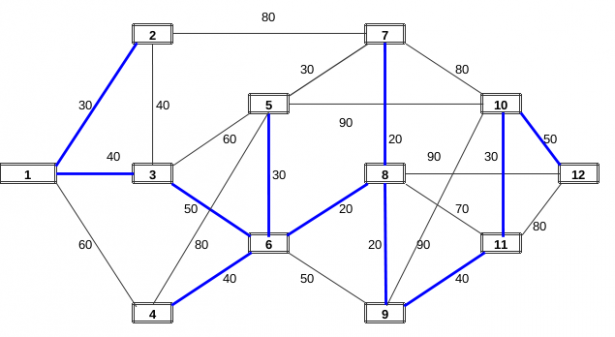
Totale Albero Completo a Costo Minimo
3 archi da 20 60
3 archi da 30 90
3 archi da 40 120
2 archi da 50 100
Totale 370

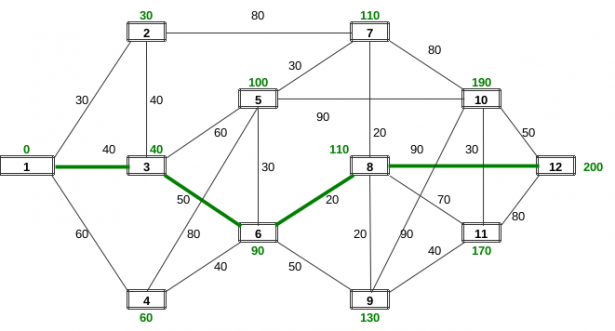
Cammino Ottimo

Consideriamo ora il problema di dover raggiungere, partendo dalla città 1, la città 12 seguendo il percorso a chilometraggio più breve (Problema del Cammino più breve attraverso una rete/grafo). Disponendo sull'auto di un navigatore il problema è facilmente risolto. Vi siete però mai chiesti a quale algoritmo si affidino i navigatori satellitari? Si tratta dell'algoritmo di Dijkstra che risolve il problema in tempi Polinomiali al crescere del numero dei vertici e degli archi del grafo. Va precisato che gli algoritmi Polinomiali (P) sono facilmente trattabili e risolubili dai computer, mentre i problemi Non Polinomiali (NP), cioè quelli per cui non è conosciuto un algoritmo polinomiale, sono difficili anche per i computer più veloci. Vediamo come procede Dijkstra partendo dal nodo 1. Il nodo 2 può essere raggiunto solo da una arco di lunghezza 30, dunque etichettiamo con 30 il nodo 2. Con ragionamento analogo etichetteremo con 60 il nodo 4. Per decidere come etichettare il nodo 3 dobbiamo confrontare due cammini: quello diretto 1-3 di Km 40 e quello indiretto 1-2-3 di Km 70. Scegliamo il minimo ed etichettiamo con 40 il nodo 3. Si procede in questa maniera, per etichettare ciascun nodo, il cammino più breve che ad esso porta. Facilmente l'algoritmo risolve il problema: il cammino più breve da 1 a 12 transita per i nodi 1-3-6-8-12 con un totale di 200 Chilometri.

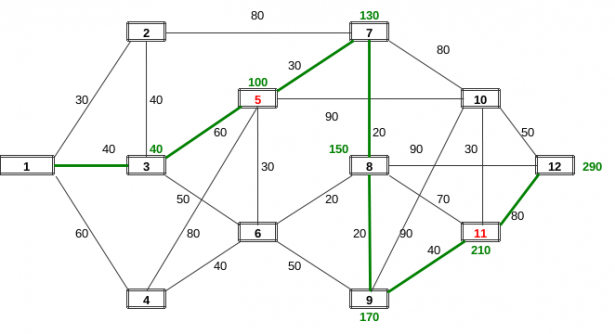
Supponiamo che ora, giunti alla città 3 il programma del gruppo di amici sull'auto cambi, essi infatti decidono di voler visitare anche le città 5 e 11. Da 3 a 5 il percorso minimo è già definito dalla ricerca
precedente (100 Km.). Dobbiamo poi applicare l'algoritmo di Dijkstra tra il nodo di partenza 5 e il nodo di arrivo 11 che implica, dalla partenza, 210 chilometri. Infine l'arrivo alla città 12 dopo aver percorso 290 Km.

Per concludere si osservi che questo problema, della ricerca del cammino minimo su un grafo, è del tutto analogo al problema della ricerca del cammino delle attività a durata massima di un progetto (attività critiche) che illustreremo più avanti.

CAMMINI di COSTO MINIMO (algoritmo di DIJKSTRA)

CAMMINO DI COSTO MINIMO, dovendo includere i centri 5 e 11

Circuito Ottimo

Cercare un cammino Hamiltoniano su un grafo significa cercare, partendo da un nodo, un circuito che tocchi tutti i nodi del grafo una sola volta tornando alla fine al nodo di partenza.
Il problema del "Commesso viaggiatore" consiste nella ricerca, su un grafo, di un cammino Hamiltoniano di costo minimo. Per la soluzione di questo problema non sono conosciuti a tutt'oggi algoritmi che lo risolvano in tempi Polinomiali, ciò sigifica che se il numero dei vertici e degli archi del grafo è elevato non esiste un computer che, per quanto veloce e potente, possa risolvere il problema in modo ottimale con tempi di calcolo ragionevoli. Negli ultimi anni si è andata sviluppando una tecnica di simulazione (vedi su Wikipedia "Simulated Annealing" e "Travelling salesman problem") che consente di trovare, anche per grandi grafi, soluzioni soddisfacenti e spesso ottime.

Vediamo ora come un semplice problema può essere affrontato con una tecnica euristica di tipo "Greedy", la stessa che ha permesso di trovare la soluzione ottimale alla costruzione dell'albero a costo minimo con l'algoritmo di Kruskal (Per avere una prima stima del costo minimo di un circuito Hamiltoniano alcuni suggeriscono di moltiplicare per 2 il valore ottimo trovato per l'albero a costo minimo. Nel nostro esempio

[math]370*2 = 740[/math]
).

Si consideri il caso di una città portuale (nodo 1) che riceve periodicamente via navi, merci da distribuire via Tir alle altre11 città della regione. Si tenga presente che i Tir debbono toccare tutte le città una sola volta tornando al porto del nodo 1 scarichi. Per tentativi ed errori cerchiamo di ipotizzare il circuito Hamiltoniano in modo tale da scegliere gli archi meno costosi (o meno lunghi). Al primo tentativo si trova il circuito: 1>2>3>5>7>10>12>11>8>9>6>4>1:costo 610. Osserviamo ora che il percorso 11>8>9>6 può essere modificato nel percorso 11>9>8>6 risparmiando 30+30 = 60. Dunque il nuovo circuito Hamiltoniano a costo presumibilmente minimo è: 1>2>3>5>7>10>12>11>9>8>6>4>1 che ha un costo totale di 550. Naturalmente non si ha la certezza che questo sia l'ottimo assoluto. Si lascia al lettore la verifica dell'esistenza di altri cammini Hamiltoniani migliori.

PROBLEMA DEL COMMESSO VIAGGIATORE (tecniche EURISTICHE)

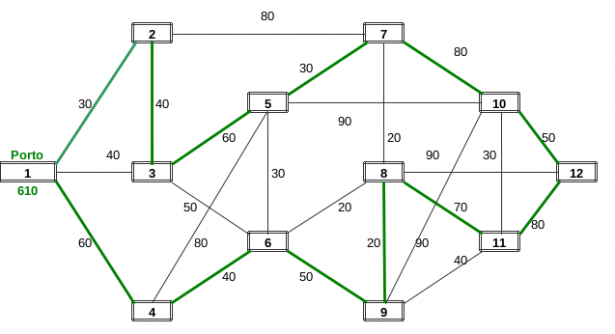
Totale circuito Hamiltoniano 1 trovato
1 > 2 30
2 > 3 40
3 > 5 60
5 > 7 30
7 > 10 80
10 > 12 50
12 > 11 80
11 > 8 70
8 > 9 20
9 > 6 50
6 > 4 40
4 > 1 60
Totale 610

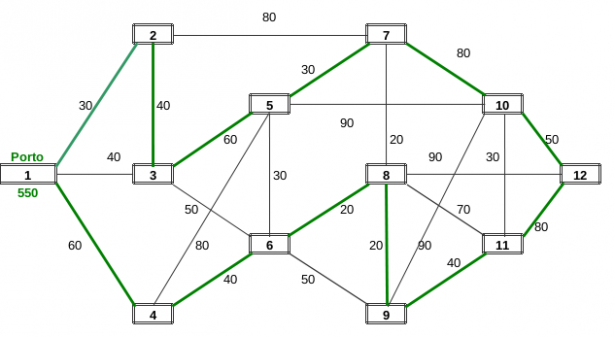
Totale circuito Hamiltoniano 2 trovato
1 > 2 30
2 > 3 40
3 > 5 60
5 > 7 30
7 > 10 80
10 > 12 50
12 > 11 80
11 > 9 40
9 > 8 20
8 > 6 20
6 > 4 40
4 > 1 60
Totale 550

Durata di un progetto

Sino ad ora abbiamo considerato lo spazio (misurato in Km o in Costi per percorrerli) come il sottostante di un grafo, altra possibilità è considerare il tempo misurato in giorni. Si pensi ad un progetto composto da 24 attività rappresentate dai 24 archi del grafo (si parla di rappresentazione AOA "Activities On Arrows" che è in alternativa ad AON "Activty On Nodes"). I nodi del grafo rappresentano gli istanti di inizio e fine di ciascuna attività e sull'arco è riportato il numero di giorni necessario a completare l'attività. Ci si chiede in quanto tempo potrà essere completato l'intero progetto partendo dall'evento 1 (giorno 0), istante di inizio. L'evento 2 (fine dell'attività 1-2) avverrà dopo 30gg, mentre l'evento 4 (fine dell'attività 1-4) avverrà dopo 40gg.

Per calcolare l'evento 3 dobbiamo confrontare la durata dell'attività 1-3 (30gg) con quella del percorso 1-2-3, cioè: 40 con 30 + 40 = 70 e scegliere il massimo cioè 70. Analogamente il tempo dell'evento 5 sarà dato da: Max[(60+70),(80+60))] = 140° giorno. Procedendo in modo analogo sino al nodo 12 possiamo concludere che il progetto sarà completato in 1 anno e 55 giorni. In rosso sono indicate le attività critiche, cioè le attività che, se ritardate, manderanno in ritardo l'intero progetto. Le altre attività hanno un margine di scorrimento che può essere facilmente calcolato effettuando un percorso all'indietro partendo dal nodo 12, 420° giorno e sottraendo man mano le durate delle singole attività. Chi volesse avere la descrizione dell'intero processo: "Forward Pass, Early Dates, Backword pass, Late Dates, Late-Early = Total Float" può trovarlo sul libro: "Tecniche di Project Management". Il libro illustra anche la tecnica "Precedence" che adotta la notazione AON e consente una più flessibile gestione dei vincoli oltre il consueto vincolo "Finish to Start" tra le attività che nell'esempio abbiamo adottato.

Naturalmente oggi nessuno calcola a mano i reticoli CPM, esistono softwares (ad esempio Winproject della Microsoft) che lo fanno in modo eccellente trasformando i risultati in diagrammi di Gantt, la visualizzazione preferita dai gestori di progetto. Tuttavia conoscere gli algoritmi di calcolo permette di comprendere e valorizzare al meglio i risultati dei computer.

TECNICHE RETICOLARI (PERT-CPM)

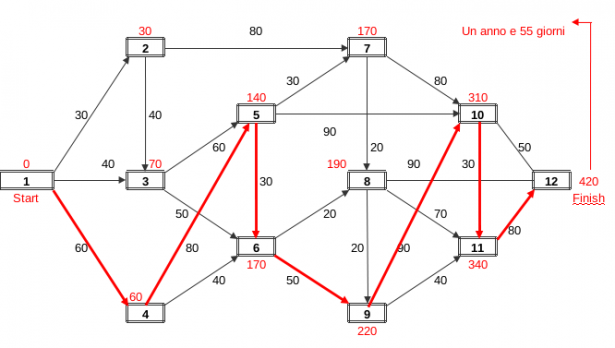
Flusso Massimo su Rete

Torniamo ora alla dimensione spaziale del nostro grafo interpretandola però come una rete autostradale che connette una regiane dove su ciascun arco del grafo è riportata la capacità massima dell'arteria espressa in numero dei veicoli/ora. Si debba ricercare il massimo flusso orario dei veicoli, consentito dalla rete fra il 1° e il 12° centro.

Per prima cosa si può osservare che il flusso massimo attraverso la rete sarà necessariamente inferiore od uguale alla capacità massima uscente dal nodo 1 iniziale: dunque 2,200. Inoltre possiamo facilmente evincere che il flusso massimo attraverso la rete sarà inferiore od uguale alla capacità massima entrante nel nodo 12 finale: dunque 2,150. Siamo quindi certi che attraverso la rete non potranno fluire più di 2,150 veicoli l'ora. Esiste un teorema, "Max Flow = min Cut", anche molto intuitivo, il quale garantisce che il flusso massimo che può attraversare la rete coincide con il taglio, a capacità minima, della rete stessa in due tronconi. Nella nostra rete relativamente piccola (12 città e 24 tronchi autostradali) possiamo facilmente trovare, con qualche tentativo, che il flusso massimo sopportabile tra 1-12 è pari a 1850 veicoli all'ora. Se la rete è grande e se vogliamo conoscere nel dettaglio il flusso su ciscun tronco autostradale, si può ricorrere al metodo del Simplesso di Dantzig. Esiste inoltre un algoritmo polinomiale (Il Simplesso non lo è) specifico per questo problema sviluppato da Ford e Fulkerson.

FLUSSO MASSIMO DI RETE

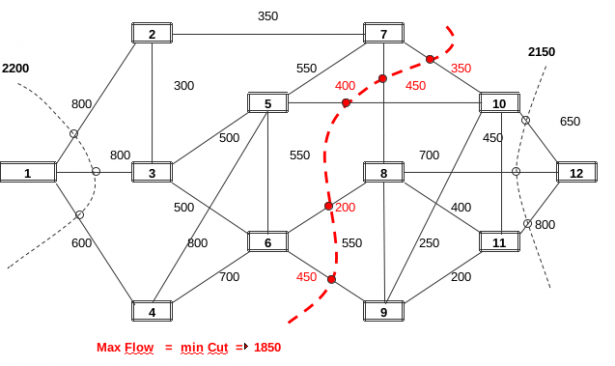
Conclusioni

Nello scorso secolo la teoria delle reti ha continuato ad evolversi aggiungendo sempre nuovi capitoli: reti biologiche, reti sociali, reti informative (in particolare Internet), ecc. Inoltre nella scienza si è andato diffondendo un nuovo paradigma che contrappone alla tradizionale visione riduzionista della scienza, che ha portato ai grandi successi della fisica, della biologia molecolare ecc, una visione olistica e complessa in cui tutto è connesso come in una rete. Quanto questo nuovo paradigma sia efficacie è ancora da verificare.

Paul Erdos, introdusse le reti casuali che hanno cioè dei nodi con un numero medio -massimo di link e due code verso destra e sinistra che si estinguono rapidamente. Cioè reti ben descritte dalla distribuzione normale di Gauss. Ad esempio questo tipo di reti descrive efficaciemente la rete stradale e autostradale degli Stati Uniti. Esistono però reti diverse, come quella che connette i principali aereoporti Statunitensi dove sono fondamentali gli Hub come New York, Los Angeles, Huston, Detroit, ecc. In queste reti (chiamate anche a invarianza di scala) Il numero dei Link dei nodi sono meglio descritti da una legge di potenza piuttosto che da una legge normale. Le leggi casuali di potenza prevedono pochi nodi con tanti link (gli hub) e tanti nodi con pochi link.

Chi volesse approfondire questi temi può riferirsi al libro citato di Barabasi. Ricordando che come sosteneva K. R. Popper "la ricerca non ha fine" e, in accordo con K. Lorenz: "il futuro è aperto".

Riferimenti

Vuoi approfondire Applicazioni con un insegnante esperto?
Trovalo su Ripetizioni.it