_stan
di _stan
(320 punti)
35' di lettura
Un algoritmo può essere definito come una sequenza ordinata e finita di istruzioni elementari che conduce in un tempo finito a un determinato risultato. Vediamo degli esempi semplici.

Indice

Introduzione

La voce "Algoritmo" di Wikipedia riporta una definizione generale, completa e sintetica del termine.
Un algoritmo è:

"Una sequenza ordinata e finita di passi (operazioni o istruzioni) elementari che conduce a un ben determinato risultato in un tempo finito".

Vediamo un semplice esempio di algoritmo per risolvere il problema di appendere un quadro:

  1. cercare un chiodo adatto,
  2. cercare un martello,
  3. mettere il chiodo nella posizione desiderata sul muro,
  4. martellare,
  5. se il chiodo non è ben fissato tornare al punto 4,
  6. se il chiodo è ben fissato andare al punto 7,
  7. appendere il quadro,
  8. Fine.
Anche la ricetta di cucina per fare la pasta alla Carbonara può essere tradotta in un algoritmo. Gli algoritmi possono essere usati per risolvere problemi esecutivi, decisionali, previsionali, ecc. Le aree maggiori d'impiego sono nell'informatica, smartphone, robotica e intelligenza artificiale. Se gli algoritmi hanno a che fare con la matematica, si parla di algoritmi numerici. Un bell'elenco di algoritmi numerici e dei loro inventori è stato fatto da Trefethen dell'università di Oxford (vedi Riferimenti).

In questo articolo ci occuperemo principalmente di un particolare tipo di algoritmi numerici chiamati "Avidi" o "Ingordi" (in inglese Greedy). Si chiamano avidi perché ad ogni iterazione si gettano sul valore più alto (se il problema è di Massimo) o su quello più basso (se il problema è di Minimo). Si tratta di Algoritmi che portano a soluzioni buone, molto buone e talora ottime. Faremo poi un confronto con l'algoritmo del Simplesso che trova sempre soluzioni ottime per i problemi di Programmazione lineare. Lo schema che seguiremo nella presentazione dei vari casi è il seguente:

Problemi >>> Algoritmi >>> Codici >>> Soluzioni.

Consideriamo, per iniziare, il problema di un comune montano, formato da 4 frazioni (A,B,C,D), che debbono essere collegate con la fibra ottica. I costi preventivati per i collegamenti tra le frazioni, considerando anche gli attraversamenti del fiume e della strada provinciale, sono:

A-B 10
A-C 30
A-D 50
B-C 20
B-D 30
D-C 40
Il problema può essere rappresentato dal grafo riportato sotto in cui sui nodi si rappresentano le frazioni del comune e sugli archi i costi di allacciamento.

Naturalmente non è necessario attivare tutti i collegamenti degli archi del grafo (Costo totale = 10 + 30 + 50 + 20 + 35 + 40 = 185). E' sufficiente costruire un collegamento tra le 4 frazioni che le tocchi tutte, non preveda duplicazioni di percorso (cicli) e costi il meno possibile. In altri termini si tratta di costruire sul grafo un albero completo di costo minimo.
Come costruire questo albero lo ha suggerito Kruskal con il suo algoritmo (vedi Riferimenti) Greedy che è anche ottimale: cioè il ricoprimento di un grafo con un albero completo, secondo l'algoritmo di Kruscal, porta sempre ad una soluzione di costo minimo. Vediamo come si può descrivere, in forma di pseudo codice, l'algoritmo:

  1. Scegliere il primo arco di costo minimo,
  2. Scegliere il secondo arco di costo minimo,
  3. Individuare il successivo arco di costo minimo,
  4. Se chiude circuiti scartare l'arco, tornare al punto 3,
  5. Se non chiude circuiti scegliere l'arco ed escluderlo da ulteriori considerazioni,
  6. Se tutti i nodi non sono stati toccati tornare al punto 3,
  7. Se tutti i nodi sono stati toccati andare al punto 8,
  8. Fine.
Vediamo ora come l'algoritmo si applica al nostro esempio del comune montano con le 4 frazioni:

Si seleziona l'arco A-B, costo 10,
Si seleziona l'arco B-C, costo 20,
Si dovrebbe selezionare l'arco A-C, costo 30, ma esso chiuderebbe il circuito ABC. E' scartato,
Si selezione l'arco B-D costo 35,
Tutte le frazioni (ABCD) sono toccate e l'algoritmo si arresta.

Costo totale della fibra ottica = 10 + 20 + 35 = 65. che è anche il costo minimo ottenibile. In questo tipo di problemi su grafo l'algoritmo Greedy porta sempre alla soluzione ottima.

Il Problema del trasporto

Il primo a occuparsi di programmazione lineare fu il russo Kantorovich che, partendo dal metodo dei moltiplicatori di Lagrange, lavorò per la pianificazione sovietica al problema della allocazione delle risorse, senza però avere i dovuti riconoscimenti dai burocrati del regime. Nel 1939 Kantorovich ideò il metodo dei potenziali per risolvere i problemi di trasporto (che sono un caso particolare di problema di programmazione lineare). Nel 1947 Dantzig, partendo dai lavori di Leontieff e Kantorovich ideò, per il problema generale di Programmazione Lineare, il metodo del Simplesso, forse l'algoritmo di maggior successo nella storia della matematica. Nel 1975 Kantorovich e Koopmans vinsero il premio Nobel per l'economia, l'esclusione di Dantzig da quel premio creò non poche polemiche. Oggi, a 70 anni dalla sua invenzione, l'algoritmo del Simplesso resta (benché siano stati inventati algoritmi con complessità polinomiale come "il metodo dei punti interni" di Karmarkar) tra quelli codificati nei software di maggior successo/diffusione, valgano per tutti le tabelle elettroniche.
Vediamo nel seguito, con un esempio numerico, in cosa consistono i problemi di trasporto e come possono essere affrontati con il metodo Greedy della "Matrice minima".
Relativamente ad uno specifico prodotto abbiamo tre produttori che dai loro magazzini (M1, M2, M3) possono offrire sul mercato rispettivamente 50, 40 e 60 unità di prodotto. Abbiamo poi, situati in aree geografiche diverse, tre clienti (C1, C2, C3) che richiedono rispettivamente: 20, 95 e 35 unità di prodotto. In totale si ha: Offerta = Domanda = 150 unità di prodotto. Nelle singole celle della matrice sono riportati i costi unitari di trasporto dal magazzino Mi al cliente Cj (5,8,4; 6,6,3; 3,9,6).
L'algoritmo della "Matrice Minima" è piuttosto semplice:
  1. Nella matrice dei Costi si sceglie la cella a valor Minimo,
  2. Si trasporta dal Magazzino al Cliente il Massimo consentito dai vincoli di Domanda/Offerta,
  3. Se è saturata l'offerta del Magazzino, si cancella la rispettiva riga dei Costi,
  4. Se è saturata la richiesta del Cliente, si cancella la rispettiva colonna dei Costi,
  5. Se tutte le Domande e le Offerte sono saturate, si salta al punto 7,
  6. Se tutte le Domande/Offerte non sono saturate, si torna al punto 1,
  7. Si calcola la funzione Obiettivo: Unità trasportate * Costi unitari di trasporto (In Excel =Matrice Somma.Prodotto),
  8. Fine.
In pratica invece di cancellare le Righe/Colonne è più semplice assegnare ad esse un valore molto elevato, in tal modo sarà lo stesso algoritmo (che cerca i costi Minimi) a scartare quelle celle. Nel nostro esempio numerico dopo aver selezionato la cella M3-C1 (3) ed avere allocato nello STEP.1 il massimo consentito dalla domanda del cliente C1 (20), invece di cancellare la Colonna C1 nella matrice dei costi si è assegnato ad essa il valore 999. In questa maniera sarà lo stesso algoritmo ad ignorare C1 in quanto i suoi costi sono troppo elevati.

Questo semplice esempio numerico (matrice 3x3) è stato risolto in 5 passi dall'algoritmo Greedy
Il costo globale dei trasporti (Funzione Obiettivo), ottenuto moltiplicando le quantità trasportate indicate nello STEP.5 con i costi unitari riportati nello STEP.0 da un valore di 955. Questo valore non è ottimale, ma molto buono e vicino all'ottimo. Infatti l'algoritmo ottimale del Simplesso, fornisce un minimo di 920. Dunque l'algoritmo Greedy , in questo caso, supera (nel senso che è peggiore) l'ottimo solo per il (955 - 920)/920 = 3.8%. Tuttavia vogliamo rilevare che nel campo dei trasporti, notoriamente molto competitivo, una variazione di costo del 3.8% non è certo trascurabile. Del resto si consideri, per esemplificare, il caso di un'azienda che abbia: Ricavi = 100, Costi = 95, Profitti = 5. Una riduzione dei costi del 3.8% porta a: Ricavi =100, Costi = 91.39, Profitti = 8.61 cioè un aumento di 3.61 che in termini percentuali significa un aumento del 72% del Profitto al lordo delle imposte.
L'algoritmo del Simplesso (Poliedro Convesso) si chiama così perché nei problemi di programmazione matematica che hanno tutti i vincoli lineari, la regione ammissibile, cioè la regione ad n dimensioni (n = numero delle variabili, nel nostro esempio 9) che rispetta tutti i vincoli, assume la forma di un poliedro convesso. Dantzig ha mostrato due risultati fondamentali che sono alla base dell'algoritmo:

  1. La soluzione ottimale si trova sempre su un vertice del Simplesso (o in rari casi su uno spigolo/faccia),
  2. L'algoritmo è in grado di evolvere da un vertice all'altro, migliorando sempre la funzione obiettivo, sino al raggiungimento della soluzione ottimale.

Vediamo ora qual è la soluzione ottimale trovata dall'algoritmo del Simplesso per il nostro problema:

Perché l'algoritmo Greedy non è riuscito a trovare l'ottimo? Perché avidamente, nei primi due Step, si è gettato sui trasporti a più basso Costo (3) scegliendo le celle M3-C1 e M2-C3, precludendosi così la possibilità di trovare la soluzione globalmente più economica.

Problema di Trasporto 20x10 (Simplesso)

Consideriamo ora un problema analogo al precedente, ma di dimensioni più grandi e quindi più realistico.
Una società produttiva ha stoccato un tipo di merce nei suoi 20 magazzini in una determinata area commerciale.
Nella medesima area deve rifornire con la merce 10 clienti sparsi nel territorio.
Si assume che la quantità totale di merce immagazzinata coincida con la domanda totale dei clienti.
Ogni cliente può essere rifornito in tutto o in parte da qualsiasi magazzino.
E' disponibile per ogni coppia magazzino-cliente il costo di trasporto della merce.
Si vuole determinare l'intera distribuzione magazzini-clienti che renda minimo il costo di trasporto totale. Il numero di variabili (quantità che dai magazzini/righe vanno ai clienti/colonne) sono 20 x 10 = 200.

Vediamo ora come il problema può essere formalizzato da un punto di vista matematico.

Sia:

Mi Magazzini (i = 1…20)
Cj Clienti (j = 1…10)
Oi Offerta di ciascun Magazzino (i = 1…20)
Dj Domanda di ciascun Cliente (j = 1…10)

cij costo unitario di trasporto dal Magazzino Mi al Cliente Cj (i = 1…20, j = 1…10)
Xij Variabili: Quantità trasportate dal Magazzino i al Cliente j (i = 1…20, j = 1…10).

VINCOLI

(\sum Xij) per ogni magazzino = Oi (j = 1…20). Ogni magazzino può offrire solo quanto detiene
( \sum Xij) per ogni cliente = Cj (i = 1…10), Ogni cliente può ricevere solo quanto richiede.

FUNZIONE OBIETTIVO

Min ( \sum\sum Xij * cij ) (i = 1…20, j = 1…10). Costo totale che deve essere minimizzato

E' interessante osservare come con il risolutore EXCEL (vedi il file TRASPORTO MERCI allegato) sia semplice impostare un problema di questo tipo/dimensioni solo con quattro istruzioni:

  1. Minimizzare la cella dei Costi Totali di trasporto (impostando la cella obiettivo)
  2. Indicare, usando il range; le celle che contengono le 200 variabili (cambiando le celle)
  3. Garantire che tutti i Clienti abbiano le quantità desiderate (Vincoli domanda)
  4. Garantire che tutti i Produttori/Magazzini eroghino solo quanto disponibile (Vincoli offerta).
Soluzione Ottimale dei trasporti trovata dal Simplesso con il Risolutore Excel:


Linee di Bus

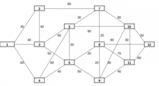
Vediamo ora un problema di trasporto urbano.
In una cittadina, a seguito delle elezioni comunali viene eletta una nuova amministrazione. Il sindaco, anche per dimostrare di essere una persona attiva e decisa, convoca il presidente della società comunale dei trasporti e gli chiede di migliorare sostanzialmente il servizio, per dar seguito alle promesse elettorali della nuova giunta. Dopo qualche settimana viene dunque elaborato un nuovo piano dei trasporti pubblici, realizzata da autobus. Nuovi percorsi ed una diversa pianificazione delle fermate. Il piano prevede cinque linee di bus per coprire le aree urbane, come da disegno sotto riportato.

Sono disponibili n= 60 bus che dovranno essere distribuiti tra le diverse linee per assicurare il servizio nell'arco di 18 ore al giorno. Da statistiche e stime tecniche si è determinato il numero minimo di passeggeri che occorre trasportare per ogni linea. Si ricerca la distribuzione di bus (quanti bus per ogni linea) per massimizzare il numero totale dei passeggeri giornalieri.
Il problema è così schematizzato:

[math]n_i[/math]
= numero bus linea i
[math]n = 60[/math]
= numero totale bus
[math]N_i[/math]
= numero corse giornaliere linea i
[math]p_i[/math]
= numero passeggeri trasportati sulla linea i al giorno
[math]p_(i,min)[/math]
= numero passeggeri minimo da trasportare sulla linea i al giorno
(\tau) = numero ore servizio bus giornaliero = 18
(\tau_i) = durata ciclo linea i (per durata si intende il tempo totale di percorrenza A/R)
[math]c[/math]
= capienza bus = 40 persone

[ N_i = frac{\tau}{\tau_i} n_i]

[ p_i = cN_i ]

Funzione obiettivo da massimizzare:

[ F = mbox{Max}\sum_i p_i = c\tau ast mbox{Max} \sum_i frac{n_i}{\tau_i} ]

dove le variabili sono le

[math]n_i[/math]

Vincoli:

[ n_i quad mbox{interi} ]

[ \sum_i n_i le n ]

[ p_i ge p_{i,min} ]

Il problema è di tipo lineare a numeri interi e si risolve facilmente con il Simplesso, ma anche con il metodo GRG non lineare ed il metodo Evolutivo.

La soluzione ottima è la seguente:

con un trasporto di 24400 persone/giorno.
I dettagli sono riportati nel file EXCEL LINEE BUS.

Progetti - Contrattisti

Supponiamo che nel mondo, per il prossimo anno siano previste gare per 25 nuovi Progetti (Raffinerie, Impianti Chimici, Centrali elettriche, Condotte, Porti, Piattaforme marine, Strutture sottomarine, ecc.)
(P1…P25), questi progetti possono essere On-Shore e Off-Shore e Grandi (G) o Medio Piccoli (MP). I Contrattisti internazionali che possono realizzarli sono 8 (C1...C8).
C1 può fare solo progetti di mare, ma di qualunque dimensione (G). C2 può fare solo progetti di terra e di dimensione medio piccola. C3 e C4 possono realizzare sia progetti di mare che di terra, ma di dimensione medio piccola. C5...C8 possono realizzare qualunque tipo di progetti (G). Si deve tenere conto del carico di lavoro già in essere: nell'ultima riga (Max New Proj) sono indicati il numero massimo di nuovi progetti che possono essere acquisiti da ciascun contrattista. Non sono previste joint venture (2 contrattisti che collaborano allo stesso progetto)
Nella matrice P-C è riportato un indicatore multicriteri (compreso tra 0 e 100) che tiene conto di quanto un contrattista è adatto (Area geografica, Cliente, Navi e attrezzature, Fattori politico economici, Reputazione, Lobbies) a realizzare uno specifico progetto. L'indicatore assume valore 0 se il contrattista non può eseguire lo specifico progetto. L'indicatore assume il valore 100 se si sa già che quel progetto verrà acquisito dallo specifico contrattista.. Nell'esempio, 5 progetti sono già stati assegnati.

Indice Multicriteri

La pianificazione strategica di uno dei Contrattisti deve cercare di prevedere come saranno ripartiti tra gli 8 General Contractor i 25 lavori previsti per il prossimo anno. Per stabilirlo si utilizza un metodo simile a quello indicato da De Finetti per valutare le Probabilità Soggettive. In Pratica si utilizzano le conoscenze degli esperti di marketing sui progetti, i contrattisti e sulla loro propensione a lavorare insieme. L'ufficio studi ha identificato sei parametri, cui a dato un peso, per valutare la bontà degli accoppiamenti. Vediamo com'è costruito questo indice Multicriteri, facendo riferimento, ad esempio, al valore calcolato per l'abbinamento tra il Progetto P1 e il Contrattista C1.

Analogo lavoro deve essere fatto per gli 8x25 = 200 possibili abbinamenti tra i progetti e i contrattisti. I risultati sono riassunti nella matrice riportata nel prossimo paragrafo.

Matrice Progetti-Contrattisti

Nel caso dei trasporti il problema era: minimizzare i Costi di Trasporto rispettando i vincoli in questo caso dobbiamo massimizzare il punteggio totale nel rispetto dei vincoli. In questa maniera troveremo quella assegnazione dei progetti ai contrattisti che, secondo il parere degli esperti, ha la massima probabilità di avverarsi. Affrontiamo inizialmente il problema con un algoritmo Greedy a stadi successivi:
  1. Si assegna il primo progetto (P1) al contrattista che ha punteggio massimo,
  2. Si diminuisce di 1 la capacità del contrattista cui il progetto è assegnato,
  3. Si escludono da ulteriori considerazioni i contrattisti che non hanno più capacità,
  4. Si assegna il progetto successivo al contrattista, con capacità, che ha punteggio massimo,
  5. Si diminuisce di 1 la capacità del contrattista cui il progetto è assegnato,
  6. Se tutti i progetti sono assegnati, saltare al punto 9
  7. Se tutti i contrattisti hanno esaurito la propria capacità, saltare al punto 9
  8. Se ci sono ancora progetti da assegnare tornare al punto 3
  9. Fine
Nella matrice riportata sotto nella colonna Max Proj sono ricopiati i punteggi con cui vengono assegnati i progetti:

E' evidente che questo algoritmo Greedy a stadi è in generale piuttosto inefficiente in quanto dipende dall'ordine (nell'esempio siamo partiti da P1 per arrivare a P27) con cui vengono selezionati i progetti. Potremmo ad esempio partire dal fondo o dal centro, ecc. Gli algoritmi a stadi successivi (come la programmazione dinamica) danno risultati ottimali solo per alcune classi di problemi o per alcuni valori dei dati. Nell'esempio numerico riportato sopra i vincoli sulle capacità dei contrattisti non sono operanti (è come se non esistessero) pertanto scegliere, ordinandoli da P1 a P27, per ciascun progetto, il contrattista a punteggio massimo garantisce la soluzione ottima: punteggio totale 2237. Dunque in questo caso specifico abbiamo:

Greedy a stadi = Matrice massima = Simplesso = 2237

Mentre in generale per questo tipo di problema, che è di Massimo, si ha:

Greedy a stadi

Vediamo ora quali sono i passi dell'algoritmo Matrice (Mij) Massima applicato a questo tipo di problemi:

  1. Si cerca il valore massimo della intera matrice Mij >>> Si memorizza il valore Vmax, Progetto (Pi), Contrattista (Cj),
  2. Si cancella, o si azzera, l'intera riga del progetto (Pi) nella matrice Mij,
  3. Si riduce di 1 la capacità Vj del contrattista che si è assegnato il progetto,
  4. Quando la capacità Vj di un contrattista viene azzerata si cancella o si azzera, nella matrice Mij, la colonna del Contrattista (Cj),
  5. Si torna al punto 1 sino a quando tutti i progetti sono assegnati o le capacità dei contrattisti esaurite. Altrimenti si va al punto 6,
  6. Fine
Nella matrice riportata sopra è trascritto nell'ultima colonna (Ordine MatMax) l'ordine con cui vengono fatte le assegnazioni secondo questo algoritmo. Possiamo osservare che:
  1. Prima vengono assegnati i progetti acquisiti (con punteggio 100), dal 1° al 5°
  2. Poi vengono assegnati i progetti con punteggio 99: 6° e 7°
  3. Poi viene assegnato il progetto con punteggio 98, lo 8°
  4. Poi viene assegnato il progetto con punteggio 95, ecc.
Infine, per illustrare come non sia banale il passaggio da un algoritmo a un codice implementabile sul computer, abbiamo riportato in appendice il codice Visual Basic utilizzabile in Excel, che traduce l' algoritmo della matrice massima sopra descritto.

Diversamente dagli algoritmi euristici, cui appartengono i metodi Greedy, i modelli di Ottimizzazione, basati sulla Programmazione Matematica, richiedono una formalizzazione precisa. Vediamo come procedere, utilizzando come esempio il problema Progetti-Contrattisti.

Sia:

Pi Progetti (i = 1…25)
Cj Contrattisti (j = 1…8)
VJ Max New Projects, per Contrattista

Mij Indice Multicriteri (i = 1…25, j = 1…8)
Xij Variabili bivalenti, zero-uno (i = 1…25, j = 1…8). Le Xij assumono valore 1 se il Progetto i è assegnato al Contrattista j. Altrimenti assumono valore zero

VINCOLI

(\sum Xij) per ogni progetto ( \sum Xij le Vj) per ogni contrattista (i = 1…25), non più di Vj progetti.

FUNZIONE OBIETTIVO

(mbox{Max}\sum\sum Xij ast Mij) (i = 1…25, j = 1…8). Punteggio totale che deve essere massimizzato

Per risolvere questo problema in Excel è necessario costruire accanto alla Matrice Mij , che riporta l'indice di bontà di un accoppiamento tra Progetti e Contrattisti, una matrice Xij (con valore incognito che può assumere il valore zero o uno) che allochi i progetti ai contrattisti rispettando i vincoli del problema:

Un progetto può essere fatto solo da un contrattista. ( Un contrattista non può fare più progetti di quelli consentiti dal suo carico di lavoro ( Sarà dunque necessario calcolare:
In una colonna Somma (Xij) per riga, che dovrà essere In una riga Somma (Xij) per colonna, che dovrà essere La funzione obiettivo, sarà un massimo, ed è data dalla somma dei prodotti delle celle della matrice Mij per Xij.
Si usa la funzione Matr.Somma.Prodotto(intervalloMij; intervalloXij).

L'applicazione del Risolutore con il metodo del Simplesso al nostro problema Progetti-Contrattisti
produce lo stesso risultato ottenuto con il metodo Greedy che, in questo caso, è stato capace di trovare la soluzione ottima. I risultati sono riportati nel file EXCEL PROGETTI-CONTRATTISTI.

Problemi di Assegnazione

Nei problemi di assegnazione, come abbiamo visto anche sopra, i vincoli sono sempre del tipo:

1) (\sum Xij ltgt = K )

mentre in generale un vincolo di programmazione lineare è del tipo:

2) (\sum aij ast Xij ltgt = K )

Cioè nella matrice dei coefficienti dei vincoli di tipo 1) il valore di aij è unitario, nei vincoli di tipo 2) così non è. La matrice dei coefficienti nei vincoli di tipo 1) si dice unimodulare.
Più precisamente una matrice m*n si dice unimodulare quando qualunque sottodeterminante della matrice ha valore: 1,0,-1.
Perché questa distinzione teorica è importante?
La distinzione è importante perché, se le matrici dei vincoli sono unimodulari, si può dimostrare che la soluzione con la programmazione lineare è anche, automaticamente, una soluzione intera. Questa conclusione è di grande utilità pratica in quanto gli algoritmi di PL (Programmazione Lineare) continua (esempio Simplesso) sono molto più efficienti, se applicabili, degli algoritmi a numeri interi (Branch and Bound o metodi evolutivi).
Per Completezza si deve ricordare che per i Problemi di Assegnazione con matrice quadrata (un lavoratore per ciascun lavoro) esiste un algoritmo - denominato Ungherese - molto efficiente che, diversamente dai metodi Greedy, porta sempre alla soluzione ottima. Purtroppo nel nostro caso non può essere utilizzato in quanto la matrice Progetti - Contrattisti non è quadrata e i vincoli non hanno termini noti unitari sia sulle righe che sulle colonne.

Risolutore Excel

Il Solver Excel offre tre algoritmi/metodi per risolvere i problemi di programmazione matematica / ottimizzazione. In realtà gli algoritmi sono cinque e talora possono essere impiegati in modo combinato tra loro. Vediamone un elenco sintetico:
  1. Simplex: utilizzabile quando tutti i vincoli e la funzione obiettivo sono lineari. Per questi problemi l'algoritmo è particolarmente efficiente e veloce. Porta sempre alla soluzione ottimale (salvo rari casi di degenerazione).
  2. Generalized Reduced Gradient (GRG): utilizzabile per problemi non lineari in cui la funzione obiettivo e i vincoli siano derivabili. Se il problema non è convesso può portare solo ad un ottimo locale.
  3. Algoritmi Genetici (EVO): utilizza una generazione casuale di soluzioni, seleziona le migliori e le incrocia tra loro. E' utilizzabile anche per problemi non lineari, non convessi e non lisci (nonsmooth). In generale è molto più lento di Simplesso e di GRG. Ha un suo modo di gestire le variabili intere indipendente da B&B.
  4. Branch&Bound (B&B): Ramifica e Taglia. Si usa con variabili intere o binarie (zero-uno). Viene attivato automaticamente, se necessario, assieme a Simplex o GRG. I Problemi interi o misti sono molto più complessi e lenti da risolvere dei corrispondenti problemi continui.
  5. Alldifferent Constraints: Si usa per problemi a numeri interi di Permutazione, Ordinamento, Sequenza, Commesso viaggiatore. Ad esempio, X1:X5 = alldifferent significa che alle cinque variabili possono essere assegnati tutte e solo le permutazioni dei numeri interi 1…5. Si usa in coppia con Simplex, GRG o EVO.
Dunque per problemi lineari (PL) è raccomandabile il Simplesso anche se GRG ed EVO possono essere utilizzati. Per problemi non lineari convessi (PNL) e raccomandabile il metodo GRG anche se EVO può essere utilizzato. Per i problemi non convessi e non lisci (NSP) è raccomandabile il metodo EVO, anche se si può utilizzare un'accoppiata: EVO nella fase iniziale e GRG nella fase finale per accelerare la convergenza. Per problemi di programmazione lineare a numeri interi (PLNI) è raccomandabile l'accoppiata Simplesso + B& B, attivata del resto automaticamente; oppure il metodo EVO che ha un suo sistema per trattare le variabili intere senza far uso di B&B. Per Problemi di programmazione non lineare a numeri interi (PNLNI) si può usare GRG + B&B oppure EVO. Infine per problemi di Permutazione ordinamento e sequenza si devono utilizzare i vincoli Alldifferent che possono essere accoppiati con Simplesso, GRG ed EVO.
Nella tabella riportata sotto, si cerca di riassumere l'Algoritmo migliore per ciascun Problema (X), ma anche gli altri algoritmi che possono essere utilmente utilizzati (x).

Appendice

Esempio di Codice, che traduce in Visual Basic l'algoritmo della matrice massima applicato al problema dell'assegnazione dei progetti ai contrattisti.
' Ricerca matrice massima con il metodo Greedy

 ' Autore: Hume - 2017

Sub main()

 Dim matd(), val(), vmax As Single

 Dim np, npd, nso, ip, iip, iso, nprso, nmaxso(), iallp(), ndiso(), nallso() As Integer

 For ir = 3 To 31

 For ic = 15 To 23

 Cells(ir, ic) = ""

 Next ic

 Next ir

 ' letture dati

 np = Cells(1, 1).Value ' numero progetti

 nso = Cells(1, 2).Value ' numero partecipanti alle gare

 ReDim matd(np, nso), iallp(np), val(np), nmaxso(nso), ndiso(nso), nallso(nso) ' ridimensionamento matrici

 For ip = 1 To np

 For iso = 1 To nso

 matd(ip, iso) = Cells(4 + ip, 2 + iso).Value ' punteggi assegnati ad ogni contrattista per ogni gara

 Next iso

 Next ip

 For iso = 1 To nso

 nmaxso(iso) = Cells(30, 2 + iso).Value

 ndiso(iso) = nmaxso(iso) ' numero iniziale di progetti ancora disponibili ad ogni contrattista

 Next iso

 npd = np ' numero progetti ancora da esaminare

 ' ----------------------------------------------------------------------------------

 ' Ricerca progetto di valore max e relativo contrattista

 ' con il vincolo che il contrattista abbia ancora progetti disponibili

 100 vmax = 0

 For ip = 1 To np

 For iso = 1 To nso

 If matd(ip, iso) > vmax Then

 iallp(ip) = iso ' contrattista che ottiene il progetto ip

 vmax = matd(ip, iso)

 val(ip) = vmax

 ipmax = ip

 ismax = iso

 End If

 Next iso

 Next ip

 ' verifica che il contrattista abbia ancora progetti disponibili

 If ndiso(ismax) > 0 Then

 ndiso(ismax) = ndiso(ismax) - 1 ' si toglie un progetto al contrattista

 ' cancellare la riga del progetto

 For iso = 1 To nso

 matd(ipmax, iso) = 0

 Next iso

 npd = npd - 1

 If npd > 0 Then GoTo 100

 If npd = 0 Then GoTo 200

 End If

 For iip = 1 To np

 matd(iip, ismax) = 0

 Next iip

 GoTo 100

 200 For iso = 1 To nso

 nallso(iso) = nmaxso(iso) - ndiso(iso)

 Next iso

 ' -----------------------------------------------------------------------------------

 ' stampe

 valtot = 0

 For ip = 1 To np

 iso = iallp(ip)

 Cells(4 + ip, 14 + iso) = val(ip) ' matrice progetti assgnati vs società

 valtot = valtot + val(ip)

 Next ip

 For iso = 1 To nso

 Cells(30, 14 + iso) = nmaxso(iso) ' stampa numero max progetti che ogni società è in grado di gestire

 Cells(31, 14 + iso) = nallso(iso) ' stampa numero progetti allocati ad ogni società

 Next iso

 Cells(29, 23) = valtot

 End Sub

Riferimenti

Vuoi approfondire Applicazioni con un insegnante esperto?
Trovalo su Ripetizioni.it