vuoi
o PayPal
tutte le volte che vuoi
Una particolare situazione si ha quando il bene considerato è una quantità monetaria. Si possono immaginare due casi: nel primo si considera uno stock monetario (la ricchezza o patrimonio), nel secondo si considera un flusso (guadagno o perdita di denaro).
Il primo che storicamente si interessò del problema fu Daniel Bernoulli, che nel 1738 scrisse un saggio sull'argomento (R1). Egli assunse come base della sua teoria la ricchezza, che indichiamo con W (che sta per wealth), ed immaginò che l'utilità fosse funzione della ricchezza:
Secondo Bernoulli l'utilità marginale (derivata dell'utilità
Lo stesso concetto può essere espresso dicendo che la variazione di utilità è proporzionale alla variazione percentuale di ricchezza
Questa semplice equazione differenziale a variabili separabili si integra ottenendo:
La funzione, che tutti gli studenti ben conoscono, è tradotta dal seguente diagramma:
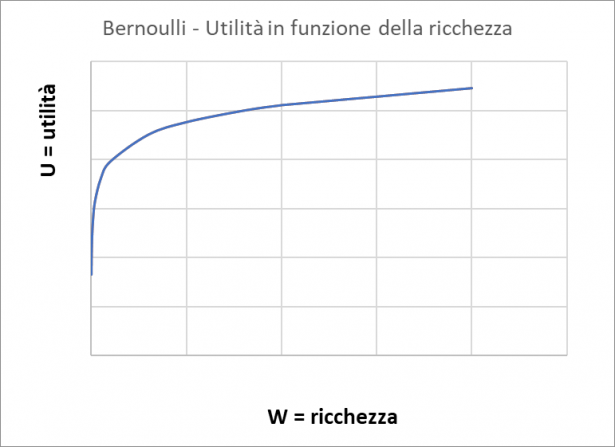
Essa esprime la sua idea che l'utilità non è costante ma dipende dal livello di ricchezza.
Questo è molto convincente dal punto di vista realistico: regalare 1000€ a chi possiede una ricchezza
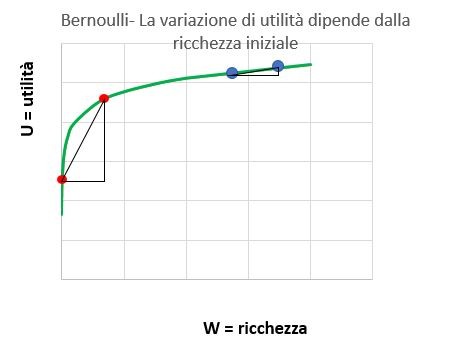
Fin qui siamo sul terreno della certezza. Tuttavia nella vita reale guadagni e perdite abitualmente non sono certi, ma affetti da rischio. Consideriamo ad esempio un investimento industriale: si può immaginare di ottenere un guadagno e la relativa utilità con una determinata probabilità
Se l'esito di una scelta soggetta a rischio (investimento, lotteria, scommessa,..) presenta diversi possibili risultati, ciascuno con una sua probabilità, l'utilità attesa è la somma pesata:
Dove le rispettive
L'economia classica assume che il comportamento dell'individuo, di fronte a scelte che comportano rischio (vale a dire probabilità note o comunque immaginate) calcoli l'utilità media attesa con la
Ad esempio consideriamo un individuo che possiede la ricchezza iniziale
Si può immaginare di calcolare il nuovo livello di ricchezza
Intanto determiniamo la ricchezza per i due possibili esiti:
E quindi calcoliamo l'utilità attesa, iniziale e finale con la
La variazione di utilità risulta:
In questo modo scompare la costante
Per applicare questa teoria ai casi pratici ci serve la costante
In epoca successiva gli economisti hanno rielaborato l'idea nell'ambito della teoria della decisione tralasciando il concetto di utilità e limitandosi, per maggiore concretezza pratica, a valutare guadagni e perdite attese in condizioni di rischio. In breve, la teoria economica classica si limita a calcolare:
Dove
Se sono possibili diverse scelte alternative, ognuna delle quali presenta un insieme di possibili guadagni con le relative probabilità, la teoria economica richiede che per ogni alternativa si calcoli il guadagno atteso con la
Questa teoria normativa è stata lungamente sostenuta dagli economisti fin quando qualcuno ha cominciato a metterla in dubbio nella seconda metà del '900. Si è osservato che il comportamento effettivo dell'individuo di fronte alle scelte economiche è alquanto diverso. Di fatto si è rilevato che la persona è solitamente avversa al rischio. Se deve scegliere tra un guadagno certo ed uno rischioso, l'individuo di solito preferisce l'alternativa certa, a patto che le utilità attese siano comparabili.
Un'osservazione banale: la teoria normativa
Diversi studiosi hanno scelto approcci diversi dalla teoria classica. In particolare, due psicologi Tversky e Kahnemann (in seguito TK) hanno deciso di ritornare all'utilità e dopo lunghe riflessioni sull'argomento hanno sviluppato una teoria quantitativa comportamentale dell'utilità, denominata Prospect Theory (R3).
A differenza della teoria di Bernoulli, basata sulla ricchezza
Tversky e Kahnemann hanno inventato dei test di quella che è stata definita economia sperimentale/ comportamentale di KT e li hanno provati tra di loro. In un secondo tempo hanno ampliato i test, li hanno proposti a gruppi di studenti ed hanno valutato le loro risposte di fronte a diverse alternative che comportano guadagni o perdite soggetti a rischio.
I risultati dei test sono stati elaborati in un modello che, dal punto di vista matematico, possiamo immaginare sia stato costruito nel seguente modo.
Assumiamo, per ora, di trascurare il rischio, riservandoci di introdurlo in uno step successivo.
Si fa l'ipotesi che la variazione % dell'utilità sia proporzionale alla variazione% del guadagno:
Che si integra, ottenendo:
Possiamo esprimere la costante in forma logaritmica:
Quindi:
Ed infine:
(dove
In conclusione KT ottengono una semplice funzione di potenza. I dati sperimentali fittano un valore
La correlazione
In caso di perdite (
Dunque la teoria di TK prevede che l'utilità abbia un ramo positivo rappresentato dalla (3) ed un ramo negativo individuato dalla
Ora ci ricordiamo che guadagni e perdite non sono certi, ma soggetti a rischio e dobbiamo fare spazio alle probabilità. A differenza della teoria classica che si limita a moltiplicare l'utilità
Le
Qui sotto gli andamenti delle
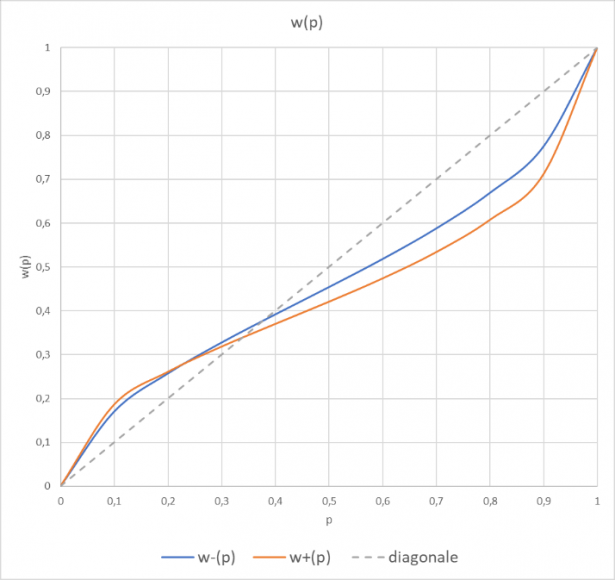
Dove si vede che per valori piccoli di
In definitiva la teoria di TK esprime l'utilità come \prodotto di due funzioni;
Infine, per distinguere l'utilità classica
Il modello completo di utilità proposto da TK, tenendo conto dei parametri di fitting dei dati sperimentali è il seguente (R4]):
Un esempio della funzione di utilità attesa secondo la Prospect Theory è riportato nel seguente diagramma
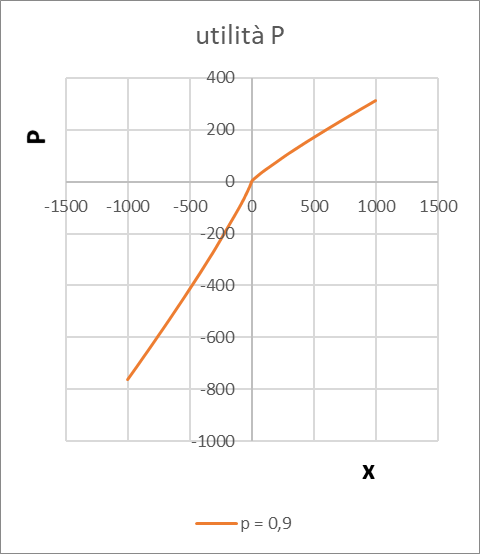
Si vede chiaramente che il ramo negativo (perdita) ha pendenza nettamente superiore al ramo positivo (guadagno); questo è ben evidente nel diagramma inferiore che riporta la
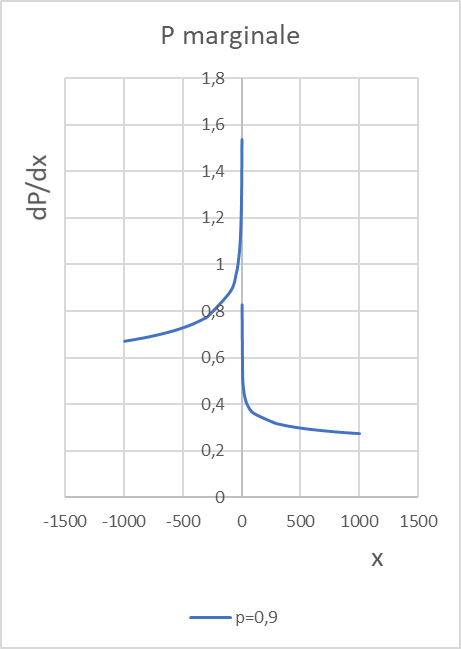
Dal diagramma della
Il fatto che la funzione
Il diagramma completo delle correlazioni
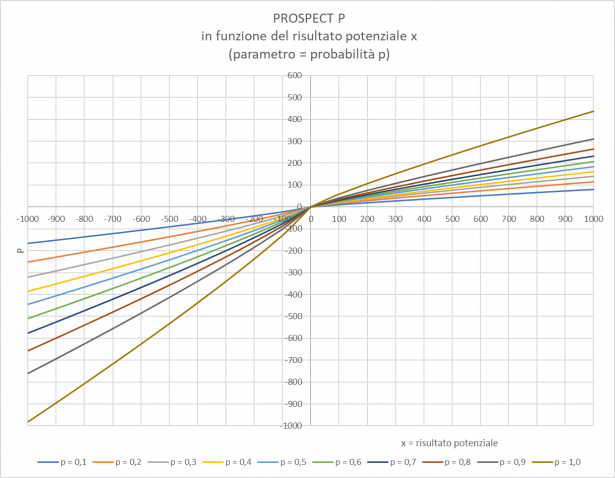
Dove la variabile indipendente
Per un'introduzione storico-scientifica ed una chiara sintesi dei vari aspetti della teoria TK si consiglia l'articolo di Roberto Chiappi (R7) pubblicato su Matematicamente.it. Mentre per uno studio approfondito si possono consultare i libri (R8, R9, R10) riportati nei RIFERIMENTI.
La Prospect Theory, frutto di molti anni di riflessione e lavoro collaborativo da parte dei due abili psicologi, ha creato un nuovo campo di indagine economica, l'economia comportamentale. Per questi risultati nel 2002 Daniel Kahnemann ha ottenuto, insieme all'economista Vernon Smith, il premio Nobel per l'economia (Amos Tversky era scomparso alcuni anni prima, con grande rimpianto da parte dell'amico/collega).
Il mondo degli studiosi non è certo rimasto indifferente a questa nuova e rivoluzionaria teoria dell'utilità e vi sono stati diversi studi sperimentali per convalidare-falsificare la teoria. In particolare vogliamo citare un articolo del 2013 di autori slovacchi (R5]) che hanno replicato i test e rifittato i parametri della teoria. Nel loro articolo è presente un'ampia tabella riassuntiva dei parametri delle loro indagini, accanto a quelli degli studi di altri dieci ricercatori pubblicate nel periodo 1992-2013. In sostanza i parametri delle varie ricerche, pur essendo un po' diversi tra di loro, sono piuttosto ben allineati in intervalli di limitata dimensione. La variabilità dei valori dei parametri è pienamente giustificata dalla diversità dei test ed anche dalla diversità statistica del campione di persone partecipanti ai test. La Prospect Theory è dunque solida e credibile.
Proviamo ora a vedere qualche applicazione a casi pratici, che ci aiuteranno a capire la logica della teoria e la sua applicazione.
Ci rendiamo conto che paragonare il guadagno atteso
Esempio 1
Ad una persona vengono proposte due alternative:
A: vincita certa (p=1) di 600
B: vincita di 1000 con p = 0.6 o vincita nulla con p = 0.4
Dal punto di vista della teoria classica le due alternative si equivalgono e il guadagno vale
Mentre secondo la Prospect Theory si ottiene il risultato di questo diagramma:
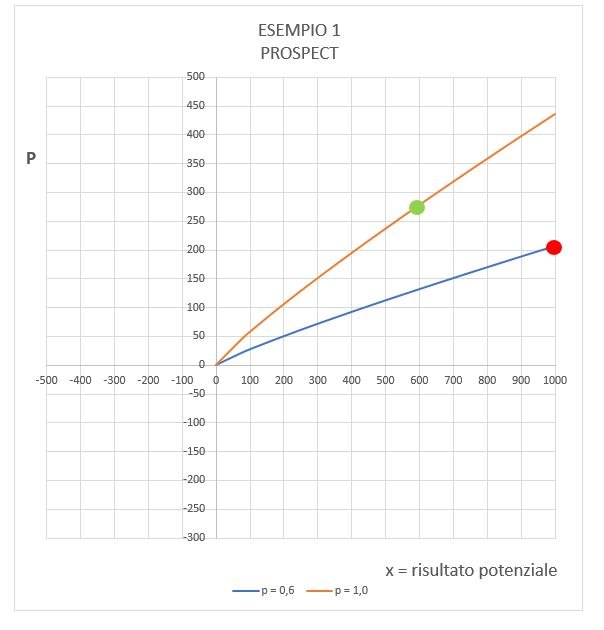
Dove si vede che l'alternativa certa (A, punto verde) l'utilità vale 278, mentre per l'altra (B, punto rosso) l'utilità vale 207. Conclusione: la certezza è preferita.
Esempio 2
Consideriamo lo stesso problema capovolto. Qui non ci sono guadagni, ma solo perdite.
A: perdita certa (p=1) di 600
B: perdita di 1000 con p=0.6 oppure nessun perdita con p=0,4
Anche in questo caso per la teoria classica le due situazioni si equivalgono
Ma secondo la Prospect è ben diverso, come appare sotto:
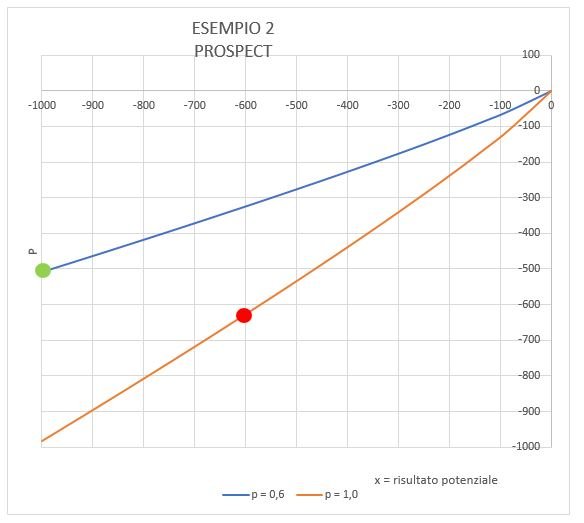
Si vede molto chiaramente che in termini di utilità l'alternativa rischiosa B (verde), che vale -509 è di gran lunga preferita alla alternativa certa A (rosso) che vale -626.
Mettendo insieme i risultati degli esempi 1 e 2 si conclude che, a pari bilancio economico, in caso di guadagno il giocatore preferisce la certezza, mentre in caso di perdita preferisce correre il rischio, nella speranza di ridurre la perdita.
Esempio 3
In questo caso ci sono due scommesse alternative.
A: guadagno 800 con p =0.2 vs guadagno nullo con p=0.8
B: guadagno 200 con p = 0.8 vs guadagno nullo con p=0.2
In termini di guadagno atteso abbiamo:
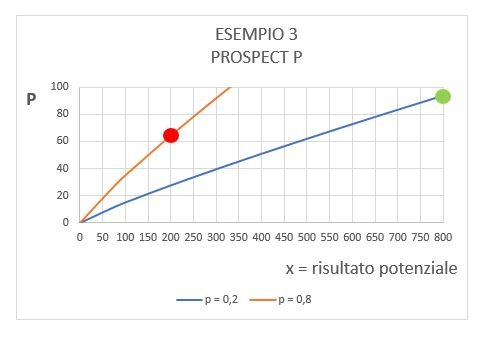
Come avviene un fatto del genere? Perché la teoria prevede, in linea con i dati sperimentali, che a bassi valori di p risulta (w(p) \gt p), mentre ad alti valori di
Esempio 4
Qui abbiamo un giocatore che prima partecipa ad una scommessa con guadagno e immediatamente dopo ad una scommessa con perdita.
A: guadagno 500 con p=0.5 vs guadagno nullo con p=0.5
B: perdita 500 con p=0.5 vs perdita nulla con p=0.5
Secondo la teoria classica
Secondo la Prospect il risultato è ben diverso ed è visualizzato da seguente grafico
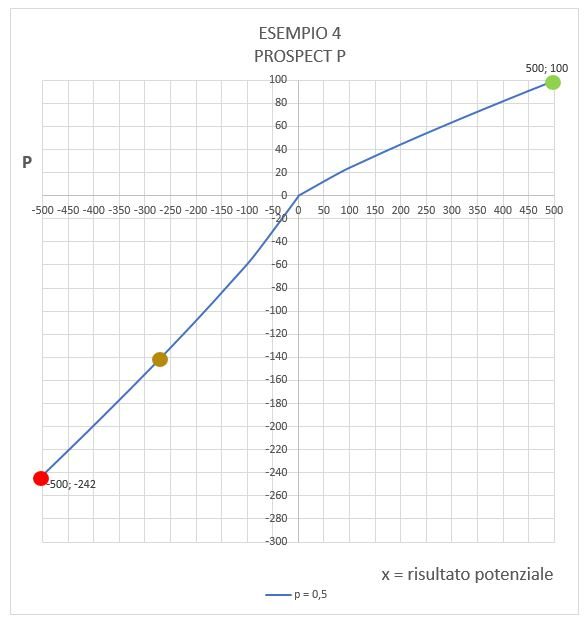
Lo step A (punto verde) vale
Tutti i calcoli sono riportati nel file EXCEL associato all'articolo.
APPENDICE
È forse un caso ma la struttura della Prospect Theory è compatibile con le funzioni di utilità di Cobb-Douglas. La funzione proposta da questi autori, che si applica a diversi campi dell'economia, ha la seguente forma (R11):
Nel caso dell'utilità
Che sostanzialmente coincide con la funzione
RIFERIMENTI
- (R1) (articolo di Bernoulli ristampato da Econometrica)
- (R2) (teoria utilità di Bernoulli)
- (R3) Daniel Kanheman and Amos Tversky - An Analysis of Decision under Risk- Econometrica - 47(2) 263-291, 1979
- (R4) Amos Tversky and Daniel Kanheman - Advances in Prospect Theory: Cumulative representation of uncertainty- Journal of Risk and Uncertainty, 5(4): 297-323, 1992
- (R5) Autori slovacchi: Testing Prospect Theory parameters
- (R6) voce "utility" dell'Enciclopedia filosofica di Stanford
- (R7) Roberto Chiappi - Le perdite sono percepite con intensità doppia dei guadagni: Prospect Theory [Daniel Kahneman]
- (R8) Economia Emotiva (che cosa si nasconde dietro i nostri conti quotidiani)- M. Motterlini, Rizzoli 2006.</a>
- (R9) Pensieri lenti e veloci - D. Kahneman, Oscar Saggi, 2017
- (R10) Un amicizia da Nobel - M. Lewis, Cortina, 2017
- (R11) (utilità di Cobb-Douglas) utilità di Cobb-Douglas
PROSPECT THEORY
parametri da articolo T-K di Journal of Risk and Uncertainty, 5:297-323 (1992) http://psych.fullerton.edu/mBIRNBAUM/psych466/articles/Tversky_Kahneman_JRU_92.pdf
VALORE PERCEPITO DEL RISULTATO POTENZIALE
x v(x) 0,88
α
24 -10000 -7450,5 2,25
λ
23 -9583 -7176,6
22 -9167 -6901,3 xmin -10000 limite superiore x ( ad libitum)
21 -8750 -6624,4 xmax 15000 limite inferiore x ( ad libitum)
20 -8333 -6346,0
19 -7917 -6066,0
18 -7500 -5784,1
17 -7083 -5500,4
16 -6667 -5214,6
15 -6250 -4926,7
14 -5833 -4636,5
13 -5417 -4343,8
12 -5000 -4048,3
11 -4583 -3749,9
10 -4167 -3448,2
9 -3750 -3142,9
8 -3333 -2833,5
7 -2917 -2519,3
6 -2500 -2199,7
5 -2083 -1873,7
4 -1667 -1539,6
3 -1250 -1195,3
2 -833 -836,6
1 -1,0 -2,3
0 0,0
1 1 1,0
2 1200 512,5
3 1800 732,2
4 2400 943,2
5 3000 1147,8
6 3600 1347,6
7 4200 1543,3
8 4800 1735,8
9 5400 1925,3
10 6000 2112,4
11 6600 2297,2
12 7200 2480,0
13 7800 2661,0
14 8400 2840,3
15 9000 3018,1
16 9600 3194,5
17 10200 3369,5
18 10800 3543,3
19 11400 3716,0
20 12000 3887,6
21 12600 4058,1
22 13200 4227,7
23 13800 4396,4
24 14400 4564,1
25 15000 4731,1
PROBABILITA' PESATA 0,69
γneg 0,61
γpos
diagonale
p w-(p) w+(p)
0 0 0 0
0,1 0,1701454281
0,1863025664 0,1
0,2 0,2570254668
0,2607631828 0,2
0,3 0,3275756392
0,3183675836 0,3
0,4 0,3916537101
0,370023098 0,4
0,5 0,4539875495
0,4206393543 0,5
0,6 0,5180900046
0,4738539475 0,6
0,7 0,5877810482
0,5338198025 0,7
0,8 0,6689559956
0,6074392743 0,8
0,9 0,7749034872
0,7117160639 0,9
1 1 1 1
PROSPECT VALUE 0,88
α 2,25
λ 0,69
γneg 0,61
γpos
xmin -1000
xmax 1000
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 p
0,17014542810,2570254668
0,3275756392
0,3916537101
0,4539875495
0,5180900046
0,5877810482
0,6689559956
0,7749034872 1 w-(p)
0,18630256640,2607631828
0,3183675836
0,370023098
0,4206393543
0,4738539475
0,5338198025
0,6074392743
0,7117160639 1 w+(p)
PROSPECT VALUE P derivata
x v(x) p = 0,1 p = 0,2 p = 0,3 p = 0,4 p = 0,5 p = 0,6 p = 0,7 p = 0,8 p = 0,9 p = 1,0 p=0,9
24 -1000 -982,1606225
-167,1101396 -252,4402924
-321,7318937
-384,6668517
-445,8886943
-508,8476015
-577,2954002
-657,0222371
-761,0796914 -982,1606225 0,6697501285
23 -958 -946,0566027
-160,9672057 -243,1606399
-309,9050964
-370,5265784
-429,4979188
-490,1424697
-556,0741416
-632,8702366
-733,1025606 -946,0566027 0,6731793948
22 -917 -909,7636586
-154,7921271 -233,832429
-298,016412
-356,3123122
-413,021374
-471,3394581
-534,7418368
-608,591854
-704,9790316 -909,7636586 0,6767798704
21 -875 -873,2721394
-148,583262 -224,4531792
-286,0626793
-342,0202733
-396,4546786
-452,4335667
-513,2928134
-584,1806334
-676,7016261 -873,2721394 0,6805684925
20 -833 -836,5714162
-142,3388017 -215,0201587
-274,0404164
-327,6462989
-379,7930072
-433,4192889
-491,7208238
-559,6294646
-648,2621077 -836,5714162 0,6845647857
19 -792 -799,6497287
-136,0567454 -205,5303448
-261,945771
-313,185783
-363,0310208
-414,2905316
-470,0189557
-534,9304804
-619,6513633 -799,6497287 0,6887914102
18 -750 -762,4939988
-129,7348678 -195,9803759
-249,774459
-298,6336035
-346,162782
-395,0405193
-448,1795218
-510,0749321
-590,8592586 -762,4939988 0,6932748635
17 -708 -725,0896003
-123,3706804 -186,366493
-237,5216893
-283,9840321
-329,1816508
-375,6616743
-426,1939252
-485,0530355
-561,8744598 -725,0896003 0,6980463877
16 -667 -687,4200739
-116,9613827 -176,6844653
-225,1820701
-269,2306223
-312,0801548
-356,1454692
-404,0524915
-459,8537799
-532,6842124 -687,4200739 0,7031431604
15 -625 -649,4667672
-110,5038011 -166,929499
-212,7494914
-254,3660689
-294,8498261
-336,4822404
-381,7442571
-434,4646878
-503,2740627 -649,4667672 0,7086098803
14 -583 -611,2083755
-103,9943107 -157,096118
-200,2169743
-239,3820279
-277,4809926
-316,6609501
-359,2566996
-408,8715073
-473,6275016 -611,2083755 0,7145009167
13 -542 -572,6203465
-97,42873398 -147,1780118
-187,576476
-224,2688832
-259,9625079
-296,668878
-336,5753875
-383,057814
-443,7255034 -572,6203465 0,7208832793
12 -500 -533,6740946
-90,80220727 -137,1678333
-174,8186326
-209,0154391
-242,2813944
-276,4912141
-313,6835187
-357,0044853
-413,5459169 -533,6740946 0,7278408138
11 -458 -494,3359422
-84,10900051 -127,0569263
-161,9324123
-193,6085058
-224,4223631
-256,1105106
-290,5612983
-330,6889924
-383,0626455 -494,3359422 0,7354802794
10 -417 -454,5656615
-77,34226906 -116,8349513
-148,9046371
-178,0323278
-206,3671507
-235,5059256
-267,185081
-304,0844246
-352,2445162 -454,5656615 0,7439404183
9 -375 -414,3144055
-70,49370187 -106,4893534
-135,7193062
-162,267774
-188,0935817
-214,6521522
-243,5261555
-277,1581056
-321,0536776 -414,3144055 0,7534059634
8 -333 -373,5216797
-63,55300609 -96,00458408
-122,356603
-146,2911517
-169,5741921
-193,5178488
-219,5489644
-249,8695672
-289,4432522 -373,5216797 0,7641301858
7 -292 -332,1107249
-56,50712146 -85,3609141
-108,791383
-130,0723976
-150,7741342
-172,063247
-195,20839-222,1674607
-257,3537589 -332,1107249 0,7764730554
6 -100 -129,4739859
-22,02940676 -33,27811166
-42,41252369
-50,70896693
-58,77957759
-67,07917795
-76,10235514
-86,61239915
-100,3298432 -129,4739859 0,88290262
5 -50 -70,35194713
-11,97006216 -18,08224205
-23,04558405
-27,5536011
-31,93890808
-36,44864062
-41,35154123
-47,06235684
-54,51596917 -70,35194713 0,9594810574
4 -30 -44,87962529
-7,636063057 -11,53520664
-14,70147194
-17,57727175
-20,37479111
-23,25168527
-26,3793932
-30,02249442
-34,77737814 -44,87962529 1,020136426
3 -15 -24,38612671
-4,149187968 -6,2678556-7,988301045
-9,550917 -11,07099791
-12,6342085
-14,33370312
-16,31324567
-18,89689463 -24,38612671 1,108617818
2 -5 -9,274192838
-1,57796151 -2,383703743
-3,037999647
-3,632272033
-4,21036808
-4,80486661
-5,451194787
-6,204026904
-7,186604371 -9,274192838 1,264842369
1 -1,0 -2,25 -0,3828272132-0,5783073002
-0,7370451882
-0,8812208476
-1,021471986
-1,16570251
-1,322507358
-1,50515099
-1,743532846 -2,25 1,534308905
0 0 0 0 0 0 0 0 0 0 0 0
1 0,1 0,1318256739
0,024559461350,03437528229
0,04196902125
0,04877854423
0,05545106634
0,06246611594
0,07037115518
0,08007609166
0,093822449720,1318256739 0,8256375575
2 5 4,121863484
0,76791374521,074830241
1,312267717
1,525184696
1,733817994
1,953161283
2,200332351
2,503781763
2,933596454 4,121863484 0,516312976
3 15 10,83827854
2,019199107 2,826224008
3,450556549
4,010413401
4,559006486
5,135761069
5,785687708
6,583596057,713776941 10,83827854 0,4525415805
4 30 19,94650013
3,716084164 5,20131286
6,350319048
7,380665771
8,390282936
9,451727825
10,64783676
12,11628756
14,19624456 19,94650013 0,4164231738
5 50 31,26753206
5,825221467 8,153421179
9,954568628
11,56970908
13,1523545
14,81624349
16,69122779
18,99312698
22,25360484 31,26753206 0,3916634453
6 100 57,54399373
10,72059371 15,00535496
18,32014224
21,29260683
24,20526837
27,26744858
30,71812337
34,954481840,95498472 57,54399373 0,3604038655
7 280 142,3964189
26,52881829 37,13174343
45,33440382
52,68996408
59,89753772
67,47510522
76,01402823
86,49717739
101,3458188 142,3964189 0,3185154305
8 320 160,1518578
29,83670212 41,76170817
50,98715998
59,25988656
67,36617406
75,88859001
85,49223309
97,28252828
113,9826498 160,1518578 0,3134522871
9 360 177,6422236
33,09520215 46,32255163
56,55552547
65,7317259
74,72331023
84,17646888
94,8289367
107,9068634
126,4308241 177,6422236 0,3090531257
10 400 194,9004278
36,31044989 50,82285589
62,04997825
72,11766009
81,98279011
92,35433708
104,0417079
118,3901744
138,7137653 194,9004278 0,3051702837
11 440 211,9524082
39,48727759 55,26938456
67,47877603
78,42728669
89,15552412
100,4344853
113,1443927
128,748217150,8499337 211,9524082 0,3016998673
12 480 228,8191083
42,62958712 59,66759898
72,84858661
84,66835533
96,25032199
108,4268377
122,1481712
138,9937131
162,8542351 228,8191083 0,2985660977
13 520 245,5177766
45,74059186 64,02199686
78,16490126
90,84724828
103,274439
116,3395676
131,062251
149,13714174,7389455 245,5177766 0,2957120617
14 560 262,0628524
48,82298196 68,3363435
83,43231708
96,96930851
110,233949
124,1795171
139,8943401
159,1872689
186,5143418 262,0628524 0,2930939657
15 600 278,4665924
51,87904081 72,61383494
88,65473614
103,0390712
117,1340076
131,952494
148,6509813
169,1515448198,189147 278,4665924 0,2906774157
16 640 294,7395235
54,91072965 76,85721626
93,83550991
109,0604316
123,9790429
139,6634867
157,3377942
179,0363623
209,7708536 294,7395235 0,2884349236
17 680 310,8907805
57,91975027 81,06886944
98,97754656
115,0367697
130,7728972
147,3168236
165,959655
188,8472701
221,2659626 310,8907805 0,2863441869
18 720 326,9283607
60,90759263 85,2508799
104,0833922
120,9710448
137,5189346
154,9162943
174,5208329
198,5891262
232,6801661 326,9283607 0,2843868696
19 760 342,8593214
63,87557148 89,40508791
109,1552937
126,8658683
144,2201236
162,4652429
183,0250952
208,2662174
244,0184867 342,8593214 0,2825477214
20 800 358,6899335
66,82485515 93,53312871
114,1952474
132,7235604
150,879102
169,9666409
191,4757895
217,8823529
255,2853876 358,6899335 0,2808139264
21 840 374,4258046
69,75648832 97,63646455
119,2050387
138,5461962
157,4982287
177,4231456
199,8759091
227,440939266,4848599 374,4258046 0,2791746151
22 880 390,07197772,67141039 101,7164103
124,1862728
144,3356414
164,0796246
184,8371461
208,2281457
236,9450387
277,6204921 390,071977 0,2776204921
23 920 405,63300875,5704704 105,7741542
129,1404006
150,0935823
170,6252066
192,2108021
216,5349322
246,39742288,6955278 405,633008 0,2761435484
24 960 421,1130354
78,45443923 109,8107754
134,0687395
155,82155177,1367153
199,5460742
224,7984774
255,8005966299,712912 421,1130354 0,274736836
25 1000 436,5158322
81,32401981 113,8272578
138,9724907
161,5209406
183,6157378
206,8447502
233,0207953
265,1568604
310,6753299 436,5158322 0,2733942904
ESEMPIO 1 Guadagno certo di 750
x 600
p 1 probabilità 0,88
α
v(x) 278,467 2,25
λ
0,61 0,69
γneg
γ
w(p) 1,00 0,61
γpos
P2 278 Prospect value xmin -1000
Guadagno di 1000 con p=25% e di nulla con p = 75% xmax 1000
x 1000
p 0,6 probabilità
v(x) 436,516
0,61
γ
w(p) 0,47
P1 207 Prospect value
0,6 1,00
x v(x) p = 0,6 p = 1,0
0 0 0 0
1 0,1 0,1318256739
0,06246611594
0,1318256739
2 80 47,28454219
22,40596697
47,28454219
3 120 67,55842193
32,01282492
67,55842193
4 160 87,02130358
41,23538822
87,02130358
5 200 105,9025448
50,1823389
105,9025448
6 240 124,3328511
58,9156123
124,3328511
7 280 142,3964189
67,47510522
142,3964189
8 320 160,1518578
75,88859001
160,1518578
9 360 177,6422236
84,17646888
177,6422236
10 400 194,9004278
92,35433708
194,9004278
11 440 211,9524082
100,4344853
211,9524082
12 480 228,8191083
108,4268377
228,8191083
13 500 237,1884865
112,3927006 237,2
14 560 262,0628524
124,1795171
262,0628524
15 600 278,4665924
131,952494
278,4665924
16 640 294,7395235
139,6634867
294,7395235
17 680 310,8907805
147,3168236
310,8907805
18 720 326,9283607
154,9162943
326,9283607
19 750 338,8862217
160,5825739
338,8862217
20 800 358,6899335
169,9666409
358,6899335
21 840 374,4258046
177,4231456
374,4258046
22 880 390,071977
184,8371461
390,071977
23 920 405,633008
192,2108021
405,633008
24 960 421,1130354
199,5460742
421,1130354
25 1000 436,5158322
206,8447502
436,5158322
ESEMPIO 3
ESEMPIO 2 Perdita certa di 750 0,88
α
x -600 2,25
λ
p 1 probabilità 0,69
γneg
v(x) -626,550 0,61
γpos
0,69
γ
w(p) 1,00 xmin -1000
P1 -626,5 Prospect value xmax 1000
perdita di 1000 con P = 25% e nulla con p = 75%
x -1000
p 0,6 probabilità
v(x) -982,161
0,69
γ
w(p) 0,52
P2 -508,8 Prospect value
0,6 1,00
x v(x) p = 0,6 p = 1,0
24 -1000 -982,1606225
-508,8476015 -982,1606225
23 -958 -946,0566027
-490,1424697 -946,0566027
22 -917 -909,7636586
-471,3394581 -909,7636586
21 -875 -873,2721394
-452,4335667 -873,2721394
20 -833 -836,5714162
-433,4192889 -836,5714162
19 -792 -799,6497287
-414,2905316 -799,6497287
18 -750 -762,4939988
-395,0405193 -762,4939988
17 -708 -725,0896003
-375,6616743 -725,0896003
16 -667 -687,4200739
-356,1454692 -687,4200739
15 -600 -626,5498328
-324,6092058 -626,5498328
14 -583 -611,2083755
-316,6609501 -611,2083755
13 -542 -572,6203465
-296,668878 -572,6203465
12 -500 -533,6740946
-276,4912141 -533,6740946
11 -458 -494,3359422
-256,1105106 -494,3359422
10 -417 -454,5656615
-235,5059256 -454,5656615
9 -375 -414,3144055
-214,6521522 -414,3144055
8 -333 -373,5216797
-193,5178488 -373,5216797
7 -292 -332,1107249
-172,063247 -332,1107249
6 -250 -289,9811219
-150,2363208 -289,9811219
5 -208 -246,9961758
-127,9662499 -246,9961758
4 -167 -202,9595156
-105,1512964 -202,9595156
3 -125 -157,5662973
-81,6335237 -157,5662973
2 -83 -110,2815907
-57,13578981 -110,2815907
1 -1,0 -2,25 -1,16570251 -2,25
0 0 0 0
ESEMPIO 3 Guadagno 800 con p=20% vs guadagno nullo con p=80% 0,88
α
x 800 2,25
λ
p 0,2 probabilità 0,69
γneg
v(x) 358,690 0,61
γpos
0,61
γ
w(p) 0,26 xmin -1000
P2 94 Prospect value xmax 1000
