Qualcosa di simile a quello che farebbero le industrie farmaceutiche e quelle alimentari quando anticipano volutamente le scadenze dei loro prodotti.
Su tutto questo non vi è oggi alcuna certezza e l'articolo non entra nell'acceso dibattito in corso. Si propone però di cercare di chiarire termini come "usura fisica", "obsolescenza tecnologica", "convenienza economica", "innovazione".
Una azienda può fare investimenti in mezzi di produzione per sostituire impianti usurati, mal funzionanti, tecnologicamente obsoleti o economicamente superati. In tutti questi casi l'obiettivo è sempre quello di mantenere la capacità/qualità produttiva della azienda al livello corrente producendo gli stessi prodotti per gli stessi mercati. Altri tipi d'investimento implicano la netta espansione della capacità produttiva delle linee esistenti o nuove linee per diversi prodotti/mercati.
Gli investimenti per l'espansione delle capacità produttive relative ai prodotti consueti, o per lo sviluppo di nuovi derivano tipicamente da proposte formulate dalla pianificazione strategica, dai gruppi di marketing o dalla ricerca e sviluppo. L'analisi degli investimenti in espansione/modifica delle capacità produttive generalmente esula dalle competenze dei responsabili delle attività correnti di una azienda ed implica il coinvolgimento dell'alta direzione e l'utilizzo di tecniche probabilistiche e di analisi dei rischi.
I due tipi di investimento dunque differiscono in alcuni aspetti significativi. Il mantenimento della capacità è generato dalla continuazione di una attività in cui l'azienda ha una considerevole esperienza, un notevole insieme di dati storici e una struttura/maestranze in grado di valutare l'adeguatezza/inadeguatezza degli impianti in essere. Inoltre, in assenza di specifici segnali di cambiamento, la previsione secondo cui la domanda dei prodotti dell'azienda continuerà allo stesso livello è molto più prudente e meno aleatoria di quella di una espansione della domanda. Dunque un investimento per il mantenimento della capacità produttiva sarà generalmente meno soggetto all'incertezza di quelli implicati dalla produzione di volumi maggiori o addirittura di nuovi prodotti.
Inoltre la produzione attraverso macchinari ed impianti è il cuore stesso di una organizzazione manifatturiera e taluni investimenti di sostituzione sono necessari a meno che uno stabilimento non voglia cessare la sua attività. Al contrario i piani di espansione/conversione possono essere sviluppati indipendentemente e compatibilmente con le attività correnti dell'impresa; per questo motivo spesso gli investimenti per il mantenimento delle capacità, essendo argomento di inderogabili necessità, possono diventare decisioni di routine che non richiedono sempre l'intervento dei livelli più elevati di management.
In questo articolo ci occuperemo dei programmi di sostituzione degli impianti al fine di mantenere intatte le capacità produttive in essere.
La decisione circa il tempo più adatto per la sostituzione di una macchina gioca un ruolo essenziale nello sviluppo del progresso tecnologico ed economico di una azienda ed ha un rilevante effetto indotto nei settori produttivi impegnati nella fabbricazione dei nuovi impianti. Quando le aziende iniziano a differire la sostituzione dei loro impianti, il risultato immediato è un declino nella quantità e qualità della produzione, che a sua volta porta alla disoccupazione ed è spesso indice di un processo di recessione della economia. Le conseguenze di una inadeguata politica di sostituzione sono potenzialmente disastrose: se la sostituzione viene procrastinata oltre un ragionevole tempo, i costi di produzione tenderanno a salire, mentre quelli dei concorrenti, che impiegano macchinari più moderni diminuiscono, così l'azienda non è più in grado di sostenere la competizione dei prezzi e si trova nell'impossibilità di coprire i costi e ottenere i fondi dalle banche con i quali sostituire le vecchie macchine; si crea una specie di trappola tecnologica ed economica che porta alla chiusura delle linee più improduttive, alla cassa integrazione per i dipendenti o addirittura al fallimento dell'azienda.
Gli impianti si suddividono solitamente in due categorie: quelli che improvvisamente si deteriorano (come ad esempio le lampadine elettriche) e quelli soggetti ad un deterioramento graduale durante la loro vita (come le macchine utensili): di questo secondo tipo di impianti ci occuperemo nel seguito.
Valori di recupero e tassi d'interesse nulli
Si può semplicemente sintetizzare il problema: "Quale è la durata media di un impianto che rende minimo il costo medio annuo per l'intero periodo di utilizzazione?"Evidentemente, una volta che l'impianto sia stato acquisito, è chiaro che maggiori sono gli anni di utilizzo e maggiori sono i periodi di servizio su cui è possibile ripartire il costo iniziale di acquisizione. Il problema è significativo perché esistono altri costi (esercizio e manutenzione) che crescono con l'età degli impianti. Si avrà dunque un Costo totale, in funzione degli anni, formato da una componente decrescente (Investimento annuo medio) ed una crescente (Esercizio e manutenzione). Da qui l'origine del Costo annuo medio, somma dei due, che solitamente presenta un minimo. Per trovare ed utilizzare questo minimo si può formulare la seguente tattica: "Sostituire alla fine di qualsiasi periodo per il quale i costi di esercizio e manutenzione del periodo successivo superano il costo medio fine al tempo di sostituzione, e non sostituire finché i costi di esercizio e manutenzione di un periodo non eccedono il costo medio alla fine del periodo".. Se interpretiamo i costi di esercizio e manutenzione come il costo marginale per ottenere il servizio dell'impianto nel periodo n, dato che esso ha servito nel periodo n-1, la tattica apparirà come l'applicazione di un noto principio dell'economia: il costo medio diminuirà finché il costo marginale è inferiore ad esso, e quando il costo marginale eccede il costo medio, quest'ultimo comincerà a salire.
Gli economisti chiamano Costo marginale (Cm) il costo di una unità prodotta in più: dunque Cm = DC/1. Il concetto è molto simile a quello di derivata dei matematici ma, come vedremo negli esempi numerici, non coincide con esso. Per comprendere cosa gli economisti intendono per Costo medio e marginale si può osservare che: " se ad un gruppo di n numeri di cui abbiamo calcolato la media aggiungiamo un numero n+1, la nuova media sarà maggiore alla precedente a seconda che il nuovo numero n+1 sia maggiore o minore della vecchia media".
Per chiarire questi concetti vediamo un semplice esempio numerico che prevede di acquistare una macchina Investendo I = 1000
| Costo iniz. Inv. (I) = | 1000 | $ | |
| Costo Eser + Manut: | Cn | ||
| anno1 | 50 | $ | |
| anno2 | 110 | $ | |
| anno3 | 180 | $ | |
| anno4 | 260 | $ | |
| anno5 | 350 | $ | |
| anno6 | 450 | $ | |
| anno7 | 650 | $ | |
| Totale | 2050 | $ |
Tutti i calcoli necessari per stabilire la durata ottimale in anni della macchina possono essere riassunti facilmente su foglio elettronico:
| Costi ([math]): | Col.1 + Col.4 | |||||
| Col.1 | Col.2 | Col.3 | Col.4 | Col.5 | Col.6 | |
| Anno | Cost. med. I | C. Marg. | Progr. | Media | Costo | Derivata |
| (n) | (I/n) | Es.+ Man. | Es+Man. | Es.+Man. | Medio Tot. | Cost.Med. |
| 0 | ||||||
| 1 | 1000 | 50 | 50 | 50 | 1050 | |
| 2 | 500 | 110 | 160 | 80 | 580 | -470 |
| 3 | 333 | 180 | 340 | 113 | 447 | -133 |
| 4 | 250 | 260 | 600 | 150 | 400 | -47 |
| 5 | 200 | 350 | 950 | 190 | 390 | -10 |
| 6 | 167 | 450 | 1400 | 233 | 400 | 10 |
| 7 | 143 | 650 | 2050 | 293 | 436 | 36 |
Col.1 Riporta il Costo dell'Investimento diviso il numero n degli anni di vita della macchina (Costo annuo medio dell'Investimento).
Col.2 Riporta i Costi di Esercizio e Manutenzione annui preventivati [math]Cn[/math]
Col.3 Riporta i Costi di Esercizio e Manutenzione progressivi (o cumulati),
Col.4 Riporta i Costi medi annui di Esercizio e Manutenzione,
Col.5 Riporta i Costi medi annui Totali,
Col.6 Riporta la Derivata, approssimata numericamente dal rapporto incrementale, del Costo Medio Totale rispetto agli anni di vita della macchina,
Poiché
Consideriamo per iniziare le Colonne 1, 4 e 5 che riportano rispettivamente i costi medi annui dell'investimento (decrescenti con il crescere del numero degli anni), i costi medi di esercizio e manutenzione (crescenti con il numero degli anni) ed i costi medi totali somma dei due precedenti. Vediamone il grafico:

Appare evidente, come si poteva già evincere dalla tabella numerica che il costo medio totale presenta un minimo alla fine del 5° anno.
Consideriamo ora il grafico delle Colonne 5 e 6 che riportano ancora il costo medio totale e la sua derivata:
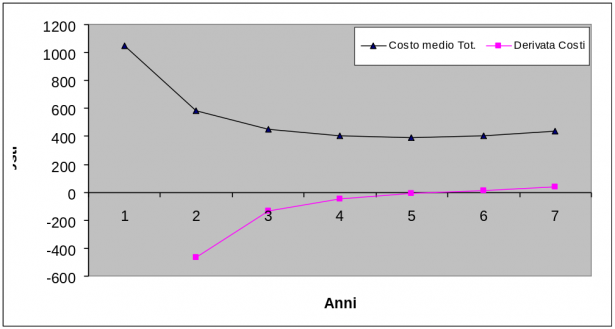
Si può notare, come insegna la matematica, che alla fine del 5° anno, lo abbiamo già osservato, il costo medio totale presenta un minimo e, in corrispondenza di esso, la sua derivata si annulla passando da valori negativi a positivi.
Prendiamo infine in considerazione le colonne 5 e 2 che riportano oltre al consueto costo totale il costo di esercizio e manutenzione che, come abbiamo detto può essere assimilato ad un costo marginale dovuto all'utilizzo della macchina per un ulteriore anno. Ecco il grafico:
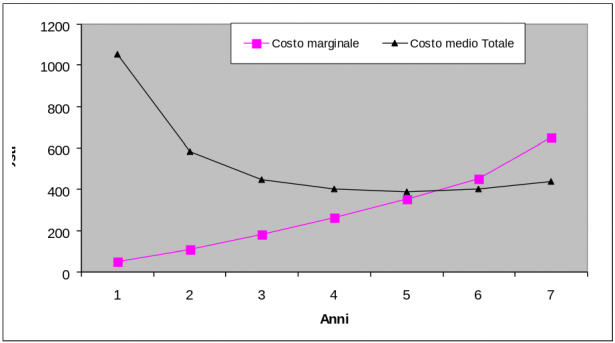
Si può osservare che, come insegnano gli economisti, la curva del "costo marginale" interseca quella del "costo medio" nel punto di minimo di quest'ultimo.
In definitiva si è stabilito che la fine del 5° anno è il momento migliore (durata ottimale) per sostituire la macchina. Lo abbiamo stabilito con l'aiuto della matematica, della economia e del buon senso.
Interessi e valore di recupero
Si consideri ora il caso di un impianto di più grandi dimensioni e di maggiore durata, ad esempio 15 - 20 anni e oltre, come accade nelle navi e nelle piattaforme dell'industria petrolifera. In queste situazioni è necessario fare delle valutazioni sul deprezzamento del valore dell'impianto nel tempo (e quindi sull'eventuale valore di recupero ), sul tasso d'interesse e il tasso di attualizzazione, cioè il valore del denaro nel tempo.Per esemplificare consideriamo l'investimento all'anno 0 di un impianto del valore di 1 milione di [/math]. Supponiamo poi che il valore dell'impianto si dimezzi nel corso del primo anno e che poi si riduca del 10%, rispetto all'anno precedente, negli anni successivi. Dunque esprimendo i valori in milioni di $:
Col.R = Valore di recupero
Supponiamo poi che i costi di Esercizio e Manutenzione siano crescenti negli anni e forniti in input nella colonna riportata a fianco degli anni. Infine assumiamo un tasso di attualizzazione e di interesse pari al 10%.
Richiamiamo ora le formule di matematica finanziaria che ci interessano per effettuare tutti i calcoli effettuati nella tabella sottostante

(Visualizza immagine originale)
Vediamo di seguito il significato delle colonne:
Col.0 Costi di esercizio e manutenzione attualizzati al 10%
Col.1 Progressivo (o cumulata) dei Costi di esercizio e manutenzione attualizzati al 10%
Col.2 Valore di Recupero attualizzato (i = 10%)
Col.3 = Col.1 - Col.2 Costo attualizzato al netto del valore di Recupero (i = 10%)
Col.4 = Fattore di annualizzazione (al 10%): valori costanti percepiti per n anni equivalenti ad una spesa iniziale unitaria all'anno 0.
Col.5 = Col.3 * Col.4 Costi di Esercizio più Manutenzione, meno Recupero annualizzati.
Col.6 = Costo Iniziale investimento (nell'esempio 1.000.000 $) annualizzato
Col.7 = Col.5 + Col 6 Costo Totale, Ct (Investimento più esercizio più manutenzione meno recupero) annualizzati
Col.8 = Derivata, approssimata numericamente, di
Vediamo di seguito graficamente l'andamento delle principali variabili:
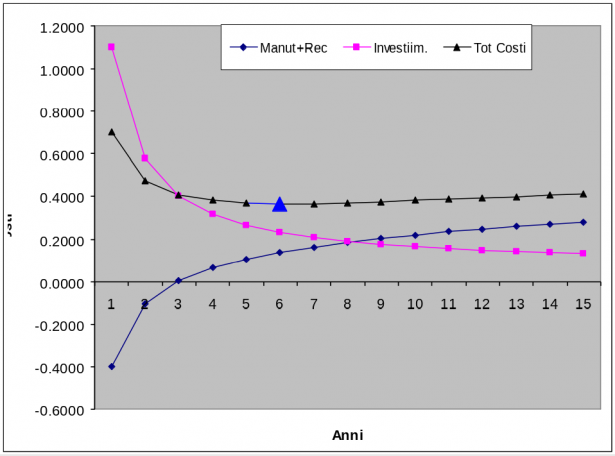
Sopra sono rappresentati gli andamenti di tre curve; Col.5: Esercizio + Manutenzione - Recupero annualizzati, curva crescente. Col.6: Investimento iniziale annualizzato, curva decrescente, Col.7 Costo totale, somma delle due curve precedenti che presenta un minimo alla fine del 6° anno.
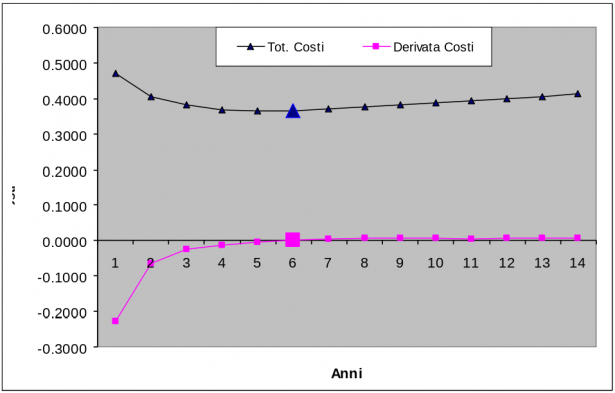
Sopra sono rappresentate due curve: Col.7 del Costo totale, rappresentata anche nel grafico precedente e la sua derivata numerica Col.8 che si azzera, come previsto dalla teoria matematica, in corrispondenza del valore minimo del Costo totale.
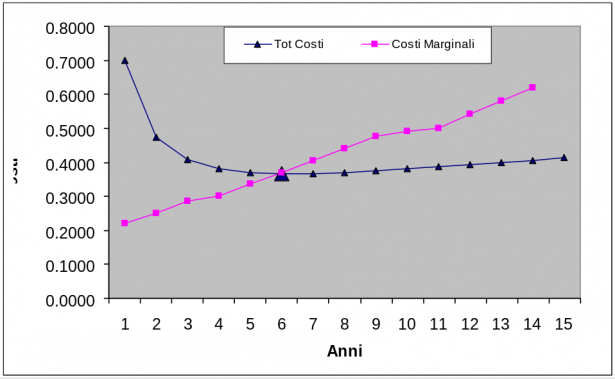
Sopra sono rappresentate due curve: Col.7 del Costo totale, rappresentata anche nel grafico precedente e il Costo Marginale Col.9 che, come previsto dalla teoria economica, interseca la curva del Costo totale medio in corrispondenza del suo valore minimo.
Avendo stabilito, in fase previsionale, che il miglior momento per la sostituzione dell'impianto è il 6° anno, in fase di gestione questo calcolo deve essere continuamente rivisto per tener conto degli effettivi costi di gestione e manutenzione, delle innovazioni introdotte nello specifico settore impiantistico (obsolescenza tecnologica) e di eventuali sgravi fiscali che favoriscano l'ammodernamento dell'impianto.
Conclusioni
Il tema della innovazione è oggi uno dei più sentiti nelle organizzazioni di ogni tipo, in particolare è assai importante il tema dell'innovazione degli impianti di produzione. In questo articolo si è affrontato il tema dell'invecchiamento degli impianti dovuti alla usura temporale. Non sostituire per tempo impianti vecchi ed inefficienti significa dover sopportare costi di esercizio e manutenzione crescenti, rischiando anche black out nella produzione. La concorrenza, dotata di impianti nuovi, potrebbe approfittarne mettendo fuori mercato le aziende poco sensibili al rinnovamento delle linee di produzione.Tema altrettanto importante, e qui non trattato, è quello della obsolescenza tecnologica degli impianti: quando conviene sostituire se esistono nuovi processi e nuovi impianti che consentono di produrre gli stessi prodotti, con la stessa o migliore qualità, e a costi inferiori?
Infine, fondamentale è la innovazione di prodotto. Se esistono nuovi prodotti, che soddisfano meglio gli stessi bisogni degli utenti/clienti, quando conviene abbandonare le vecchie produzioni per adeguarsi alle nuove richieste del mercato?
Argomenti di grande interesse non trattati in questo articolo, ma di stimolo per ulteriori pubblicazioni.
Riferimenti
- E. Levi, "Matematica finanziaria ed attuariale", Giuffrè 1964.
- E. Levi, "La scelta degli investimenti", Boringhieri 1967.
- M. Trovato, ."Matematica per le scelte economiche", Goliardica 1971.
- M. Trovato, ."Investimenti e decisioni", ISEDI 1972.
- Bonetti, Chiappi, Vitale, "La scelta degli investimenti". Tesi di laurea, Politecnico di Milano, Facoltà d'Ingegneria,1971.
- W.T Morris, "Il Sistema di decisione degli investimenti", F. Angeli, Milano 1971.
- P.Mella, "La durata ottimale di un impianto industriale" Rivista "Organiz.e Manag." 1989.
- R.Chiappi, "Il foglio elettronico come strumento per il Problem Solving", Angeli 2008.
- R.Chiappi, "Project Management, Problem Solving, Decision Making", 2015
- Calabrese, Marchet, "Esercizi per il corso di gestione degli impianti industriali", PoliMI.
- Marco M. e Roberto C., "Scelta tra Investimenti Industriali", 2016
- Hume, Smith, "Programmazione matematica", matematicamente.it, 2017


![La dinamica dei sistemi [J. W. Forrester]](https://cdn.skuola.net/shared/thumb/159x141/news_foto/images/stories/problem_solving/forrester.png)
