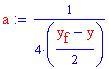_stan
di _stan
(320 punti)
4' di lettura
2,6 / 5 (8)
In questo appunto di Geometria Analitica viene data una definizione di parabola cercando di fornire sia un rappresentaizone geometrica di tale figura che una rappresentazione matematica: equazione della parabola. All'interno dell'appunto sono descritti gli elementi che compongono tale figura geometrica e alcuni esempi pratici per trovare matematicamente gli zeri e il vertice della parabola.

Parabola

Una parabola è l'insieme dei punti del piano equidistanti da un punto fisso, detto fuoco , e da una retta, detta direttrice.
Osservando l'immagine qui sotto, possiamo rendere concreta questa definizione notando come la distanza dalla punta della matita, P, al fuoco sia uguale alla distanza dello stesso punto dalla direttrice.

Se la direttrice è orizzontale, l'equazione della parabola è

[math]y = a(x - h) 2 + k[/math]
, dove:
  • Il punto (h, k) è il vertice della parabola
  • [math]a[/math]
    è una costante che determina l'orientamento
La costante
[math]a[/math]
determina l'apertura verso l'alto o verso il basso e la larghezza della parabola.

Di seguito viene proposto il grafico di una parabola definita da un fuoco e da una direttrice che presentano i valori indicati.

Per ulteriori approfondimenti sulla parabola vedi anche qua

Equazione della parabola

Di seguito sono indicate le equazioni della parabola in relazione al loro asse di simmetria:

Parabola con asse di simmetria parallelo all'asse delle y

[math]y=a\cdot x^2 +b\cdot x\cdot+ c[/math]

Parabola con asse di simmetria parallelo all'asse delle x

[math]x=a\cdot y^2 +b\cdot y + c[/math]

Fuoco

Data l'equazione della parabola con asse di simmetria parallelo all'asse y:

[math]y=a\cdot x^2+b\cdot x+c[/math]

Le coordinate del fuoco vengono espresse partendo dai coefficienti a, b, c.

[math]F (-\frac{b}{2a}, \frac{1-Δ}{4a})[/math]

con Δ che risulta uguale a

[math]Δ=b^2 -4ac[/math]

Andiamo ora a calcolare, tramite un esempio numerico pratico, le coordinate del fuoco della seguente parabola

[math]y=3\cdot x^2+4\cdot x+2[/math]

In questo specifico caso i coefficienti risultano quindi essere

[math]a=3[/math]
,
[math]b=4[/math]
,
[math]c=2[/math]
.

Partendo dalla formula per il calcolo delle coordinate del fuoco andiamo ad effettuare le relative sostituzioni dei coefficienti appena individuati:

[math]F (-\frac{b}{2a}, \frac{1-Δ}{4a}) \rightarrow F (-\frac{4}{2\cdot 3}, \frac{1-Δ}{4\cdot 3})\rightarrow F (-\frac{4}{6}, \frac{1-Δ}{12})[/math]

con

[math]Δ=b^2 -4ac \rightarrow Δ=4^2 -4\cdot3\cdot2=16-24=-8[/math]

quindi

[math]F (-\frac{2}{3}, \frac{1+8}{12}) \rightarrow F (-\frac{2}{3}, \frac{3}{4})[/math]

Equazione della direttrice

L'equazione per il calcolo della direttrice di una parabola con asse di simmetria parallelo all'asse y è la seguente:

[math]y=-\frac{1+Δ}{4a}[/math]

con Δ che risulta uguale a

[math]Δ=b^2 -4ac[/math]

Costante a

Il calcolo della costante
[math]a[/math]
viene effettuato sequendo la seguente formula:
[math]a=\frac{1}{4\cdot\frac{y_f-y}{2}}[/math]

Andando ad effettuare le rispettive sostituzioni, inserendo cioè al posto delle incognite i valori noti:

  • [math]y_f= \frac{1-Δ}{4a}[/math]
  • [math]y= -\frac{1+Δ}{4a}[/math]

Vertice

Data l'equazione della parabola
[math]y=ax^2+bx+c[/math]
, per definire le coordinate del vertice dobbiamo operare nel modo sequente:
[math](h, k)= (-\frac{b}{2a}; \frac{b}{2a})[/math]


Per ulteriori approfondimenti sul calcolo del vertice di una parabola vedi anche qua.

Gli zeri della parabola

Gli zeri di una parabola sono quei punti in cui la parabola interseca l'asse delle ascisse.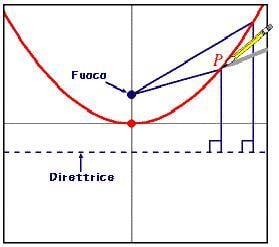 Per trovare questi valori dobbiamo porre y=0 nell'equazione della parabola
[math]y=ax^2+bx+c=0[/math]
, e andare a trovare i valori della x.

Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it