Posizioni reciproche di due circonferenze

Definizioni

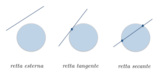
Definizione 1: Definizione di circonferenze esterne

Due circonferenze si dicono esterne se la somma dei loro raggi è strettamente minore della distanza tra i loro centri. In formule, ( OA + O'A' lt OO' ). Due circonferenze in tale posizione non hanno punti in comune.

Definizione 2: Definizione di circonferenze tangenti esternamente

Due circonferenze si dicono tangenti esternamente se la somma dei loro raggi è uguale alla distanza tra i loro centri.

In formule, ( OT + O'T = OO' ). Due circonferenze in tale posizione hanno un solo punto in comune, detto di tangenza.

Definizione 3: Definizione di circonferenze secanti

Due circonferenze si dicono secanti se la distanza dei loro centri è, al contempo, minore della somma e maggiore della differenza in valore assoluto dei loro raggi. In formule

[ |OA - O'A'| lt OO' lt OA + O'A' ]

Due circonferenze in tale posizione hanno due punti in comune, detti d'intersezione.

Definizione 4: Definizione di circonferenze tangenti internamente

Due circonferenze si dicono tangenti internamente se la differenza in valore assoluto dei loro raggi è uguale alla distanza tra i loro centri. In formule, ( | OT - O'T| = OO' ). Due circonferenze in tale posizione hanno un solo punto in comune, detto di tangenza.

Definizione 5: Definizione di circonferenze interne

Due circonferenze si dicono interne se la differenza in valore assoluto dei loro raggi è maggiore della distanza tra i loro centri. In formule, ( |OT -O'T| lt OO' ). Due circonferenze in tale posizione non hanno punti in comune.

Definizione 6: Definizione di circonferenze concentriche e coincidenti

Due circonferenze si dicono concentriche se la distanza tra i loro centri è pari a 0. Se inoltre i due raggi hanno uguale misura, le circonferenze si dicono coincidenti. Due circonferenze concentriche non coincidenti non hanno punti in comune, al contrario due circonferenze coincidenti ne hanno infiniti.

Osservazione 1: Risulta chiaro tanto dalle definizioni quanto dalle immagini che le varie posizioni reciproche di due circonferenze sono, fissati i raggi, funzione solo della distanza tra i centri. Dal momento che tutte le possibili distanze vengono coperte dalle 6 definizioni date, non è possibile disegnare due circonferenze in alcun altra posizione distinta da quelle studiate.

Osservazione 2: In virtù delle definizioni 1 - 6 e dell'osservazione 1, per capire in quale posizione si trovino due circonferenze di cui è nota l'equazione, in forma canonica o meno, è sufficiente trovarne i raggi, i centri, la distanza tra questi ultimi e confrontare i risultati ottenuti con le disequazioni che definiscono le posizioni reciproche. In particolare, non è necessario trovare i punti d'intersezione.

Determinazione dei punti d'intersezione di due circonferenze

Metodo risolutivo: Come sempre si fa in geometria analitica, per trovare le intersezioni di due curve di cui siano note le equazioni non bisogna fare altro che mettere queste ultime a sistema. Nel caso di due circonferenze, occorrerà prima portare le equazioni in forma canonica, in quanto questa operazione facilita la successiva risoluzione del sistema.

Se per esempio dovessimo trovare le intersezioni delle circonferenze ( x^2+y^2+alpha_1 x+\beta_1 y+gamma_1 = 0 ) e ( x^2+y^2+alpha_2 x +\beta_2 y + gamma_2 = 0 ), che già sono evidentemente in forma canonica, dovremmo risolvere

[ \begin{cases} x^2+y^2+alpha_1 x+\beta_1 y+gamma_1 = 0 \ x^2+y^2+alpha_2 x +\beta_2 y + gamma_2 = 0 end{cases} ]

Si potrebbe pensare che un metodo buono per risolvere questo sistema sia trovare la ? o la ? dalla prima equazione e sostituirla nella seconda, così da ottenere un'equazione nell'altra incognita; questo metodo però fallisce per vari motivi. In primo luogo, sia che scegliamo di risolverla per ? che per ?, la prima equazione (così come d'altra parte la seconda) è di secondo grado, e non ammette perciò in generale una sola soluzione. Al sostituire poi ciascuna di queste ultime nell'equazione rimanente, otterremmo delle equazioni difficili da risolvere perché di grado maggiore di 2.

Per questo motivo si applica invece sempre la strategia seguente: prima di tutto, con il metodo di sottrazione, si sostituisce una delle due equazioni, diciamo la seconda, con la differenza della prima e della seconda equazione. In questo modo otteniamo

[ \begin{cases} x^2+y^2+alpha_1 x+\beta_1 y+gamma_1 = 0 \ (x^2+y^2+alpha_1 x+\beta_1 y+gamma_1 = 0 ) - (x^2+y^2+alpha_2 x +\beta_2 y + gamma_2) = 0 end{cases} ]

[ \begin{cases} x^2+y^2+alpha_1 x+\beta_1 y+gamma_1 = 0 \ (alpha_1-alpha_2)x+(\beta_1-\beta_2)y+(gamma_1-gamma_2) = 0 end{cases} ]

Il problema adesso si è notevolmente semplificato, perché la seconda equazione è di primo grado. Potremo quindi risolverla agevolmente in una delle due incognite, diciamo ?, e sostituire il valore ottenuto, che è funzione di ?, nella prima equazione. Ciò ci restituirà un'equazione solo nella ? al più di secondo grado, che sappiamo risolvere; sostituendo i valori così ottenuti per la ? nella seconda equazione potremo ottenere anche quelli per la ?: essi costituiscono naturalmente ascisse e ordinate dei vari punti d'intersezione.

Osservazione 3: Il metodo risolutivo dimostra, tra l'altro, che due circonferenze non coincidenti hanno al più due punti d'intersezione. Infatti poiché l'equazione risolutiva nella ? è, come detto, al più di secondo grado, non potremo trovare mai più di due ascisse diverse. Si noti altresì che questo risultato non si poteva in generale ottenere seguendo il primo, erroneo, metodo risolutivo analizzato.

Esempi

Esempio 1: Si dimostri che le circonferenze ( Gamma: x^2+y^2-frac{15}{4}y-1 = 0 ) e ( x^2+y^2+frac{23}{11}x-frac{47}{11}y+frac{12}{11}=0 ) sono secanti e se ne trovino i punti d'intersezione.

Prima di tutto determiniamo i centri e i raggi delle due circonferenze, usando le formule

( CBig(-frac{alpha}{2},-frac{\beta}{2} Big),,,, r = \sqrt{frac{alpha^2+\beta^2}{4}-gamma} )

( OBig(0, frac{15}{8} Big),,,, r_Gamma = \sqrt{frac{225}{64}+1} = frac{17}{8} approx 2.125 )

( O'Big( -frac{23}{22},frac{47}{22} Big) ,,,, r_{Gamma'} = \sqrt{frac{529}{484}+frac{2209}{484}-frac{12}{11}} = frac{\sqrt{1105}}{11\sqrt{2}} approx 2.137 )

Troviamo adesso la distanza tra i centri:

( OO' = \sqrt{Big(frac{23}{22} Big)^2+Big( frac{15}{8}-frac{47}{22}Big)^2} = frac{22\sqrt{17}}{88} approx 1.077 )

Se le circonferenze fossero secanti, in virtù della definizione 3 dovrebbe essere vero che ( |r_{Gamma} - r_{Gamma'}| lt OO' lt r_{Gamma}+r_{Gamma'} ). Nel nostro caso le disequazioni scritte diventano

( 0.012 = |2.125-2.137| lt 1.077 lt 2.125 + 2.137 = 4.262 )

che sono verificate: dunque le circonferenze sono effettivamente secanti.

Per trovarne i punti d'intersezione applichiamo il metodo risolutivo. Risolviamo il sistema

( \begin{cases} x^2+y^2-frac{15}{4}y-1 = 0 \ x^2+y^2+frac{23}{11}x-frac{47}{11}y+frac{12}{11} = 0 end{cases} Rightarrow \begin{cases} x^2+y^2-frac{15}{4} -1 = 0 \ frac{23}{44}y - frac{23}{11}x -frac{23}{11} end{cases} )

( \begin{cases} x^2+y^2-frac{15}{4}y-1=0 \ y-4x-4=0 end{cases} Rightarrow \begin{cases} y = 4x - 4 \ x^2+(4x+4)^2-frac{15}{4}(4x+4)-1=0 end{cases} )

( \begin{cases} y=4x-4 \ x^2+x = 0end{cases} Rightarrow \begin{cases} y=4&,&y = 0 \ x=0&,&x = -1 end{cases} )

Col che i punti d'intersezione sono ?(0,4) e ?(−1,0).

Osservazione 4: Poiché il problema proposto nell'esempio 1 ci chiedeva anche di trovare i punti d'intersezione, non sarebbe stato realmente necessario dimostrare prima che ( Gamma ) e ( Gamma' ) erano secanti. Infatti, esistendo due punti d'intersezione differenti, in base alle definizioni date le circonferenze potevano essere solo secanti. Ciò non sarebbe stato vero se per esempio avessimo trovato un solo punto d'intersezione: in questo caso non avremmo saputo distinguere tra i casi di circonferenze tangenti internamente ed esternamente.