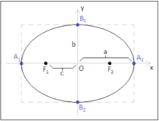
Intersezioni tra una retta e unellisse
Esempio 1: Trovare le tangenti all'ellisse di equazione [math] 9x^2+y^2-18x-10y=-25 [/math]
condotte dai punti [math] \displaystyle A(4, 5), B\Big(\frac{3}{2}, 5-\frac{3\sqrt{3}}{2}\Big) [/math]
e [math] \displaystyle C(1, 6) [/math]
.
Per risolvere questo problema seguiremo lo stesso procedimento per ciascun punto, ma otterremo tre risultati diversi. Ciò è dovuto al fatto che i tre punti si trovano in posizioni differenti del piano rispetto all'ellisse: il punto A esterno, B è interno e C appartiene all'ellisse stessa.
Il procedimento il seguente: dopo aver considerato il fascio proprio di rette centrato nel punto desiderato, intersecheremo la generica retta del
fascio con l'ellisse e porremo uguale a zero il
discriminante della risolvente. In tal modo, avendo imposto la condizione di tangenza, troveremo solo quei valori di x corrispondenti alle eventuali rette tangenti.
Il fascio proprio di rette passante per il punto A ha equazione
[math] \displaystyle \Phi_A: y = 5 + m(x-4) [/math]
Intersecando tale equazione con l'equazione dell'ellisse e ponendo
[math] \displaystyle \delta = 0 [/math]
nella risolvente,
[math] \displaystyle \begin{cases} \Phi_A \\ E \end{cases} \rightarrow \begin{cases} y=5+m(x-4) \\ 9x^2+y^2-18x-10y+25=0 \end{cases} [/math]
[math] \displaystyle 9x^2+25+m^2(x^2+16-8x)+10m(x-4) [/math]
[math]-18x-50-10mx+40m+25=0 [/math]
[math] \displaystyle (9+m^2)x^2-2(9+4m^2)x+16m^2=0 [/math]
[math] \displaystyle \delta=0 \rightarrow (9+4m^2)^2-16m^2(9+m^2)=0 \rightarrow 81-72m^2=0 [/math]
[math] \displaystyle m^2=\frac{81}{72} = \frac{9}{8} \rightarrow m=\pm\frac{3}{2\sqrt{2}} [/math]
Questa serie di calcoli ci rende due valori di x cui corrispondono le rette del fascio
[math] \displaystyle y=5\pm\frac{3}{2\sqrt{2}}(x-4) [/math]
le quali sono le due tangenti all'ellisse ? condotte dal punto ?; il fatto che ce ne siano due conferma quanto dicevamo riguardo la posizione di ? rispetto a ?.
Ripetendo lo stesso procedimento per il punto ? otterremo invece, dopo calcoli simili,
[math] \displaystyle \Phi_B: y=5-\frac{3\sqrt{3}}{2}+m\Big(x-\frac{3}{2}\Big) [/math]
[math] \displaystyle (m^2+9)x^2-3(m^2+\sqrt{3}m+6)x+\frac{9}{2}\Big(\frac{m^2}{2}+\sqrt{3}m+\frac{3}{2}\Big) = 0 [/math]
[math] \displaystyle \delta = 0 \rightarrow 27(m^2-2\sqrt{3}m+3)=0 \rightarrow m=\sqrt{3} [/math]
e dunque esiste una sola tangente ad ? condotta da ?, il che conferma il fatto che ? effettivamente appartiene all'ellisse: essa è la retta di equazione .
Provando ancora lo stesso procedimento per il punto ?, otterremo invece
[math] \displaystyle \Phi_C: y=6+m(x-1) [/math]
[math] \displaystyle (9+m^2)x^2+2(-m^2+m-9)x+(m^2-2m+1)=0 [/math]
[math] \displaystyle \delta=m^2+8 \gt 0 [/math]
Non potendo porsi
[math] \displaystyle \delta = 0 [/math]
, non è possibile che esista una retta tangente all'ellisse passante per ?: ciò è chiaro segnale che tale punto è contenuto all'interno dell'ellisse, e quindi ogni retta che lo attraversi interseca l'ellisse in esattamente due punti.
Esempio 2: Verificare che la retta [math] \displaystyle r:y=\frac{x}{3}-1 [/math]
secante all'ellisse di equazione [math] \displaystyle E: x^2+4y^2 [/math]
, e determinarne i punti d'intersezione.
Per risolvere questo genere di problema non occorre far altro che intersecare ? ed ?:
[math] \displaystyle \begin{cases}y=\frac{x}{3}-1 \\ x^2+4y^2=16 \end{cases} \rightarrow\begin{cases}y=\frac{x}{3}-1 \\ \frac{13x^2}{9}-\frac{8x}{3}-12=0 \end{cases} \rightarrow [/math]
[math] \displaystyle \rightarrow \begin{cases} x=\frac{6}{13}(2\pm\sqrt{43}) \\ y=\frac{1}{13}(-9\pm2\sqrt{43}) \end{cases} [/math]
Ci prova che i punti
[math] \displaystyle A\Big(\frac{6}{13}(2+\sqrt{43}), \frac{1}{13}(2\sqrt{43}-9) \Big) [/math]
e
[math] \displaystyle B\Big(\frac{6}{13}(2-\sqrt{43}), \frac{-1}{13}(2\sqrt{43}+9) \Big) [/math]
costituiscono l'intersezione della retta e dell'ellisse; siccome esse si intersecano in due punti, deduciamo che la retta ? è secante all'ellisse ?.
Intersezioni tra due ellissi
Esempio 3: Determinare i punti d'intersezione delle due ellissi di equazioni [math] \displaystyle E_1: 4x^2+9y^2-16x-18y-11=0 [/math]
e [math] \displaystyle E_2: 4x^2+y^2-32x-2y+61=0 [/math]
.
Per risolvere questo esercizio dobbiamo solo risolvere un sistema, così come nell'esempio 2; qui c'è la difficoltà aggiuntiva che il sistema di quarto grado, e dunque la sua risolvente sarà in generale un polinomio di quarto grado, per il quale non conosciamo una formula risolutiva semplice se non in casi molto speciali. Poniamo dunque
[math] \displaystyle \begin{cases} 4x^2+9y^2-16x-18y-11=0 \\ 4x^2+y^2-32x-2y+61=0 \end{cases} [/math]
Il primo passaggio da fare consiste nel moltiplicare entrambe le equazioni per i reciproci dei coefficienti di
[math] y^2 [/math]
, in modo tale che le equazioni risultanti presentino coefficiente pari a 1 per quel monomio:
[math] \displaystyle \begin{cases} \frac{4x^2}{9}+y^2-\frac{16}{9}-2y-\frac{11}{9}=0 \\ 4x^2+y^2-32x-2y+61=0 \end{cases} [/math]
Nella seconda equazione non è stato necessario modificare nulla poiché 1 coincide con il suo reciproco. Sottraiamo adesso le due equazioni membro a membro, e sostituiamo il risultato a una delle due equazioni, per esempio alla seconda:
[math] \displaystyle \begin{cases} \Big(4-\frac{4}{9} \Big)x^2+\Big(\frac{16}{9}-32\Big)x+\Big(61+\frac{11}{9}\Big)=0 \\ 4x^2+9y^2-16x-18y-11=0 \end{cases} \rightarrow [/math]
[math] \displaystyle \rightarrow \begin{cases} 2x^2-17x+35=0 \\ 4x^2+9y^2-16x-18y-11=0 \end{cases} [/math]
Notiamo che abbiamo del tutto eliminato ? da un'equazione; essa può allora essere risolta per ?, il che ciò consente di ottenere i valori seguenti:
[math] \displaystyle x_1=\frac{7}{2} \, \, \, \, , \, \, \, \, \, x_2=5 [/math]
Se adesso andiamo a sostituire uno alla volta i due valori ottenuti per ? nella seconda equazione e la risolviamo rispetto a ?, otteniamo il risultato cercato:
[math] \displaystyle y^2-2y-2=0 \rightarrow y=1\pm\sqrt{3} [/math]
[math] \displaystyle y^2-2y+1=0 \rightarrow y=1 [/math]
In tal modo abbiamo provato che esistono tre punti di intersezione tra le due ellissi date: essi sono
[math] \displaystyle A\Big(\frac{7}{2}, 1-\sqrt{3}\Big), B\Big(\frac{7}{2}, 1+\sqrt{3}\Big) [/math]
e
[math] \displaystyle C(5, 1) [/math]
.
Osservazione 1: Il caso analizzato nell'esempio 3, nel quale siamo giunti rapidamente alla soluzione, era in realtà molto speciale; rappresentando graficamente le ellissi ci saremmo infatti accorti che il centro della seconda giace sul semiasse maggiore della prima, il che genera particolari simmetrie che rendono il sistema facile da risolvere. Infatti, in linea di principio, quando abbiamo sottratto le due equazioni membro a membro sarebbe dovuto sparire solo il termine
[math] y^2 [/math]
. La sparizione aggiuntiva del termine ?, dovuta alla particolare disposizione delle curve, ci ha consentito di trovare velocemente la soluzione del sistema.
Altro materiale di supporto
Videolezioni di esercizi di geometria analitica