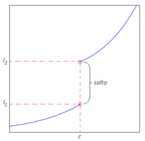
Definizione di discontinuità di terza specie
Definizione 1: Discontinuità di terza specie o eliminabile.
Sia
[math]f(x)[/math]
una funzione di dominio
[math]D \in \mathbb{R}[/math]
discontinua in
[math]c[/math]
. Tale punto
[math]c[/math]
si dice essere una discontinuit di terza specie o, il che lo stesso, una discontinuit eliminabile per
[math]f(x)[/math]
, qualora i due limiti destro e sinistro della funzione nel punto esistono, sono finiti e coincidenti, ma
[math]f(c)[/math]
è diverso dal valore del limite o non esiste.
[math] \displaystyle \lim_{x \rightarrow c^{-}} f(x) = \lim_{x \rightarrow c^{+}} f(x) = l [/math]
[math] f(c) \ne l \vee c \notin D [/math]
Definizione 2: Prolungamento per continuità.
Sia
[math]f(x)[/math]
una funzione dotata di una discontinuità eliminabile in
[math]c[/math]
.
Si dice prolungamento per continuità di
[math]f(x)[/math]
nel punto
[math]c[/math]
la funzione
[math]f_1(x)[/math]
così definita:
[math] f_1(x) = \begin{cases} f(x) & \mbox{se } x \ne c \\ l & \mbox{se } x = c \end{cases} [/math]

Osservazione 1: Il caso
[math]f(c) = l[/math]
escluso dalla definizione 1 perch se i due limiti fossero uguali e per giunta coincidessero con il valore della funzione nel punto, allora
[math]f(x)[/math]
sarebbe una funzione continua in c, contro la richiesta iniziale di discontinuità della definizione 1.
Osservazione 2: Questo tipo di discontinuità è anche detto eliminabile perché esso può essere appunto rimosso dalla funzione semplicemente ridefinendola nel punto
[math]c[/math]
nel modo
[math]f(c) = l[/math]
, cioé sostituendo la
[math]f(x)[/math]
con il suo prolungamento per continuità. facile rendersi conto, usando l'osservazione 1, che
[math]f_1(x)[/math]
continua in
[math]c[/math]
; essa si distingue dalla funzione iniziale
[math]f(x)[/math]
solo per il valore che assume nel punto
[math]c[/math]
. Si noti che una simile procedura di eliminazione della discontinuità è invece impossibile nel caso delle discontinuità di
prima e
seconda specie, poiché i limiti destro e sinistro della funzione in c non sono uguali e finiti e dunque c non è ben definito.
Esempi di funzioni con discontinuità di terza specie
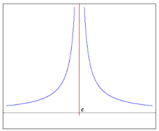
Esempio 1: La funzione non definita nel punto
[math]c[/math]
.
Consideriamo la funzione
[math]y = \frac{\sin x}{x}[/math]
, il cui grafico rappresentato nella figura a sinistra.

Dal momento che la
[math]x[/math]
appare al denominatore, il punto
[math]c = 0[/math]
non appartiene al dominio
[math]D[/math]
della funzione, che infatti proprio
[math]D = \mathbb{R} - {0}[/math]
; ciò significa che
[math]f(0)[/math]
non esiste. Secondo la definizione 1, per verificare che
[math]c = 0[/math]
sia una discontinuità di terza specie ci basta dunque solo far vedere che i due limiti esistono, sono finiti e coincidenti:
[math] \displaystyle \lim_{x \rightarrow 0^{-}} \frac{sin x}{x} = 1 = \lim_{x \rightarrow 0^{+}} \frac{sin x}{x} [/math]
I limiti in questione si risolvono subito grazie alla conoscenza pregressa del limite notevole
[math] \displaystyle \lim_{x \rightarrow 0} \frac{\sin x}{x} = 1 [/math]
Per questo motivo la funzione esaminata ha effettivamente una discontinuità eliminabile in
[math]c=0[/math]
, e quindi se ne può considerare il prolungamento per continuità. Esso è raffigurato nel grafico a destra, e la sua equazione, in virtù della definizione 2, è
[math] f_1(x) = \begin{cases}\frac{\sin x}{x} & \mbox{se } x \ne 0 \\ 1 & \mbox{se } x = 0 \end{cases} [/math]
Osservazione 3: Il caso esaminato nell'esempio 1 si verifica anche per le funzioni
[math] \frac{e^x – 1}{x} \mbox{, } \frac{1-\cos x}{x^2} \mbox{, } \frac{1 – \cos x}{x} \mbox{, } \ldots [/math]
ovvero per tutti quei limiti notevoli che si presentano inizialmente nella forma
[math]\frac{0}{0}[/math]
ma si riconducono poi a un risultato finito. Dal momento, infatti, che i limiti considerati esistono finiti, allora i limiti destro e sinistro delle suddette funzioni in
[math]c = 0[/math]
esistono anchessi, e per di più sono finiti e coincidenti. Inoltre è chiaro che in questi casi si ha sempre
[math]c \notin D[/math]
, visto che si presentano nella forma indeterminata
[math]\frac{0}{0}[/math]
.
Esempio 2: La funzione definita nel punto
[math]c[/math]
.
Si prenda adesso in considerazione una funzione
[math]f(x) il cui valore sia sempre nullo per ogni numero reale, ad esclusione dei
numeri interi, sui quali la funzione assume il valore 1:
[math] f(x) = \begin{cases}1 & \mbox{se } x \in \mathbb{Z} \\ 0 & \mbox{se } x \in \mathbb{R} – \mathbb{Z} \end{cases} [/math]
Il grafico di
[math]f(x)[/math]
è rappresentato di seguito. Vogliamo far vedere che la funzione in esame è dotata di una quantità infinita di discontinuità di terza specie, esattamente coincidenti con i
numeri interi. Sia dunque
[math]n \in \mathbb{Z}[/math]
; poiché in questo caso il dominio della funzione è
[math]D = \mathbb{R}[/math]
, il valore
[math]f(n)[/math]
esiste e, stando alla definizione di
[math]f(x)[/math]
, risulta
[math]f(n) = 1[/math]
. Calcoliamo adesso i limiti destro e sinistro di
[math]f(x)[/math]
per
[math]x \rightarrow n[/math]
:
[math] \displaystyle \lim_{x \rightarrow n^{-}} f(x) = 0 = \lim_{x \rightarrow n^{+}} f(x) R\rightarrow l = 0 [/math]
Tali limiti sono entrambi uguali a 0 perché, dal momento che la distanza tra due numeri interi consecutivi è sempre uguale a 1, è possibile prendere una successione di punti reali convergente a
[math]n[/math]
tutta costituita da numeri compresi nell'insieme
[math](n-1, n) \cup (n, n+1)[/math]
, sui quali è certamente
[math]f(x) = 0[/math]
. Perciò i limiti destro e sinistro di
[math]f(x)[/math]
in
[math]n[/math]
esistono, sono finiti, coincidenti tra loro e distinti dal numero
[math]f(n)[/math]
. Ci prova che ogni
[math]n \in \mathbb{Z}[/math]
è una discontinuità di terza specie per la nostra funzione
[math]f(x)[/math]
.
[img]https://www.skuola.net/news_foto/2015/10/grafico-funzione-discontinuita-terza-specie-z-q[/img]
Questo ci consente di considerarne il prolungamento per continuità, che secondo quanto affermato dalla definizione 2
[math] f_1(x) = \begin{cases} l & \mbox{se } x \in \mathbb{Z} \\ 0 & \mbox{se } x \in \mathbb{R} – \mathbb{Z} \end{cases} [/math]
Dal momento per che in questo caso risulta
[math]l = 0[/math]
, il prolungamento per continuità di
[math]f(x)[/math]
è la funzione nulla su tutti i
numeri reali, ovvero
[math]f(x) = 0[/math]
.