Archi e angoli al centro
Tra gli archi e gli angoli al centro di una circonferenza esiste una corrispondenza biunivoca, infatti, ad ogni angolo al centro corrisponde un determinato arco, e viceversa.Alcuni concetti che abbiamo visto per gli angoli possono quindi essere estesi agli archi.
Teorema: Due archi non nulli congruenti hanno lo stesso raggio.
Quindi, possiamo affermare che due archi possono essere congruenti se sono contenuti nella stessa circonferenza, o in circonferenza congruenti; mentre, due archi appartenenti a circonferenze non congruenti, non possono essere congruenti.
Teorema: Due archi aventi lo stesso raggio sono congruenti se e solo se sono congruenti i corrispondenti angoli al centro.
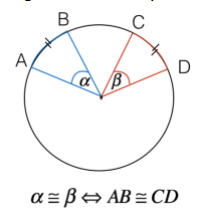
Questo concetto può essere ampliato anche al caso dei settori circolari: due settori circolari aventi lo stesso raggio sono congruenti se e solo se sono congruenti i corrispondenti angoli al centro.
Una conseguenza immediata del precedente teorema, è che la bisettrice di un angolo al centro divide l'arco corrispondente in due parti congruenti.
Allo stesso modo, una semiretta che ha origine al centro di una circonferenza e passa per il punto medio di un arco è bisettrice dell'angolo al centro corrispondente.
Proprietà delle corde
Cominciamo ad esaminare le proprietà delle corde, considerando il diametro della circonferenza, che, come sappiamo, è una corda passante per il centro della circonferenza, e la sua lunghezza è pari a due volte il raggio.Teorema: Un diametro è maggiore di qualunque corda della stessa circonferenza non passante per il centro.
Non vi è una corrispondenza biunivoca tra corde e angoli al centro di una stessa circonferenza; tuttavia, vi sono delle relazioni di congruenza tra corde e archi (o angoli al centro) corrispondenti.
Teorema: In una stessa circonferenza, o in circonferenze congruenti, ad angoli al centro congruenti corrispondono corde congruenti e ad archi congruenti corrispondono corde congruenti.

Il teorema precedente può anche essere espresso in questo modo:
In una stessa circonferenza, o in circonferenza congruenti, a corde congruenti minori del diametro corrispondono archi minori della semicirconferenza congruenti tra loro, e angoli al centro convessi congruenti tra loro.
Vediamo ora altre importanti proprietà delle corde, che seguono dal fatto che, congiungendo gli estremi di una corda con il centro della circonferenza, si ottiene un triangolo isoscele che ha per lato il raggio della circonferenza, e per base la corda stessa:
- l'asse di una corda passa per il centro della circonferenza e biseca gli angoli al centro e gli archi ad essa corrispondenti;
- la retta passante per il centro della circonferenza e perpendicolare ad una corda biseca la corda, gli angoli al centro e gli archi ad essa corrispondenti;
- la retta passante per il centro della circonferenza e per il punto medio della corda è perpendicolare alla corda e biseca gli angoli al centro e gli archi ad essa corrispondenti;
- la bisettrice di un angolo al centro biseca la corda ad essa corrispondente, e le è perpendicolare.
Teorema: Date in una stessa circonferenza, o in circonferenza congruenti, due corde non congruenti, la maggiore ha distanza minore dal centro e, viceversa, quella che ha distanza maggiore è la minore.