Parallelogrammi e altri quadrilateri

In questo appunto di geometria euclidea del piano è riportata una descrizione molto esaustiva sui quadrilateri. Il contenuto riguarda le definizioni e le proprietà di questa classe di poligoni, i principali teoremi per stabilire le condizioni sufficienti a verificare un parallelogramma e le sue proprietà, si prosegue con il rettangolo, il quadrato e rombo che sono particolari parallelogrammi. Un paragrafo conclusivo è dedicato ai trapezi che sono un’altra classe di quadrilateri.

Quadrilateri- Definizioni e proprietà

Un quadrilatero è un poligono con quattro lati, quattro vertici e quattro angoli.
Un parallelogramma è un quadrilatero avente i lati opposti paralleli.
In un quadrilatero, i lati opposti sono i lati non consecutivi, in figura sono opposti i lati AD e BC e i lati AB e DC che sono paralleli a due a due.
Gli angoli opposti sono gli angoli i cui vertici non sono gli estremi di uno stesso lato. Sempre in figura sono opposti gli angoli A con C e B con D.

In ogni quadrilatero, e quindi anche nel parallelogramma, la somma degli angoli interni è di 360°; è, quindi, equivalente a due angoli piatti.
Il numero delle diagonali che si possono tracciare è dato dal prodotto tra il numero dei lati e il numero dei lati meno 3, il tutto diviso 2, in simboli matematici:

se

abbiamo proprio .
La somma degli angoli esterni di un quadrilatero come di ogni poligono, non dipende dal numero dei lati ed è sempre pari ad un angolo giro.
I quadrilateri sono classificati in quattro gruppi: scaleni, deltoidi, trapezi e parallelogrammi.

Proprietà dei parallelogrammi

In ogni parallelogramma:

• i lati opposti sono congruenti;
• gli angoli opposti sono congruenti;
• gli angoli adiacenti a ciascun lato sono supplementari;
• le diagonali hanno lo stesso punto medio ( le diagonali si tagliano scambievolmente a metà ), che viene detto centro del parallelogramma.

Queste proprietà sono condizioni necessarie affinché un quadrilatero sia un parallelogramma.

Criteri per stabilire se un quadrilatero è un parallelogramma

Vediamo ora dei teoremi che ci illustrano quali sono le condizioni sufficienti che ci permettono di stabilire se un quadrilatero è un parallelogramma. Riportiamo di seguito cinque teoremi

Teorema 1: Un quadrilatero avente i lati opposti congruenti è un parallelogramma.

Teorema 2: Un quadrilatero avente gli angoli opposti congruenti è un parallelogramma.

Teorema 3: Un quadrilatero avente gli angoli adiacenti a ciascun lato supplementari è un parallelogramma.

Teorema 4: Un quadrilatero avente le diagonali con lo stesso punto medio è un parallelogramma.

Teorema 5: Un quadrilatero avente una coppia di lati opposti sia paralleli che congruenti è un parallelogramma.

Di conseguenza, qualora trovassimo nelle ipotesi di un problema una delle condizioni precedentemente elencate, potremmo concludere che la figura in questione è proprio un parallelogramma. Una volta dimostrato che si tratta di un parallelogramma possiamo sfruttarne tutte le proprietà. In un parallelogramma, si definisce altezza, rispetto ad un lato assunto come base, la distanza tra il lato opposto alla base e la base stessa, ci sono perciò due altezze.

Rettangoli e loro proprietà

Un rettangolo è un parallelogramma avente i quattro angoli retti. Questo poligono gode di tutte le proprietà dei parallelogrammi, in particolare le sue diagonali sono congruenti e ciò si può facilmente dimostrare con il primo criterio di congruenza dei triangoli. Facendo riferimento alla figura sotto, consideriamo i due triangoli rettangoli ABC e ABD che si formano tracciando le diagonali AC e BD. Essi hanno:

• il lato AB in comune;
• i lati AD e BC congruenti perché il rettangolo è un parallelogramma e ha i lati opposti congruenti;
• gli angoli in A e in B congruenti perché entrambi retti;

Per il primo criterio di congruenza i triangoli ABC e ABD sono dunque congruenti, in particolare AC è congruente a BD, come volevasi dimostrare. Ricordiamo infine che la diagonale è l’ipotenusa del triangolo rettangolo avente come cateti i lati, perciò ogni diagonale è sempre maggiore di ciascun lato.

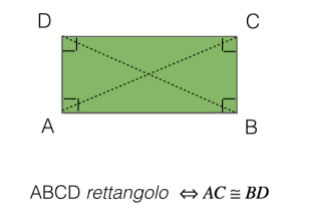
Per poter affermare che un parallelogramma è un rettangolo ci basta sapere che solo un suo angolo è retto, e possiamo concludere che lo sono anche gli altri tre, due perché supplementari del primo, l'altro perché opposto al primo.

Rombo - Parallelogramma con lati congruenti

Il rombo è un particolare parallelogramma caratterizzato dall’avere i quattro lati congruenti. Le diagonali si dividono a metà ma sono di lunghezza diversa, sono identificate some diagonale maggiore D e diagonale minore. In riferimento alla figura sopra, la diagonale maggiore unisce i vertici A e C, la minore unisce i vertici B e D. Le diagonali di un rombo sono anche bisettrici degli angoli interni.
Per il rombo vale dunque il seguente teorema: in un rombo le diagonali sono perpendicolari fra loro e sono bisettrici degli angoli interni.

Dimostrazione

ABCD è un parallelogramma, e in quanto tale le sue diagonali si tagliano scambievolmente a metà. La diagonale BD divide il rombo in due triangoli isosceli perché i quattro lati del rombo sono tutti congruenti. Detto M il punto medio di BD, nei due triangoli isosceli ABD e DCB, i segmenti AM e CM sono mediane relative alla base comune BD ma anche altezze e bisettrici relativamente allo stesso lato. Da ciò deriva che:

e AC è bisettrice di

Allo stesso modo si procede con l’altra diagonale AC, considerando i triangoli isosceli ABC e ADC sulla base comune AC. Si ottiene ancora che:

e che BD è bisettrice di

Il teorema inverso del recedente afferma che: Un parallelogramma è un rombo se:

• le diagonali sono perpendicolari, oppure
• un suo angolo ha per bisettrice la diagonale passante per il suo vertice.

Quadrato - sia rettangolo che rombo

Un quadrato è un parallelogramma in cui tutti gli angoli sono retti e tutti i lati sono uguali. Per definizione il quadrato è allora sia un rettangolo sia un rombo, quindi per esso valgono tutte le proprietà del rettangolo e del rombo relative alle diagonali. Il quadrato è perciò un quadrilatero equilatero ed equiangolo, i suoi lati sono tutti congruenti e i suoi angoli sono tutti retti. Per dimostrare che un parallelogramma è un quadrato bisogna far vedere che è sia un rettangolo che un rombo.

Per il quadrato si dimostra infatti il seguente Teorema:
Le diagonali di un quadrato sono congruenti, perpendicolari tra loro e bisettrici degli angoli.
Il teorema inverso afferma che: Un parallelogramma è un quadrato se in esso le diagonali sono congruenti e perpendicolari, oppure se le diagonali sono congruenti e un angolo è diviso per metà dalla diagonale che passa per il suo vertice.

Trapezi non sono parallelogrammi

Un trapezio è un quadrilatero avente solo due lati opposti paralleli.
I due lati paralleli si chiamano basi del trapezio, e in particolare base maggiore B il lato più lungo, base minore b quello più corto; gli altri si dicono lati obliqui. Si definisce altezza h la distanza tra le due basi.
Se i lati obliqui sono congruenti, il trapezio si definisce isoscele; se uno dei due lati obliqui è perpendicolare alla base, il trapezio viene detto rettangolo, se i suoi 4 lati sono tutti diversi allora è detto scaleno.
Nei trapezi gli angoli adiacenti ad un lato obliquo sono supplementari perché sono coniugati interni fra le rette delle due basi parallele, e la trasversale su cui giace il lato obliquo.
Riportiamo i teoremi che dimostrano le proprietà del trapezio isoscele.
Teorema: In un trapezio isoscele gli angoli adiacenti a ciascuna base sono congruenti.
Teorema: In un trapezio isoscele le diagonali sono congruenti.
Sono condizioni sufficienti, affinché un trapezio sia isoscele, gli inversi dei teoremi sopra citati

Altro materiale di supporto sui parallelogrammi