_stan
di _stan
(320 punti)
6' di lettura
In questo appunto vengono descritte in modo approfondito le disequazioni goniometriche sia elementari che complesse, vengono inoltre proposti i metodi risolutivi algebrici e grafici e vengono riportati alcuni esempi.

Disequazioni goniometriche elementari

Le disequazioni goniometriche elementari si presentano con una funzione goniometrica posta maggiore, minore, maggiore o uguale, minore o uguale a un numero reale; le disequazioni goniometriche elementari, quindi, possono essere di questi tipi:
[math]sin x \gt m,,,, (sin x \ge m) ,,,, , ,,,, \sin x \lt m ,,,,, (\sin x \le m)[/math]

[math]cos x \gt m,,,, (cos x \ge m) ,,,, , ,,,, cos x \lt m ,,,,, (cos x \le m)[/math]

[math]tan x \gt m,,,, (tan x \ge m) ,,,, , ,,,, tan x \lt m ,,,,, (tan x \le m)[/math]

[math]cot x \gt m,,,,, (cot x \ge m) ,,,, , ,,,, cot x \lt m ,,,,,, (cot x \le m)[/math]

In alcuni casi, queste disequazioni possono essere risolte immediatamente; infatti, considerando che il seno e il coseno di un angolo sono sempre compresi tra -1 e 1, possiamo affermare che:

  • le disequazioni del tipo (sin x sempre soddisfatte;
  • le disequazioni del tipo (sin x non sono mai soddisfatte.
Negli altri casi, possiamo risolvere le disequazioni facendo riferimento alla circonferenza goniometrica, e studiando le varie parti della circonferenza che vengono individuate dall'angolo in questione.

Esempio:
Risolviamo la seguente disequazione elementare:

[math]sin x \gt -\frac{1}{2}[/math]

Sappiamo che (

[math]sin x[/math]
) è l'ordinata dell'estremo dell'arco corrispondente all'angolo di ampiezza
[math]x[/math]
, sulla circonferenza goniometrica; risolvere la disequazione significa determinare tutti gli archi aventi ordinata maggiore di
[math]-1/2[/math]
.

Per prima cosa, consideriamo l'equazione associata (

[math]sin x = -\frac{1}{2}[/math]
); sappiamo che essa ha per soluzioni:
[math]x = \frac{7}{6} \pi + 2k \pi ,,,, , ,,,, x=-\frac{\pi}{6}+2k \pi,,,, (k in \mathbb{Z})[/math]

Le soluzioni della disequazione sono date da tutti i punti, sulla circonferenza goniometriche, che hanno ordinata maggiore delle ordinate dei punti P e Q; tali punti si trovano, quindi, al di sopra di questi punti, e gli angoli che li individuano appartengono al seguente intervallo, che costituisce le soluzioni della disequazione:Intervallo soluzioni disequazione goniometrica per via grafica: sen x > -1/2

[math]-\frac{\pi}{6} + 2k \pi \lt x \lt \frac{7}{6} \pi + 2k \pi ,,,, , ,,,, (k in \mathbb{Z})[/math]

Per ulteriori approfondimenti sulle funzioni goniometriche e sulle loro proprietà vedi anche qua

Disequazioni riconducibili a disequazioni elementari

Alcune disequazioni possono presentarsi in una forma più complessa, ma possono essere ricondotte, mediante raccoglimenti a fattore comune, o altre scomposizioni, a disequazioni elementari.

Vediamo un esempio:
Consideriamo la seguente disequazione:

[math]2cos^2 x + cos x - 1 \lt 0[/math]

Risolviamo, per prima cosa, l'equazione associata, e individuiamo i valori di (cos x) che soddisfano l'equazione:

[math]2cos^2 x + cos x - 1 = 0 \rightarrow cos x = \frac{-1 \pm \sqrt{1+8}}{4} = \frac{-1 \pm 3}{4}[/math]

[math]cos x = \frac{-1+3}{4} = \frac{2}{4} = \frac{1}{2} \vee cos x = \frac{-1-3}{4} = \frac{-4}{4} = -1[/math]

Poiché la disequazione è maggiore di zero, essa è soddisfatta per valori esterni all'intervallo delle radici:

[math]cos x \lt -1 \vee cos x \gt \frac{1}{2}[/math]

Ora, sappiamo che

[math]cos x \lt -1[/math]
è impossibile, quindi le soluzioni della disequazione sono date solo dalla seconda disequazione, che è una disequazione elementare; rappresentiamo la situazione sulla circonferenza goniometrica:

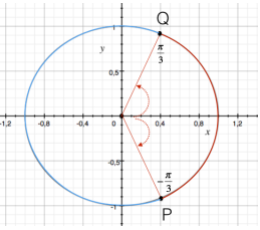
Disequazioni goniometriche: soluzione grafica
Notiamo che il coseno assume il valore

[math]1/2[/math]
negli angoli
[math]\frac{\pi}{3}[/math]
e
[math]-\frac{\pi}{3}[/math]
; gli angoli che soddisfano la disequazione sono quelli che individuano punti sulla circonferenza che hanno ascissa maggiore di
[math]1/2[/math]
; le soluzioni della disequazione sono, quindi, date dal seguente intervallo:
[math]-\frac{\pi}{3} + 2k \pi \lt x \lt \frac{\pi}{3} + 2k \pi[/math]

Disequazioni lineari in seno e coseno

Le disequazioni lineari in seno e coseno si presentano in questa forma:
[math]a sin x + b cos x + c \gt 0 ,,,,, , ,,,,, a sin x + b cos x + c \lt 0[/math]

[math]a sin x + b cos x + c \ge 0 ,,,,, , ,,,,, a sin x + b cos x + c \le 0[/math]

Possiamo risolvere questo tipo di equazioni in diversi modi; consideriamo, per il momento, la disequazione con il simbolo >; i ragionamenti fatti si possono applicare anche agli altri casi.

Risoluzione con il metodo grafico
Così come per le equazioni lineari, anche in questo caso si pone (sin x = Y) e (cos x = X), e si trovano le intersezioni della retta di equazione (aX + by + c = 0) con la circonferenza goniometrica.

Dopo aver determinato tali punti, si individuano i punti della circonferenza goniometrica che appartengono al semipiano (

[math]aX + by + c \gt 0[/math]
); tali punti costituiscono le soluzioni della disequazione iniziale.

Risoluzione con i metodi algebrici
Per risolvere con metodi algebrici una disequazione lineare in seno e coseno, possiamo utilizzare due diverse strategie.

  • Primo metodo: possiamo utilizzare le formule parametriche razionali, trasformando la disequazione in seno e coseno in una disequazione in (
    [math]t = tan \frac{x}{2}[/math]
    );
  • Secondo metodo: possiamo trasformare il primo membro della disequazione nella forma:
    [math]A \cdot sin(x + \alpha) + B[/math]

    e risolvere poi la disequazione elementare che ne deriva.

Per ulteriori approfondimenti sul procedimento da seguire per risolvere una disequazione vedi anche qua

Vuoi approfondire Trigonometria – Esercizi, problemi e formule di Trigonometria con un insegnante esperto?
Trovalo su Ripetizioni.it