| 1. Problemi classici che coinvolgono i grafi
I quattro esempi "storici" proposti mettono in evidenza come problemi molto diversi tra loro possono essere modellati mediante la stessa struttura matematica: il grafo. Tra le altre applicazioni:
Nella tabella seguente alcuni esempi di situazioni problematiche concrete che possono ricnodnotte ai problemi classici:
2. Grafi : definizioni e proprietà fondamentali GRAFO NON ORIENTATO
Notiamo subito che : ADIACENZA E INCIDENZA GRADO DI UN VERTICE TEOREMA Indicando con vi un vertice di un grafo, con nv il numero di vertici e con ns il numero di spigoli, si ha MULTIGRAFO PASSEGGIATA - PERCORSO - SENTIERO - CICLO
|
In un grafo, ogni ciclo deve avere lunghezza maggiore o uguale a 3
GRAFO CONNESSO
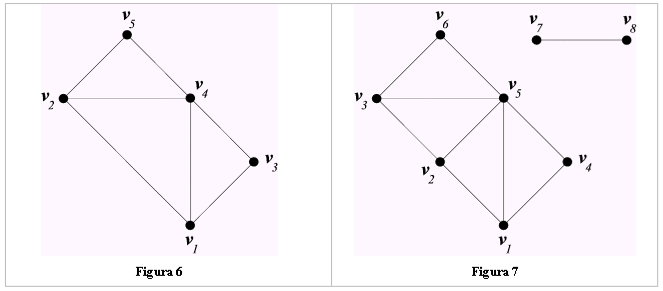
Un grafo si dice connesso (Fig.6) se esiste un sentiero tra due qualsiasi suoi vertici. In fig.7 è riportato un esempio di grafo non connesso (p.e., non esiste un sentiero da v4 a v7 ).
GRAFO TRAVERSABILE
Un grafo (o un multigrafo) si dice traversabile se può essere disegnato senza mai alzare la penna dal foglio e senza mai passare due volte per lo stesso spigolo.
In un grafo traversabile, quindi, esiste un passeggiata nella quale sono inclusi tutti i vertici e dove vengono usati tutti gli spigoli una sola volta (mentre si può passare per un vertice quante volte si vuole). Tale passeggiata si chiama percorso traversabile. Un esempio di grafo traversabile è dato in Fig. 6: (v1 , v2 , v4 , v1 , v3 , v4 , v5 ) è un percorso traversabile.
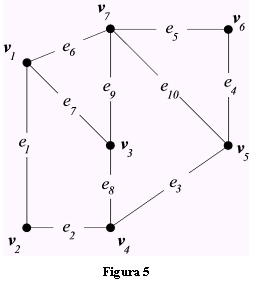
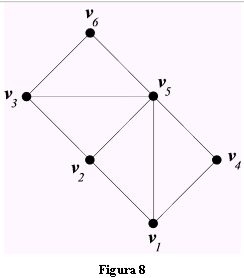
| A titolo di esempio determiniamo le caratteristiche del grafo connesso di Fig.8. Consideriamo la passeggiata da v4 a v6 : (v4, v1, v2, v5, v1, v2, v3, v6). Questa passeggiata non è un percorso, perché lo spigolo (v1, v2) viene usato due volte. La successione (v4, v1, v5, v2, v6) non è una passeggiata, perché manca lo spigolo (v2, v6). La successione (v4, v1, v5, v2, v3, v5, v6) |
|
3. Analisi del grafo dei ponti di Koenigsberg
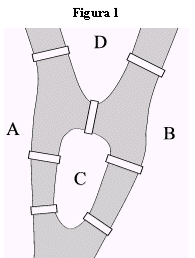
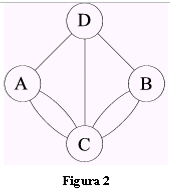
Siamo ora in grado di studiare il problema dei ponti di Koenigsberg.
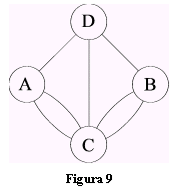
Il problema ammette soluzioni se si riesce a dimostrare che il multigrafo associato al problema (fig.9) è traversabile.
| Vediamo come ha ragionato Eulero. Consideriamo un multigrafo traversabile, e supponiamo che un percorso traversabile P non inizi (e quindi non finisca) in V. Il vertice V è sicuramente di grado pari perché ogni volta che P entra in V da uno spigolo, deve sempre uscirne da uno spigolo non usato in precedenza; in altre parole nel vertice V il numero di ingressi è uguale al numero di uscite, e quindi il grado di V è pari. Questo significa che se un vertice U ha grado dispari, allora il percorso P deve iniziare e finire in U. Di conseguenza, se un multigrafo ha più di due vertici dispari, allora non è traversabile. Il grafo fig. 9 ha quattro vertici dispari, e quindi non è traversabile: il problema dei ponti di Koenigsberg non ha soluzione. |
|
Eulero, in effetti, dimostrò la proposizione inversa a quella esposta in precedenza. In particolare dimostrò il seguente teorema.
TEOREMA DI EULERO
Un grafo connesso finito è un GRAFO traversabile se e solo se ha due vertici di valenza dispari, oppure nessuno.
4. Grafi hamiltoniani
I grafi traversabili si chiamano grafi euleriani. In questi grafi, esiste una passeggiata chiusa che comprende tutti gli spigoli del grafo una sola volta.
Il matematico William Rowland Hamilton si pose il problema duale: quali sono le condizioni affinché esista una passeggiata chiusa che includa tutti i vertici una sola volta? Tale passeggiata è evidentemente un ciclo, e prende il nome di ciclo di Hamilton. Non è ancora stato trovato un metodo generale per determinare il ciclo hamiltoniano di un grafo qualunque, e molti matematici sono attualmente impegnati nella ricerca di questo metodo.
Un interessante problema "hamiltoniano" è il problema del commesso viaggiatore, già accennato all'inizio: un commesso viaggiatore deve visitare dei clienti in alcune città. Come deve scegliere il percorso stradale che collega tutte le città da visitare con la città di partenza, in modo da minimizzare i chilometri da percorrere?
Il problema può essere modellato da un grafo, in cui i vertici sono le città (e qualche incrocio stradale…), mentre gli spigoli sono tutte le strade percorribili che collegato le città tra di loro (compresa la città di partenza)
Il lettore provi a risolvere il problema seguente, costruendo il grafo appropriato.
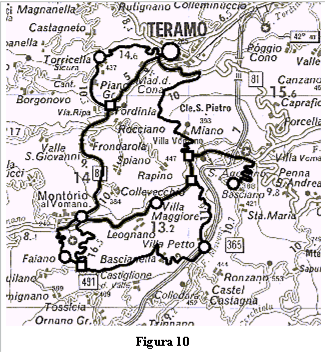
| Problema Un tecnico di manutenzione di impianti termici, residente a Teramo, deve visitare dei clienti nelle seguenti località: · Torricella Sicura · Montorio · Faiano · Villa Petto · Villa Maggiore · Castel Castagna · Basciano
Il tecnico vuole percorrere meno strada possibile. Qual è il percorso minimo? O, in altri termini, qual è il ciclo hamiltoniano del grafo associato al problema? I dati sulle lunghezze delle strade sono inseriti nella cartina. |
|
5. Grafi planari
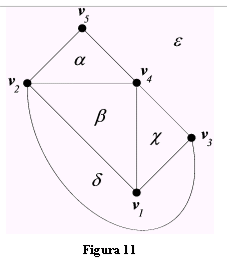
Un grafo si dice planare se può essere tracciato in un piano e se i suo spigoli non si intersecano. Chiameremo mappa un grafo planare. Una mappa divide in facce il piano che la contiene.
| Per esempio la mappa in fig. 11 è suddivisa in cinque facce TEOREMA |
|
Importante (anche nella geometria solida) è il seguente:
TEOREMA DI EULERO
Indicando con nv il numero di vertici di una mappa connessa M, con ns il numero di spigoli e con il numero delle facce, si ha: nv - ns + nF =2
6. Mappe colorate
Consideriamo una mappa M. Due facce di M si dicono adiacenti se hanno uno spigolo in comune. Una colorazione di M consiste nell'assegnare ad ogni faccia di M un colore in modo che facce adiacenti abbiano colori diversi.
Una mappa M è n-colorabile se bastano n colori. Possiamo ora esaminare il seguente teorema :
TEOREMA DEI QUATTRO COLORI
Ogni mappa è 4-colorabile
La formulazione del teorema è di una semplicità disarmante. Nonostante questo, la sua dimostrazione ha impegnato per quasi 130 anni i migliori matematici. La sua prima formulazione risale al 1852, quando l'inglese Francis Guthrie in una lettera lo propose al fratello Frederick, allievo del famoso matematico Augustus De Morgan. Del problema venne a conoscenza Hamilton, al quale De Morgan il 23 ottobre del 1852 scriveva :
"… un mio studente mi ha chiesto oggi il perché di un fatto. Egli dice che se si divide una figura, in modo qualsiasi, in regioni e si vogliono colorare queste regioni in modo diverso, cioè in modo che regioni confinanti risultino colorate in modo diverso, possono essere necessari quattro colori ma non di più: ossia ogni carta geografica può essere colorata con un massimo di 4 colori".
Il problema non interessò immediatamente né Hamilton né i matematici dell'epoca. Tuttavia, il fatto che non si riusciva a trovare una dimostrazione coinvolse via via sempre più matematici. Per 124 anni il teorema rimase una congettura fino a che, nel 1976, due matematici dell'Università dell'Illinois (USA), Kenneth Appel e Wolfgang Haken, con l'ausilio determinante dei più potenti calcolatori dell'epoca, riuscirono a dimostrare il teorema. Occorsero più di 1200 ore di tempo-macchina su tre diversi elaboratori elettronici. Era la prima volta che un teorema veniva dimostrato con l'ausilio di un elaboratore elettronico, cosa che suscitò all'epoca non poche discussioni tra i matematici.
7. Il salto del cavallo
Il matematico Dudeney inventò 80 anni fa il seguente problema, assai facile da risolvere con un grafo, ma che presenta notevoli difficoltà se risolto per tentativi.
Consideriamo la scacchiera ridotta di fig. 12, in cui ci sono 2 cavalli neri e due cavalli bianchi. Il gioco consiste nello scambiare di posto i due cavalli bianchi con i due neri.
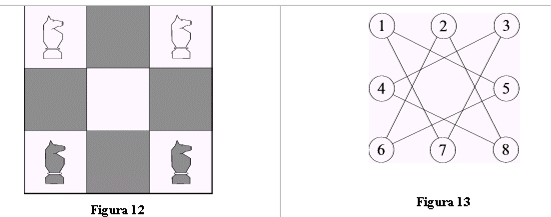
Costruito il grafo del problema (fig.13), notiamo innanzitutto che il grafo non è planare. Ma questo non è un problema: si può fare in modo di disegnare un grafo equivalente a quello di fig.13, ma senza lati che si intersecano.
Un'interessante articolo su un problema analogo a questo (con una scacchiera più grande di quella di fig.12) può essere letto alla pagina
http://space.tin.it/scuola/vdepetr/t18/Text18.htm
Giovanni Valentini



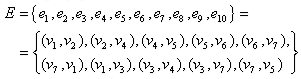
 Play
Play
 Play
Play
 Play
Play


