_stan
di _stan
(320 punti)
5' di lettura
In questi appunti troverai delle informazioni riguardanti gli integrali definiti, con un approfondimento sulla loro applicazione per il calcolo dell'area

A cosa servono gli integrali definiti nei problemi matematici

Molto spesso, nei problemi matematici, ma anche in quelli di carattere scientifico e tecnico in generale, capita di dover determinare l'area compresa tra il grafico di una funzione e l'asse delle ascisse. Gli integrali definiti ci permettono di assolvere questo compito.

Consideriamo una funzione

[math]f(x)[/math]
continua in un intervallo chiuso e limitato
[math][a;b][/math]
e ipotizziamo, per il momento, che la funzione sia positiva in tale intervallo.

Integrali: area sottesa dal grafico di una funzione
La parte di spazio compresa tra le rette

[math]x = a[/math]
,
[math]x = b[/math]
,
[math]y = f(x)[/math]
e
[math]y = 0[/math]
, viene detta area sottesa dal grafico di
[math]f(x)[/math]
nell'intervallo
[math][a;b][/math]
.

Come calcolare l'area utilizzando gli integrali definiti

Per calcolare l'area di tale regione dello spazio, procediamo in questo modo: suddividiamo l'intervallo, che ha ampiezza
[math]b-a[/math]
, in
[math]n[/math]
parti uguali, che avranno tutte lunghezza
[math] \Delta x = \frac{b-a}{n} [/math]
.

Ciascuna di queste parti rappresenta la base di un rettangolo. Distinguiamo i rettangoli che si formano in due tipi: quelli colorati hanno altezza uguale al valore minimo che la funzione assume in un determinato intervallo, mentre quelli contornati di nero hanno altezza uguale al valore massimo che la funzione assume nell'intervallo.

Approssimazione dell'area di una funzione per difetto e per eccesso

Cosa sono la somma integrale superiore e la somma integrale inferiore e come si calcolano

L'area della regione azzurra, cioè l'area di tutti i rettangoli più piccoli, è data dalla seguente somma:
[math] s_n = m_1 \cdot \Delta x + m_2 \cdot \Delta x + l\dots + m_n \cdot \Delta x = \sum_{k=1}^n (m_k \cdot \Delta x) [/math]
dove, con
[math]m[/math]
indichiamo il valore minimo che la funzione assume in un determinato intervallo.

Allo stesso modo, possiamo definire l'area di tutti i rettangoli con il bordo, cioè i rettangoli più grandi:

[math] S_n = M_1 \cdot \Delta x + M_2 \cdot \Delta x + l\dots + M_n \cdot \Delta x = \sum_{k=1}^n (M_k \cdot \Delta x) [/math]
dove, con
[math]M[/math]
indichiamo il valore massimo che la funzione assume in un determinato intervallo.

Le somme precedenti prendono il nome, rispettivamente, di somma integrale inferiore e somma integrale superiore della funzione.Possiamo notare che le somme precedenti rappresentano un'approssimazione per difetto e per eccesso della misura dell'area sottesa al grafico di

[math]f(x)[/math]
. In particolare, all'aumentare del numero
[math]n[/math]
di suddivisioni dell'intervallo
[math][a;b][/math]
, il valore delle somme migliora sempre di può, avvicinandosi dal basso, o dall'alto, al valore dell'area cercato.

Possiamo quindi dire che il valore di entrambe le somme, all'aumentare di

[math]n[/math]
, converge a un unico limite, che rappresenta la misura
[math]I[/math]
dell'area del trapezoide individuato dalla funzione.

Vale quindi, il seguente teorema: Le successioni delle somme integrali inferiori e superiori relative a una funzione

[math]f(x)[/math]
, continua in un intervallo chiuso e limitato
[math][a;b][/math]
, sono convergenti e ammettono, per
[math]n[/math]
che tende all'infinito, lo stesso limite finito:
[math] I = lim_{n \rightarrow +\infty} s_n = lim_{n \rightarrow +\infty} S_n [/math]

Il valore comune di tali somme si chiama, per definizione, integrale definito della funzione

[math]f(x)[/math]
nell'intervallo
[math][a;b][/math]
, e si indica con il simbolo:
[math] \int_a^b f(x) [/math]

Nel caso in cui la funzione sia negativa in un determinato intervallo, si può applicare lo stesso ragionamento utilizzato in precedenza. Il limite (negativo) delle somme rappresenta, in valore assoluto, la misura dell'area delimitata dall'asse delle

[math]x[/math]
e dal grafico della funzione. Tuttavia, per convenzione, si considerano negative le misure delle aree che si trovano al di sotto dell'asse delle ascisse.

Nel caso in cui la funzione

[math]f(x)[/math]
assuma, nell'intervallo considerato, sia valori positivi che valori negativi, calcolare la sua area significa calcolare, separatamente, le sue aree positive e le sue aree negative, e poi sommarle algebricamente.

Calcolo dell'area di una funzione

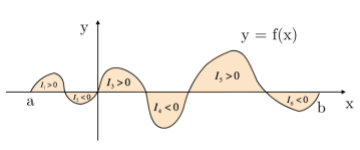
Possiamo dedurre che, in questo caso, il valore dell'integrale definito, e cioè la misura dell'area totale, sarà positivo se le aree situate al di sopra dell'asse delle ascisse hanno estensione maggiore delle aree che si trovano al di sotto, e sarà invece negativo nel caso opposto.

Per ulteriori approfondimenti sugli integrali definiti vedi anche qua

Vuoi approfondire Analisi Matematica – Esercizi, problemi e formule di Analisi Matematica con un insegnante esperto?
Trovalo su Ripetizioni.it