In questo appunto approfondiremo il concetto di logaritmo. Ne riprenderemo la definizione, vedremo alcuni importanti logaritmi, come quello naturale, che ha per base il numero di Nepero, e quello decimale, cioè in base 10. Inoltre, dopo aver dato un'occhiata ai grafici della funzione logaritmica, ci concentreremo su alcuni esempi di calcolo.
.
Dobbiamo, cioè trovare il logaritmo in base 3 del numero 9. Per fare ciò dobbiamo porci la domanda: quale esponente devo assegnare alla base 3 per avere come risultato il numero 9.
Basta conoscere un po' di aritmetica di base per sapere che il numero cercato è 2.
. Dobbiamo cioè risolvere:
.
.
Ricorda anche due cose molto importanti.
[math] \log_a 1 = 0[/math]
Se la base e l'argomento del logaritmo sono uguali, il risultato del logaritmo è sempre 1.
[math] \log_a a = 1 [/math]
Definizione di logaritmo naturale o neperiano
Alcuni logaritmi sono più utilizzati di altri, per cui acquistano dei nomi particolari. Uno di questi, forse il più importante, è il logaritmo che ha per base il numero
[math]e[/math]
. Il numero
[math]e[/math]
(o numero di Nepero) è un numero irrazionale, che vale:
[math] e = 2,71828 \, 18284 \, 59045 \, 23536 \dots [/math]
Un logaritmo la cui base è il numero di Nepero
[math]e[/math]
è detto
logaritmo naturale o neperiano.
Per esso valgono le solite considerazioni:
[math] \log_e 1 = 0 [/math]
[math] \log_e e = 1 [/math]
Definizione di logaritmo decimale o di Briggs
Un altro logaritmo che viene spesso utilizzato è il logaritmo con base 10, detto anche
logaritmo decimale.
Il logaritmo decimale è molto utilizzato per via del fatto che il numero 10 è la base del nostro sistema di numerazione.
[math] \log_{10} a = b \leftrightarrow 10^b=a [/math]
Il logaritmo decimale è noto anche con il nome di logaritmo di Briggs, dall'omonimo matematico britannico e, oltre ad indicarsi con il solito simbolo
[math] \log_{10} a = b [/math]
si può spesso trovare con l'iniziale maiuscola
[math] \text{Log} a = b [/math]
.
Osservazioni
Osservazione 1: Quando si dà una nuova definizione occorre sempre controllare che essa non sia contraddittoria. Nella definizione, viene detto che il logaritmo è precisamente quell'esponente da attribuire alla base
[math]b[/math]
per ottenere il numero
[math]a[/math]
; ciò presuppone che esista uno e un sol numero con tale
proprietà. Effettivamente ciò corrisponde a verità, in quanto
la funzione esponenziale di base [math]b[/math]
è iniettiva, e quindi non esistono due
[math]x[/math]
diversi tali che
[math]x^b=a[/math]

Osservazione 2: Dalla definizione di logaritmo, risulta che la base [math]b[/math]
di un logaritmo deve consistere in un numero reale positivo differente da 1. Questa richiesta, a prima vista complicata, è facilmente spiegata osservando che, sempre per la definizione, deve valere
[math]b^x=a[/math]
: visto allora che
[math]b[/math]
deve essere anche la base di una funzione esponenziale, i valori negativi vanno eliminati a causa di come è definita quest'ultima.
Se invece fosse
[math]b=1[/math]
, avremmo che
[math]a=1^x=1[/math]
indipendentemente dal valore di
[math]x[/math]
, ovvero il nostro logaritmo si ridurrebbe alla funzione
[math]y=1[/math]
. Posto allora
[math]b>0[/math]
,
[math]b>1[/math]
può risultare o
[math]b>1[/math]
o
[math]0 ; i due grafici possibili in questi due casi per la funzione
[math]y=\log_b a[/math]
sono rappresentati nelle immagini precedenti.
Osservazione 3: La definizione di logaritmo
[math] \log_b a[/math]
richiede esplicitamente che risulti
[math]a > 0[/math]
. Ciò è dovuto alla definizione di logaritmo e alle
proprietà della funzione esponenziale. Visto che infatti deve risultare
[math]b^x=a[/math]
e che la funzione esponenziale di base
[math]b[/math]
assume valori solo in
[math]\mathbb{R}^+[/math]
, necessariamente il valore di
[math]a[/math]
sarà positivo.
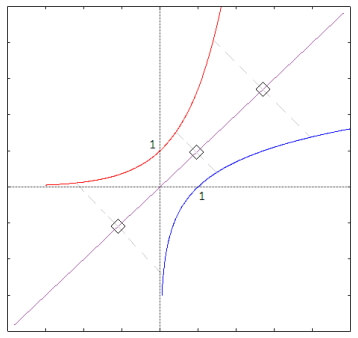
Osservazione 4: Il legame tra funzione esponenziale e logaritmo si può anche visualizzare nel modo che segue.
Si consideri il grafico già noto relativo alla funzione esponenziale di base
[math]b[/math]
(nell'immagine seguente lo si è rappresentato in rosso e si è scelto
[math]b > 1[/math]
) e la bisettrice del primo e terzo quadrante (in viola nel grafico). Riflettendo detto grafico rispetto alla retta data si ottiene il nuovo grafico in blu: esso è il grafico della funzione
[math]y=\log_b a[/math]
, ovvero del logaritmo.
Le proprietà dell'esponenziale valgono riflesse per il logaritmo: se l'esponenziale:
il logaritmo:
In particolare ciò significa che, poiché l'esponenziale possiede un asintoto orizzontale, il logaritmo ne ha uno verticale.
Un legame di questo tipo tra i grafici di queste due funzioni è dovuto al fatto che esse sono una la funzione inversa dell'altra. Nella figura in basso puoi osservare entrambi i tipi di grafici logaritmici.
Per ulteriori approfondimenti sulla funzione logaritmica vedi anche qua
Esempi elementari di calcolo di logaritmi
Esempio 1: Proviamo a calcolare il valore di
[math]x=\log_b 1[/math]
. Come richiesto dalla definizione di logaritmo, per risolvere questo problema dovremo trovare quel valore, che esiste ed è unico in virtù dell'osservazione 1, tale che
[math]b^x=1[/math]
.
Indipendentemente da quale sia la base
[math]b[/math]
, sappiamo che elevandola alla 0 otterremo 1, cioè
[math]b^0=1[/math]
,
[math]\forall b[/math]
. Quindi il risultato sarà
[math]\log_b 1=0[/math]
. In effetti, l'osservazione 4 ci assicurava già che il grafico del logaritmo passa per il punto
[math](1,0)[/math]
quale che sia la base
[math]b[/math]
, cosicché il risultato era in effetti banale.
Esempio 2: Calcoliamo adesso
[math]\log_b b[/math]
. Adoperando ancora la definizione, sappiamo che il numero ricercato deve essere tale che
[math]b^x=b[/math]
. Com'è noto già dalle proprietà delle
potenze, l'elevazione di un numero qualsiasi alla 1 ci restituisce il numero stesso; dunque certamente
[math]\log_b b=1[/math]
per ogni
[math]b[/math]
.
Esempio 3: Utilizzando sempre lo stesso metodo, è possibile verificare i seguenti risultati:
[math] x=\text{Log} 1000\rightarrow x=log_{10}1000\rightarrow 10^x=1000=10^3\rightarrow x=3 [/math]
[math] x=ln \sqrt{e} \rightarrow x = log_e \sqrt{e} \rightarrow e^x = \sqrt{e} = e^{1/2} \rightarrow x = frac{1}{2} [/math]
Esempio 4: Proviamo infine a calcolare il valore di
[math]x=\\log_{2}3[/math]
. Se come al solito ricorriamo alla definizione, scopriamo solo che
[math]2^x=3[/math]
.
Ciò non ci è di grande aiuto, visto che non conosciamo alcun numero
[math]x[/math]
"semplice" che verifichi questa equazione.
Infatti, comunque eleviamo 2 a un numero naturale, otteniamo sempre un numero pari, ed essendo 3 dispari l'uguaglianza non può mai valere.
D'altro canto la funzione esponenziale è definita su tutto
[math]\mathbb{R}[/math]
, quindi una soluzione deve necessariamente esistere. Visto che non la conosciamo con precisione, possiamo quanto meno tentare di approssimarla: visto allora che
[math]2 , è lecito scrivere:
[math]2^1
Questo, unitamente al fatto che la funzione esponenziale è crescente, ci assicura che la
[math]x[/math]
da noi ricercata appartiene all'intervallo
[math](1, 2)[/math]
; in effetti usando una calcolatrice scientifica risulta che
[math]x\approx 1.585[/math]
, e quindi la nostra stima è corretta.
Per ulteriori approfondimenti sui logaritmi, vedi anche qua