Per ulteriori approfondimenti sulle nozioni basilari della statistica, vedi anche qua.
Le medie lasche si differenziano dalle medie ferme, come la media aritmetica o la media geometrica, che invece tengono conto di tutti i valori che costituiscono la distribuzione.
Adesso analizziamo nel dettaglio le due principali medie lasche: la moda e la mediana.
La moda
In questo paragrafo tratteremo della moda matematica, della sua definizione e di alcuni esempi di calcolo.Immaginiamo di avere una distribuzione di
Può accadere che tutti i valori si presentino con la stessa frequenza: in questo caso è evidente come non abbia senso parlare di moda e si concluderà che, per quella distribuzione, la moda non è definita. Allo stesso modo, può accadere che il valore che compare più frequentemente non sia unico, ma che siano due, oppure tre, o più. In questi casi, si parlerà di distribuzioni bimodali, trimodali o, più in generale, multimodali.
A titolo di esempio, consideriamo la seguente distribuzione:
![]()
Salta subito all'occhio il fatto che alcuni valori della distribuzione (il 4, il 67, il 53) compaiano una sola volta, a differenza di altri che, invece, si ripetono. Per calcolare la moda ciò che dobbiamo fare è cercare il valore che compare con frequenza maggiore, cioè più spesso degli altri.
Osserviamo che il valore 23 si ripete per due volte, mentre il valore 10 compare ben tre volte. Il valore che si presenta con frequenza maggiore è, dunque, il 10. Possiamo concludere, dunque, che la distribuzione mostrata è unimodale ed il valore della sua moda è 10.
A questo punto, dovrebbe anche essere chiaro il motivo per cui la moda rientra tra le medie lasche: per determinarla, infatti, non abbiamo tenuto conto di tutti i valori della distribuzione, ma solo di quello che compare più frequentemente.
Come altro esempio, consideriamo la distribuzione, costituita da otto dati:
In questo caso, ci sono due valori (il numero 2 ed il numero 4) che si ripetono entrambi due volte. Si tratta dunque di una distribuzione bimodale.
Un'altra osservazione interessante a proposito della moda è che essa è anche l'unico indice che può essere ricavato anche a partire da una distribuzione di dati non numerici. Supponiamo, per esempio, che nella tua classe venga svolto un sondaggio per il quale ad ogni studente viene richiesto quale sia il suo colore preferito. Supponiamo che 4 studenti rispondano il giallo, 6 studenti il rosso, 8 studenti il blu e i rimanenti 3 studenti rispondano di preferire il nero. Nonostante i dati non siano numeri, come negli esempi precedenti, si può comunque concludere che la moda di tale distribuzione è il colore blu, perché è quello che è comparso, tra le risposte, il maggior numero di volte.
Per ulteriori approfondimenti sulla moda in statistica, vedi anche qua.
La mediana
In questo paragrafo ci occuperemo della seconda media lasca: la mediana. La mediana di una distribuzione è il dato che ne occupa la posizione centrale.A differenza della moda, il calcolo della mediana ha senso solo se la distribuzione presenta esclusivamente valori numerici. Prima del calcolo della mediana è anche richiesto che i valori siano disposti in ordine, generalmente crescente. Vediamo ora la definizione rigorosa di mediana.
Data una successione di
Non sempre in una successione di numeri esiste il valore centrale. Infatti, se il numero di valori di cui è composta la distribuzione è dispari, allora il valore della mediana coincide proprio con quello che occupa il posto centrale della distribuzione. Invece, se il numero di valori è pari, non vi è un valore centrale, e si considera come mediana la media aritmetica dei due valori centrali.
Consideriamo la distribuzione dell'esempio precedente:
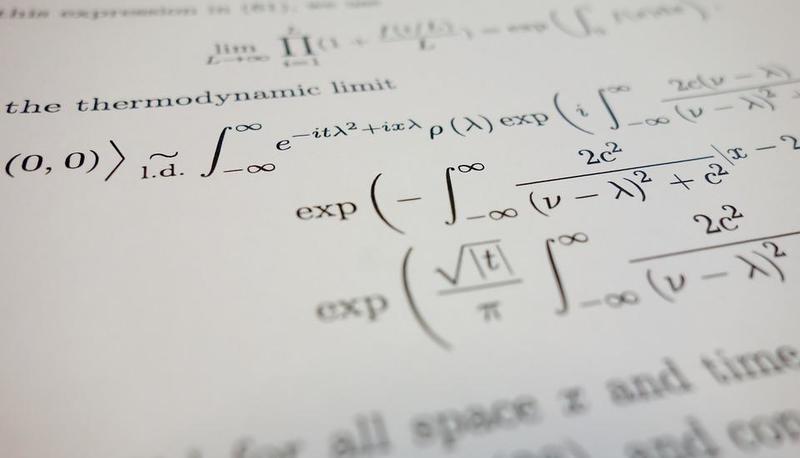
![]()
Poiché in questo caso abbiamo a che fare con un numero pari di dati, non possiamo accedere subito al valore centrale della distribuzione, in quanto non vi è un valore centrale. Come abbiamo visto in precedenza, la mediana è la media aritmetica dei valori che occupano i due posti centrali.
In questo caso, i valori centrali sono 10 e 67, pertanto la mediana sarà data da:
Consideriamo, invece, una distribuzione costituita da un numero dispari di elementi:
![]()
In questo caso, non vi è alcuna difficoltà nella determinazione del valore centrale, in quanto questo è esplicito, ed è proprio pari a 67.
La mediana può anche essere definita come il valore che lascia al di sopra e al di sotto di sé lo stesso numero di termini e che, cioè, divide la distribuzione in due parti.
I quartili
In questo paragrafo accenneremo brevemente ad altri indici di media lasca: i cosiddetti quartili. Così come la mediana divide la distribuzione in due parti, i quartili la dividono in quattro, consentendo quindi un'analisi più precisa del carattere della distribuzione.Spesso è utile conoscere anche termini che dividono diversamente la distribuzione: un esempio sono i cosiddetti quartili. I quartili sono quattro e dividono la distribuzione in quattro parti, proprio come la mediana la divide in due. Più nel dettaglio, abbiamo:
- il primo quartile, cioè il termine che lascia sopra di sé un quarto dei valori e sotto di sé i tre quarti;
- il secondo quartile, che divide la distribuzione a metà, e coincide pertanto con la mediana;
- il terzo quartile, che lascia sopra di sé i tre quarti dei valori e, al di sotto, un quarto dei valori;
- il quarto quartile, che lascia sopra di sé tutti i valori della distribuzione e coincide, quindi, con il termine più alto di questa.
Per ulteriori approfondimenti sugli indici di tendenza vedi anche qua