_stan
di _stan
(320 punti)
8' di lettura
In questo appunto di matematica descriviamo un particolare sistema di coordinate, le coordinate polari. Utili per individuare la posizione di un punto P nello spazio a tre dimensioni. Vedremo inoltre come passare da un sistema all'altro attraverso apposite equazioni della trasformazione, utilizzando le funzioni goniometriche seno e coseno.

Sistemi di coordinate nello spazio, dalle cartesiane alle polari

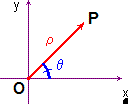
Per individuare un sistema di coordinate polari nel piano, bisogna fissare tre elementi: un punto d’origine, una semiretta orientata e una unità
[math]u[/math]
.
Il punto di origine si chiama polo, e la semiretta orientata si chiama asse polare. Ad ogni punto P del piano vengono associati due numeri: il modulo
[math]\rho[/math]
è l’argomento o anomalia
[math]\theta[/math]
.
Il modulo
[math]\rho[/math]
è la misura di OP rispetto all’unità fissata.
L’anomalia
[math]\theta[/math]
è la misura in radianti, dell’angolo orientato, formato dal segmento OP con l’asse polare
[math]x[/math]
, e preso in senso antiorario.

Coordinate polari nel piano: modulo e anomaliaEsempio di spirale

Diremo allora che un punto P ha coordinate polari:

[math]P\big [\rho; \theta\big][/math]

Per indicare il polo O, scriviamo:

[math]O\big [0; \theta\big][/math]

In modo analogo a quanto avviene nella trigonometria, il segno dell'angolo indica il verso in cui esso è misurato:
se l'angolo è positivo, allora esso è misurato in senso antiorario;
se l’angolo è negativo, allora è misurato in senso orario.
Possiamo quindi affermare che un angolo associato ad un dato punto non è unico, in quanto ogni angolo può essere espresso prendendolo in senso orario o antiorario.
Per esempio il punto P di modulo 1 e anomalia

[math]\theta={\pi \over 4}[/math]
, è anche individuato dalle coordinate polari
[math]\rho=1, \ \ \theta=-{7\pi \over 4}[/math]
, in generale, scriveremo:

[math]\rho=1[/math]

[math]\theta={\pi \over 4}+2k\pi \wedge k\in Z[/math]

Tuttavia, considerando un angolo

[math]\theta[/math]
compreso tra
[math]0[/math]
e
[math]2\pi[/math]
, ad ogni punto P resta associata la coppia di numeri reali
[math]\big [\rho; \theta\big][/math]
che esprimono le sue coordinate, e viceversa, ogni coppia di numeri reali
[math]\big [\rho; \theta\big][/math]
con
[math]0\leq \theta \leq 2\pi[/math]
individua nel piano un solo punto
[math]P[/math]
.
Tale punto può essere individuato come intersezione tra la circonferenza di centro
[math]O[/math]
e raggio
[math]\rho[/math]
e la semiretta avente origine
[math]O[/math]
e formante con l'asse
[math]x[/math]
l'angolo
[math]\theta[/math]
.

Per ulteriori approfondimenti sulle trasformazioni nel piano vedi qua

Trasformazione delle coordinate polari in coordinate cartesiane

È sempre possibile effettuare un cambio di coordinate nel piano cartesiano ovvero si può passare dalle coordinate polari a quelle cartesiane e viceversa mediante opportune equazioni di trasformazione.
Trasformazione di coordinate polari in coordinate cartesiane
Se il polo
[math]O[/math]
coincide con l'origine del sistema di riferimento cartesiano
[math]xOy[/math]
, e se l'asse polare
[math]x[/math]
coincide con il semiasse positivo delle ascisse, e le unità di misura dei due sistemi coincidono, possiamo individuare un metodo per passare dalle coordinate cartesiane a quelle polari, e viceversa.

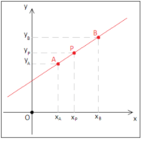
Consideriamo un punto

[math]P[/math]
del piano che ha coordinate cartesiane
[math](x; y)[/math]
e coordinate polari
[math]\big [\rho; \theta\big][/math]
Facciamo riferimento alla figura in alto.
Osserviamo il triangolo rettangolo
[math]OPH[/math]
, possiamo ricavare il valore di
[math]x[/math]
ed
[math]y[/math]
in funzione delle coordinate polari. Ascissa e ordinata del punto P sono i due cateti del triangolo rettangolo, valgono perciò le seguenti relazioni:

[math]OH=x=\rho \cdot cos \theta \ \ e \ \ PH=y=\rho \cdot sin \theta[/math]

Queste formule rappresentano la relazione tra le coordinate polari e le coordinate cartesiane.
Con questi due formulette se è nota la anomalia e il modulo del punto P è possibile calcolare le sue coordinate cartesiane.
Vediamo ora come si trovano modulo e anomalia conoscendo le coordinate cartesiane del punto.
Sviluppiamo alcuni passaggi algebrici.
Eleviamo al quadrato le formule viste in precedenza:

[math]x^2 = \rho^2 cos^2 \theta[/math]

[math]y^2 = \rho^2 sin^2 \theta[/math]

ora sommiamo membro a membro:

[math]x^2 +y^2= \rho^2 \big (cos^2 \theta +sin^2 \theta \big)[/math]

Per la prima relazione fondamentale della goniometria tra seno e coseno sappiamo che:

[math]cos^2 \theta +sin^2 \theta =1[/math]

Perciò possiamo scrivere:

[math]\rho^2 =x^2+y^2[/math]

Da cui ricaviamo il modulo estraendo la radice quadrata di entrambi i membri:

[math]\rho=\sqrt{x^2+y^2}[/math]

Una volta trovata l’espressione del modulo possiamo scrivere anche le funzioni coseno e seno:

[math]cos \theta={x\over \rho}=\frac{x}{\sqrt{x^2+y^2}}[/math]

[math]sin \theta={y\over \rho}=\frac{y}{\sqrt{x^2+y^2}}[/math]

Queste equazioni consentono di passare dalle coordinate cartesiane alle coordinate polari.
Per ulteriori approfondimenti sulle formule goniometriche vedi qua

Grafici in coordinate polari, la spirale

Consideriamo una curva di equazione
[math]y = mx + q[/math]
; sappiamo che, in un riferimento cartesiano, tale equazione rappresenta una retta.
Esempio di spirale
In un riferimento polare, questa equazione lineare, scritta come:

[math]\rho =\theta +1 \wedge \theta \geq 0[/math]

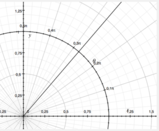
rappresenta una spirale, una curva simile a una molla d’orologio sganciata dai suoi cardini, la spirale ha “origine” nel polo e si avvolge intorno ad un asse perpendicolare al piano x y, in senso antiorario.
In generale, una curva di equazione:

[math]\rho=m \theta +q[/math]

in base al valore di

[math]m[/math]
può rappresentare:
  • una circonferenza con centro nel polo e raggio
    [math]q[/math]
    , con
    [math]\rho\geq p[/math]
    se
    [math]m=0[/math]
    ;
  • una spirale se
    [math]m\neq 0[/math]
In particolare, distinguiamo i casi in cui m sia maggiore o minore di zero.
  • se
    [math]m>0[/math]
    , si ha una spirale che esce dal punto A(q ; 0) e al crescere di
    [math]\theta[/math]
    da zero a
    [math]+\infty[/math]
    si allarga ruotando nel verso antiorario via via più rapidamente a seconda della grandezza di
    [math]m[/math]
    ;
  • se
    [math]m, si ha una spirale che esce dal punto A(q ; 0) e al decrescere di
    [math]\theta[/math]
    da zero a
    [math]-\infty[/math]
    si allarga ruotando in senso orario, più rapidamente a seconda della grandezza di
    [math]m[/math]
    .

    Per ulteriori approfondimenti sui sistemi di coordinate vedi qua

Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it