Valore assoluto o modulo di un numero reale: definizione ed utilizzo

Nel paragrafo seguente verrà data la definizione di valore assoluto di un numero; a seguire verranno enunciate anche le sue proprietà.

Definizione e proprietà

Se è un numero reale, diremo che il suo valore assoluto, e lo indichiamo con , è dato da:

In questa notazione, il numero reale

viene definito argomento del modulo o del valore assoluto.
Il valore assoluto di un numero, quindi, è sempre una quantità sempre positiva o nulla , nel caso in cui l'argomento sia zero. Deduciamo, quindi, che i numeri opposti hanno lo stesso valore assoluto.

N.B. Due numeri hanno lo stesso valore assoluto se sono uguali o opposti.
Dati

e , due numeri reali, valgono le seguenti proprietà:

• [math] |x| |y| = |x \cdot y|[/math]
  ;
• [math] |x+y| \le |x| + |y| [/math]
  ;
• [math] \frac{|x|}{|y|} = \Big| \frac{x}{y} \Big| [/math]
  ;
• [math] |x-y| \ge |x| - |y| [/math]
  .

In realtà, oltre al caso dei numeri reali, possiamo estendere la definizione di valore assoluto anche al caso in cui l'argomento è una generica espressione letterale, che indichiamo con

. In questo caso diremo che, per definizione, il valore assoluto di è pari a:

Nel paragrafo successivo sono presenti delle applicazioni della definizione di valore assoluto per la risoluzione di equazioni e disequazioni semplici.

Risoluzione di equazioni e disequazioni con valore assoluto

Vediamo adesso alcune applicazioni del Valore assoluto per la risoluzione, utilizzando la definizione, di alcuni tipi di equazioni e disequazioni in maniera immediata.
Consideriamo un’equazione del tipo:

sapendo che due numeri reali hanno lo stesso modulo se sono uguali o opposti, l'equazione può essere risolta ponendo:

può essere risolta con lo stesso principio enunciato precedentemente, ovvero:

un valore assoluto è uguale a zero se, e solo se, il suo argomento è nullo, quindi avremo:
.

Vediamo adesso qualche disequazione del tipo:

sono impossibili, perché il modulo di un numero non può mai essere un numero negativo;

hanno come uniche soluzioni quelle date da

;

e (con positivo)
sono verificate per qualunque valore di , poiché il valore assoluto di un numero è sempre positivo.

Quelli visti fin ora sono equazioni o disequazioni con risoluzione immediata. Vediamo adesso qualche applicazione del valore assoluto all’interno di equazioni e disequazioni più complesse.
Consideriamo un’equazione del tipo:

. In questo caso figura un solo valore assoluto e, secondo la definizione di valore assoluto, abbiamo che:

Per risolvere questa equazione, quindi, dobbiamo risolvere il seguente sistema:

Pertanto risolviamo i due sistemi, tenendo presente che si tratta di sistema misto, cioè un sistema composto da un’equazione e una disequazione:

La soluzione del sistema è quindi

poiché nel primo sistema otteniamo la stessa soluzione (), mentre nel secondo sistema la soluzione è impossibile.
Vediamo ora un altro esempio in cui nell'equazione compaiono due valori assoluti, ovvero:

Cominciamo studiando il segno degli argomenti dei valori assoluti. In particolare, abbiamo:

per il primo valore assoluto;

per il secondo valore assoluto.

Per capire meglio come procedere, rappresentiamo quanto ottenuto in uno schema/diagramma, dove: le linee tratteggiate rappresentano i tratti in cui l'argomento è negativo, mentre le linee piene/continue rappresentano il tratto in cui l’argomento è positivo. Adesso assegniamo un nome a ciascun intervallo per capire in quale zona dello schema ci troviamo, in particolare li chiamiamo rispettivamente:

e .

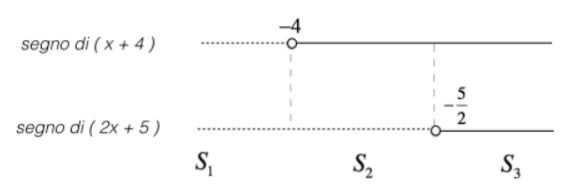
Per ogni intervallo individuato dobbiamo risolvere un sistema, in cui avremo una disequazione, data dall'intervallo in cui ci troviamo, e un'equazione in cui gli argomenti dei valori assoluti assumeranno il segno che hanno in quell'intervallo.

Cominciamo dal primo intervallo, dove avremo entrambi i valori assoluti con segno negativo, ovvero:

Per questo intervallo dobbiamo risolvere il seguente sistema:

concludiamo quindi che:

Passiamo al secondo intervallo abbiamo che il segno del primo valore assoluto è positivo, mentre quello del secondo valore assoluto è negativo, quindi:

Per questo intervallo, il sistema da risolvere sarà:

La soluzione dell'equazione non soddisfa la disequazione, quindi concludiamo che:

Concludiamo con il terzo intervallo dove entrambi i valori assoluti hanno segno positivo, quindi avremo:

Il Sistema corrispondente è:

La soluzione dell'equazione è accettabile, quindi concludiamo che:

Queste soluzioni valgono all’interno di ciascun intervallo, quindi la soluzione generale dell'equazione di partenza, è data dall'unione delle soluzioni di tutti gli intervalli, cioè:

Nel paragrafo successivo sono presenti degli approfondimenti ed ulteriori esempi sul valore assoluto all’interno di equazioni e disequazioni.

Potrebbero interessarti

• Disequazioni con valore assoluto
• Videolezione: Equazioni con il modulo o valore assoluto
• Esercizi svolti sulle equazioni