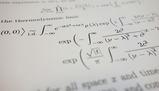Dietro ogni conquista scientifica c sempre un lavoro estenuante, una dedizione assidua e un incrollabile desiderio di superare i limiti. Molto spesso il vero problema non rappresentato dalla complessit di risoluzione matematica o dalla difficolt costruttiva di strumentazione, ma dalla necessit di attivare nuovi modi di pensare e abbandonare consolidate e rassicuranti certezze.
La storia della scienza un susseguirsi di brillanti intuizioni.
Un esperimento, prima di divenire un inattaccabile modello matematico, soprattutto uno straordinario momento creativo, un atto rivoluzionario del pensiero che abbandona il familiare sentiero della conoscenza, per imboccarne un altro con coraggio ed estroso ingegno.Col senno di poi, tutto sembra naturale, quasi scontato, ma senza quellintuizione illuminante, senza quel cambio di punto di vista, nulla sarebbe stato possibile.
Il valore di unintuizione determinante. E ancora pi determinante se applicata a fenomeni che esulano dalla nostra scala di osservazione dove gli eventi sembrano seguire leggi deterministiche e grazie alle quali possibile prevedere il comportamento di un sistema fisico in modo esatto, conoscendo il suo stato ad un istante di tempo iniziale. Perci, non finir mai di stupire il salto concettuale indispensabile per comprendere linfinitamente piccolo e linfinitamente grande. Linevitabile cambio di paradigma necessario per intuire, osservare e interpretare cosa accade in quella scala di tempi e grandezze, rappresenta uno sforzo intellettuale impareggiabile.
In questo articolo voglio sottolineare uno di questi momenti di geniale creativit, uno dei tanti significativi sforzi intellettuali: lequazione di Born-Oppenheimer, grazie alla quale stato possibile semplificare lo studio dellequazione di Schroedinger rendendola, cos, praticabile.
Unintuizione geniale un faro che illumina lesistenza, qualunque sia lambito di applicazione. Per quanto la realt dei fenomeni macroscopici possa ingannevolmente indurre a pensare che ci che pu essere facilmente osservato, e in alcuni casi toccato, sia relativamente pi semplice da studiare e interpretare, sarebbe sbagliato concludere che, ad esempio, le intuizioni di Galileo sul moto dei corpi siano state pi agevoli poich suffragate da sensate esperienze, mentre le intuizioni di chi indaga il submicroscopico siano pi complesse poich, in quel contesto, i sensi sono pesantemente invalidati. In entrambi casi stata necessaria unacrobazia della mente, un capovolgimento del senso comune.
Tuttavia, a chi come noi osserva da distante spettatore il mondo delle particelle elementari, potendone studiare le manifestazioni soltanto sui libri e sforzandosi con fatica di immaginare la concreta realizzazione di un esperimento, le acrobazie intellettuali dei fisici quantistici appaiono come sconvolgenti conclusioni.
Rivolgendo lattenzione alla struttura microscopica della materia, ci sembra che ogni cosa perda di logica: il certo cede il posto al probabile, losservazione altera e disturba loggetto osservato. Di fronte alla scala di grandezze atomiche non solo necessario utilizzare leggi fisiche diverse da quelle del mondo macroscopico, ma soprattutto necessario smettere di pensare in modo simile a come viene naturale pensare dinanzi alla realt che abbiamo sotto gli occhi.
Lequazione di Schroedinger lequivalente dellequazione di Newton nella descrizione del mondo fisico microscopico. E unequazione molto simile a quella di DAlembert per le onde classiche e descrive levoluzione di un certo stato iniziale, definendo cos la funzione donda ad ogni istante.
Le funzioni donda sono strutture matematiche molto complesse. In generale, sono funzioni delle coordinate di tutti gli oggetti in gioco, cio elettroni e nuclei, del sistema in studio, il che rende lequazione di Schroedinger impossibile da risolvere in modo esatto per sistemi realistici. Esistono diverse approssimazioni possibili, ma la pi utile di certo quella di Born-Oppenheimer, in base alla quale possibile scindere lequazione in due distinti problemi: un problema elettronico e un problema nucleare. Tale approssimazione possibile poich il moto dei nuclei e quello degli elettroni si sviluppano su scale cronologiche molto distanti, dato che i nuclei possono arrivare ad essere pi pesanti degli elettroni di parecchie migliaia di volte. E ragionevole quindi considerare i nuclei come fissi nello spazio e concentrarsi esclusivamente sugli elettroni. In un secondo momento, se necessario, si passer a studiare il moto dei nuclei.
Noi facciamo fatica a dare concretamente forma a realt cos microscopiche; ci sforziamo di capire come sia possibile separare il moto di oggetti le cui dimensioni sono inferiori alla centesima parte del milionesimo di centimetro e la cui durata di vita, a volte, si consuma in tempi cos brevi che non sarebbero misurabili con nessuno dei cronografi a nostra disposizione, ma ci rendiamo perfettamente conto di essere di fronte allennesima acrobazia dellintelligenza.
Domenico Signorelli