(90 punti)

28' di lettura

4 / 5 (2)

Dal teorema di De Giorgi - Nash al teorema di Pitagora: un salto a ritroso di venticinque secoli segnati dalla costante ricerca della verità scientifica

Domenico Lenzi (Dip. Mat.Univ. del Salento)

Sunto: Intorno al 600 a. C., grazie a Talete (cfr. [T] a pag. 13 ed [M] a pag. 3), iniziò un lento processo di razionalizzazione della geometria, che ebbe il suo momento più alto con Euclide: nacque così la Scienza. Pitagora, da molti ritenuto allievo di Talete, fu uno dei principali artefici di quel processo.

Recentemente è stata ricordata la figura di John Forbes Nash Jr., matematico americano il cui nome è legato a quello del nostro Ennio De Giorgi in un importante teorema sul calcolo delle variazioni.
Il presente articolo è dedicato a questi studiosi, che hanno segnato tappe fondamentali per la storia della matematica e della scienza.

Abstract: This paper is dedicated to theorem of De Giorgi-Nash and to theorem of Pythagoras.

1. Premessa

L'Oscar attribuito alcuni mesi fa al film "A beautiful mind" - che narra con qualche spunto arbitrario la vita di John Forbes Nash Jr., matematico americano tuttora vivente, insignito nel 1994 del premio Nobel per l'Economia, mentre per la Matematica il Nobel non è previsto - ha risvegliato attenzioni sopite da tempo nei riguardi di numeri, figure geometriche e ogni altra cosa legata a loro. E forse mai come quest'anno ci sono state tante richieste di partecipazione alle Olimpiadi di Matematica per la scuola media, organizzate da enti vari e associazioni quali Mathesis, C.I.I.M., Sc. Normale Sup. di Pisa, Universita' "Bocconi", ecc.

Misurare e far di conto sono sempre state attività tipiche dell'umanità. E' vero che nella Bibbia si legge che il Padreterno nel corso della creazione contò fino a sei giorni e poi si riposò; ma Dio la matematica non la fa, Lui è la matematica, Lui è la ragione, è tutto.
Inoltre si conoscono casi in cui animali hanno mostrato una certa, anche se rozza, parvenza di attività matematica; ma - a parte alcuni fenomeni da baraccone in cui trucchi occulti l'hanno fatta da padrone - si è sempre trattato di casi estremamente elementari in cui la matematica ha fatto appena capolino e, come "etichetta", è stata usata impropriamente.
Generalmente è considerato emblematico il comportamento del cuculo che va a deporre il suo uovo in un nido non suo, però premurandosi di sostituirlo a un altro - inquilino legittimo - che fa precipitare, per evitare che il vero proprietario del nido si renda conto dell'intrusione. Ma forse il suo è solo un fatto istintivo governato dal suo DNA e non, come qualcuno ha detto, un esempio di abilità aritmetica. Meno noto è il taglifo, un animaletto che quando ritorna alla sua tana lo fa secondo un percorso in linea retta. Conosce la geometria il taglifo? Noi non lo crediamo. Con ogni probabilità anche lui si limita semplicemente a seguire il suo istinto. Però per l'uomo le cose stanno in maniera diversa; e su di un terreno in cui intuito e istinto sono un concime basilare, spesso si innesta un'attività di tipo razionale in cui l'eccitazione (se così si può dire) di zone tipiche del cervello umano è essenziale.
Ebbene nell'ambito della disciplina matematica - purtroppo spesso mal digerita e mal sopportata da molti studenti, anche per colpa di insegnanti non adeguatamente preparati da una università che sembra andare verso il baratro (ma questo è un altro discorso) - con ogni probabilità il risultato più noto è rappresentato dal Teorema di Pitagora: Il quadrato costruito sull'ipotenusa di un triangolo rettangolo è equivalente all'unione dei quadrati costruiti sui cateti.
D'altro canto il teorema di De Giorgi-Nash ha rappresentato uno dei risultati più importanti degli ultimi cinquant'anni; cercheremo di vederne il perché.

2. Un recente passato

Come molti sapranno, Nash meritò il Nobel per i suoi risultati sulla Teoria dei Giochi.
Ma cos'è questa teoria dal nome strano, che fa pensare più a una sala fumosa dove si pratica il gioco d'azzardo che non alla stanza di lavoro - spesso disordinata e caotica (per gli altri!) - di uno scienziato?
Gianfranco Gambarelli - uno dei principali esperti italiani e fondatore della scuola italiana di Teoria dei Giochi, che ha avuto modo di collaborare con Nash (in proposito risulta molto intrigante l'ultimo capoverso di [Ga2], intitolato La busta gialla) - ha brevemente illustrato, ancora in [Ga2] (ma in proposito si può consultare anche il suo testo [Ga], di lettura facile e gradevole): La Teoria dei Giochi è la scienza matematica che analizza situazioni di conflitto e ne ricerca soluzioni competitive e cooperative. Le applicazioni e interazioni di tale teoria sono molteplici: dal campo economico a quello militare, biologico, sociologico, psicologico.
Quella di Nash è stata una vita davvero travagliata, soprattutto per la sua schizofrenia, che ha inevitabilmente determinato per lui alcune incomprensioni nell'ambito del mondo accademico e qualche delusioni professionale. Una di queste delusioni riguardò il celebre teorema di De Giorgi-Nash sul calcolo delle variazioni, dimostrato nel 1957 - alcuni mesi prima di Nash, tra l'altro in modo più semplice ed elegante - da Ennio De Giorgi (cfr. [Gi], [Gi1] ed [L]), insigne matematico pugliese morto nel 1996, che fu professore presso la Sc. Normale Sup. di Pisa ed ha attivato presso l'Università di Lecce (sua città natale) una fiorente scuola sul calcolo delle variazioni, disciplina di cui egli è stato uno degli studiosi più importanti.

Ma cosa dice il teorema di De Giorgi-Nash? Senza scendere in complicati dettagli tecnici - che esulano dallo scopo di queste brevi considerazioni e potrebbero risultare in parte incomprensibili - rinviamo a [Gi] (e agli altri interventi che accompagnano [Gi]) chiunque fosse interessato anche a un minimo di approfondimento sull'attività scientifica del nostro Ennio. Qui ci limitiamo a segnalare che questo teorema si riferisce alla regolarità di un certo tipo di funzionali.
Invece per quel che riguarda il calcolo delle variazioni, riportiamo le parole che De Giorgi stesso e due suoi allievi, Giuseppe Buttazzo e Gianni Dal Maso, hanno scritto sull'Enciclopedia Treccani del Novecento: … rientrano nel calcolo delle variazioni tutti i problemi in cui si cerca il minimo o il massimo di una certa grandezza. … In esso rientrano molte questioni sia di matematica pura sia di matematica applicata alla Fisica, all'ingegneria, alla Biologia, all'Economia.
Quanto è stato richiamato or ora in qualche modo dovrebbe far capire l'importanza del calcolo delle variazioni per la Teoria dei Giochi, poiché nelle funzioni a più variabili proprietà di minimo e nello stesso tempo di massimo sono spesso legate ai "punti di sella", che generalmente caratterizzano situazioni di equilibrio, che hanno notevole importanza in Teoria dei Giochi (dove segnaliamo i cosiddetti "equilibri di Nash").
A proposito delle dimostrazioni del teorema di De Giorgi-Nash, Enrico Giusti - che insieme a De Giorgi e a Enrico Bombieri [Bombieri è l'unico matematico italiano a cui sia stata assegnata (1974) la Medaglia Field] ha dato importanti contributi al calcolo delle variazioni - in [Gi] ha scritto: Il metodo di Nash, totalmente differente da quello di De Giorgi, era molto più complesso e non ha avuto sviluppi. Non così quello di De Giorgi, che è stato il punto di partenza per innumerevoli ricerche, e il cui potenziale non si è ancora esaurito.
E Antonio Leaci, anche lui allievo dell'insigne maestro salentino, in [L] ci rivela: Le loro dimostrazioni erano completamente diverse, così come lo erano i loro caratteri e i loro modi di lavorare: competitivo e individualista Nash, prodigo ed estimatore del lavoro in collaborazione De Giorgi.
Il teorema di De Giorgi-Nash è legato al 19° dei 23 fondamentali problemi di matematica presentati da David Hilbert durante il famoso Convegno dell'Unione Matematica Internazionale svoltosi a Parigi nel 1900.
Prima di De Giorgi molti altri studiosi si erano cimentati con quel 19° problema, fornendo soluzioni parziali. Con De Giorgi - e dopo alcuni mesi, in maniera indipendente, con Nash - il problema fu completamente risolto.
De Giorgi ha fornito contributi determinanti anche per lo studio del 20° e del 23° di quei problemi, anche questi sul calcolo delle variazioni.
Tornando a Nash, c'è da ricordare che la sua è stata solo una delle tante vite travagliate di matematici. Ricordiamo per tutti i grandi Renato Caccioppoli e Alan Turing, morti suicidi durante il secolo scorso, ai quali sono stati dedicati rispettivamente i film "Morte di un matematico napoletano" e il recente "Enigma". Grandi menti le loro, ma purtroppo (come si è verificato per molti matematici eccelsi) con seri problemi.
Qualcuno ha detto che la razionalità confina con la pazzia; e forse questo è in parte vero. Probabilmente per alcuni studiosi un eccessivo chiudersi in se stessi e nei propri problemi scientifici a volte irrisolubili, coniugato con una certa mancanza di elasticità e con la continua e giustificabile lotta contro il "così è se vi pare" imperante - che pure, in piccole dosi, talora potrebbe essere una sorta di valvola di sfogo - spesso può determinare esiti dirompenti e una certa repulsione da parte degli "altri" anche sul piano personale, oltre che su quello scientifico. Perciò si dovrebbe cercare di porre preventivo rimedio, specialmente in ambito didattico, a questi inconvenienti legati alla razionalità, che tuttavia - è bene ricordarlo - caratterizza le funzioni più elevate dell'essere umano ed ha nell'attività matematica la sua massima espressione.

2. Un'intrigante dimostrazione

Il celebre teorema di Pitagora, anche se la sua origine è incerta, in qualche modo era conosciuto già prima che il grande matematico ne facesse il caposaldo della sua famosa scuola. Però prima di allora quel risultato era qualcosa di estremamente empirico, legato a particolari esigenze concrete, quali - ad esempio, prima dell'avvento dell'impero di Alessandro Magno - la costruzione di altari in India (si veda [Bt], p. 548 e segg.); invece con Pitagora esso assunse il ruolo di un teorema, con la presa di coscienza del suo valore universale e non limitato ad alcuni casi, seppur significativi. Il che caratterizzò gran parte della geometria allora conosciuta, principalmente a partire da Talete (circa 7°-6° sec. a.C.) e Pitagora - forse allievo di Talete - che diedero inizio storicamente a quel processo di razionalizzazione della geometria, che trovò la sua massima espressione negli "Elementi" di Euclide (circa 4° sec. a.C.).

Di questo teorema la storia della matematica non ci fornisce una dimostrazione che sia attribuibile a Pitagora o ad altri matematici del suo tempo, anche perché non abbiamo documenti risalenti a quel periodo. Infatti le prime informazioni sul periodo ellenico degli studi di matematica sono giunte a noi attraverso gli scritti di Proclo (circa 5° sec. d.C.), il quale - come ci ricorda Maracchia in [M] (si veda nota ⁽⁵⁾ a pié di pagina 3) - attinse, forse in via indiretta, le sue notizie da Eudemo di Rodi (4° sec. a.C.).
Comunque Proclo fa presente che Talete per la sua attività scientifica trasse spunto da quanto allora era in parte già conosciuto in Egitto; infatti egli scrive (si veda ancora [M], p. 3): Talete per primo essendo andato in Egitto, porto' questa scienza, ed egli trovò molte cose, e di molte indicò i principi a coloro che vennero dopo di lui …. E lo stesso Aristotele conferma la possibilità della presenza di una scienza di tipo speculativo in Egitto nel periodo che precede il fiorire in Grecia della geometria (o, come sottolinea lo Struik in , p. 39, nella tarda tradizione egizia tramandataci dai Greci). Infatti, come si legge in [Bt], p. 547, il sommo filosofo greco scrisse: … sviluppatesi oramai le arti pratiche in modo da provvedere adeguatamente ai bisogni materiali della vita, ha potuto sorgere in Egitto una di quelle scienze che non sono rivolte a fini utilitari, essendo ivi la casta sacerdotale in possesso dell'otium necessario alla ricerca disinteressata.
Tornando al teorema di Pitagora va detto che di esso col passare dei secoli sono state "sfornate" dimostrazioni in quantità copiosa. Tra l'altro, una di queste è attribuita a J. A. Garfield, che fu presidente degli U.S.A. Carmine Mazzei, presidente della sezione Mathesis di Crotone - patria adottiva di Pitagora, ove questi giunse fuggitivo da Samo verso il 520 a.C. e ove fondò la sua famosa scuola - ha raccolto diverse centinaia di tali dimostrazioni e conta di trovarne altre ancora.
A ogni modo io ho acquisito la convinzione, per le ragioni che saranno esposte nel seguito, che Pitagora stesso non può non aver avuto la "prova provata" - come a volte si dice in altri contesti - di quel formidabile risultato, divenuto fondamentale per la geometria e per la visione del mondo che ci circonda, dato che essa era sotto i suoi occhi.

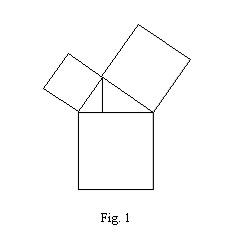
Molti si domanderanno dove sia questa dimostrazione del teorema. Ebbene, essa è qui sopra, nella figura che generalmente rappresenta - ma anche dimostra immediatamente, se la si legge in modo opportuno - quanto il teorema afferma.
Ciò che serve allo scopo sono soltanto alcune nozioni di carattere concreto che ai tempi di Pitagora erano senz'altro patrimonio strumentale ben consolidato anche per artigiani e cultori di arti quali i pittori e gli scultori. Ci riferiamo agli ingrandimenti senza deformazioni - cioè che conservano le forme - secondo un fattore di scala (in breve: le similitudini); per i quali, date due figure piane A e B che siano in un certo rapporto p, quel rapporto si mantiene tra quelle stesse figure ingrandite.
La nostra affermazione è avvalorata dal fatto che considerazioni di questo tipo venivano certo fatte in quel periodo, sia prima che dopo Pitagora, per ricavare proprietà fra le figure tramite considerazioni legate alle simmetrie e alle similitudini (cfr. [M2]); per esempio, in riferimento al rapporto costante tra cerchio e quadrato ad esso circoscritto.
Simplicio ci ha conservato un lungo brano della Storia della Geometria (non pervenutaci), che risulta essere la fonte autentica più antica di Storia della Matematica giunta fino a noi (cfr [Ti], p.44) di Eudemo di Rodi, in cui Eudemo dice di Ippocrate di Chio (da non confondere con l'omonimo a cui si attribuisce il giuramento dei medici) vissuto intorno al 450 a.C., quindi solo qualche decina di anni dopo Pitagora: Egli assumeva … : segmenti circolari simili stanno fra loro come i quadrati delle loro basi. Ciò egli provava col dimostrare che i quadrati dei diametri stanno fra loro come i loro circoli (si veda [Ti], p. 45).
Quindi Ippocrate si esprime seguendo un'impostazione che sembra incanalarsi, anche se in forma meno intuitiva e immediata, nel solco in cui io sono portato a pensare che si sia mosso Pitagora. D'altro canto è proprio quell'immediatezza che mi fa presumere che la prova del teorema sia in fig. 1, in quel disegno mal riuscito di un bambino privo di fantasia; in quella strana casetta dal tetto sghimbescio e con due grossi camini di foggia quadrata che lo ricoprono completamente; priva di porte e finestre, ma con quella linea verticale che divide il tetto, chiave di volta della dimostrazione. Infatti la figura espressa dalla casetta priva dei due camini rappresenta un ingrandimento secondo un certo fattore di scala della figura costituita dalla parte triangolare sinistra del tetto e dal camino sovrastante; potendosi dire la stessa cosa rispetto all'analoga parte situata a destra. Il che giustifica le eguaglianze riportate successivamente in (2). Allora un semplice calcolo dimostra il teorema.
Ma quale calcolo ci sarà mai stato per il nostro Pitagora? In verità forse per lui non ci fu calcolo alcuno, ma solo un'intuizione improvvisa, una visione immediata; una di quelle cose che ti danno una scarica di adrenalina e ti mozzano il fiato. Come dirlo meglio? Forse più adatte sono le parole con cui Sergio Frau descrive la formidabile intuizione che lo ha portato a concepire le Colonne d'Ercole sul Canale di Sicilia piuttosto che sullo Stretto di Gibilterra, dando così finalmente senso a molte affermazioni sulla geografia dell'antica Grecia (si veda "Le Colonne d'Ercole" Edizioni Nur Neon, 2OO2): ... è stato un flash, un lampo: roba di un attimo, di quella che, però, ti buca gli occhi, ti mette gli spilli nella schiena, ti scioglie le ginocchia, ti cambia lo sguardo. E ancora: ... è bastato un attimo: è stato lo spettacolo più maestoso e possente che si possa immaginare. Come raccontarlo? Inimmaginabile se non lo si vede.
Ma proviamo a raccontarla questa dimostrazione del teorema di Pitagora, però riconducendola alle aree interessate. Perciò chiamiamo T l'area del nostro triangolo rettangolo, nonché T1 e T2 le aree del triangolo sinistro e di quello destro in cui il primo è suddiviso dalla sua altezza relativa all'ipotenusa (si veda fig. 1), da cui segue la seguente eguaglianza, fondamentale per la dimostrazione che stiamo per presentare:

(1) T = T1 + T2.

Inoltre chiamiamo Q l'area del quadrato costruito su quell'ipotenusa e rispettivamente Q1 e Q2 le aree costruite sul cateto di sinistra e su quello di destra. In fine, per quanto già detto in precedenza, poniamo:

(2) p = Q/T = Q1/T1 = Q2/T2.

Allora da T = T1 + T2 si ricava subito p*T = p*T1 + p*T2; cioè:

Q = Q1 + Q2.

Tutto qui!

Appendice. Per maggior completezza osserviamo che le eguaglianze in (2) discendono in modo attualmente più esauriente dalle formule con cui si calcola l'area di quadrati e triangoli. Infatti se denotiamo con i, i1, i2 le lunghezze delle ipotenuse dei triangoli considerati e con h, h1, h2 le lunghezze delle altezze relative alle ipotenuse degli stessi, allora si ottiene:

Q/T = 2i/h, Q1/T1 = 2i1/h1, Q2/T2 = 2i2/h2.

Perciò le eguaglianze in (2) sono ovvie anche per la similitudine dei triangoli considerati.

Per concludere, si fa presente che diversi autori hanno cercato di capire quale possa essere stata la dimostrazione di Pitagora. Tra questi Sir Thomas Heat presenta in [H] (pp. 148 e 149) tre proposte delle quali la seconda si avvicina molto a quella illustrata precedentemente, poiché anch'essa si basa sull'eguaglianza (1) e sulle similitudini richiamate. Tuttavia la dimostrazione di Heath risente - come quella legata alla prima parte di quest'Appendice - della mediazione di una proprietà che, per quanto semplice, non consente di raggiungere l'immediatezza espressiva della dimostrazione qui presentata originariamente [Tale proprietà - da cui seguono subito le eguaglianze espresse in (2) - rientra nella Proposizione 19 del Libro VI di Euclide che afferma (si veda [E], p. 386): I triangoli simili stanno fra loro in rapporto duplicato di quello dei lati omologhi (cioè, dei quadrati costruiti sui lati omologhi; n.d.a.)].
Cerchiamo di spiegare meglio il senso di queste parole. Ebbene ci sono dimostrazioni, anche semplici ed elementari come le due precedenti, che pur tuttavia si riferiscono ad affermazioni che in realtà "a priori" sono delle congetture, magari altamente verosimili sulla base di indizi numerosi e significativi. Ci sono poi dimostrazioni che non sono altro che la traduzione immediata di un'intuizione, della visione di una proprietà attraverso la percezione del relativo percorso dimostrativo. Come esempio significativo ricordiamo il "teorema dei carabinieri" sulla convergenza di funzioni reali. Orbene, sulla base di quanto espresso in questo articolo, noi presumiamo che Pitagora ad un certo punto si sia trovato proprio nel secondo tipo di situazione.

Bibliografia

[Bt] Bortolotti E. (1972) Storia delle Matematiche elementari, in: Enciclopedia delle Matematiche elementari e complementi (a cura di L. Berzolari), Hoepli, Milano.

Boyer C. B. (1968) A history of mathematics, J. Wiley, N. York.
[E] Euclide (1970) Gli Elementi, a cura di A. Frajese e L. Maccioni, U.T.E.T., Torino.
[F] Frajese A. (1969) Attraverso la storia della matematica, Le Monnier, Firenze.
[Ga] Gambarelli G. (1997) Giochi competitivi e cooperativi, Padova, Cedam.
[Ga1] Gambarelli G. (1999) Una testimonianza personale su John Nash, Periodico di Matematiche, 2.
[Ga2] Gambarelli G. (2002) John Nash dal Nobel all'Oscar, Didattica delle Scienze, 219.
[Gi] Giusti E. (1998) Le equazioni alle derivate parziali e le superfici minime, in: Lettera matematica - pristem (dossier pristem), 27-28, p. XVIII.
[Gi1] Giusti E. (2000) Il contributo di Ennio De Giorgi (1928-1996) al calcolo delle variazioni, in: Per Ennio De Giorgi, a cura del Dipart. di Matematica dell'Università di Lecce, Liguori Editore, Napoli.
[H] Heath T. (1981) A history of greek mathematics (vol. I), Dover Publications, Inc., New York.
[L] Leaci A. (2002) Ennio per primo sulla cima del monte, il Corsivo (settimanale del Salento), 11.
[L1] Loria G. (1929) Storia delle Matematiche, Torino, Sten.
[M] Maracchia S. (1975) La matematica come sistema ipotetico-deduttivo (profilo storico), Firenze, Le Monnier.
[M1] Maracchia S. (1969) Sulla genesi della geometria razionale, Archimede, 1 e 2.
[M2] Maracchia S. (1971) Talete nello sviluppo della geometria razionale, Cultura e Scuola, 37.
Struik D. J. (1981) Matematica: un profilo storico, Bologna, il Mulino.
[T] Trudeau R. (1991) La rivoluzione non euclidea, Torino, Bollati Boringhieri.
[Ti] Timpanaro Cardini M. (1962) Pitagorici, Testimonianze e Frammenti, Fasc. II, Firenze, La Nuova Italia.
[V] Veljan D. (2000) The 2500-old Pythagorean Theorem, Math. Magazin, 4.