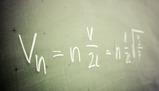Richiami teorici
Si ricorda che la derivata non è altro che il coefficiente angolare della retta tangente ad un punto qualsiasi, e che si può andare ad individuare attraverso la seguente relazione matematica:
[math]m=\lim_{x \to h_0} f(\frac{f(x_0+h)-f(x_0)}{h})[/math]
Questo limite viene definito come Derivata della funzione nel punto
[math]x_0[/math]
. La derivata di una funzione [math]f(x)[/math]
nel punto [math]x_0[/math]
, definita anche come [math] f'(x)[/math]
o [math]\frac{df}{dx}[/math]
o [math]D_x(f)[/math]
, non è altro che il limite del rapporto incrementale, dove l'incremento tende a zero.
[math]f'(x_0)=\lim _{ h\rightarrow 0 }{ \frac{f(x_0+h)-f(x_0)}{h} } [/math]
Il concetto di singolarità di una funzione
Quando si studia una funzione è importante andare a conoscere le proprietà di questa funzione. Quando si procede allo studio della campo di esistenza di una funzione si va definire l'insieme di esistenza, in cui la funzione effettivamente esiste. Ma che cosa succede se la funzione è definita in tutti i punti tranne in uno? In questi casi si parla di punti di singolarità della funzione, in cui la funzione localmente non esiste, ma se si procede allo studio del calcolo del limite in quel punto è possibile andare ad individuare una particolare caratteristica della funzione man mano che questa si avvicina al punto singolare. Le caratteristiche possono essere andamenti all'infinito, andamenti asintotici e così via. Da qui dunque si comprende come sia importante studiare la continuità e discontinuità di una funzione matematica.
Definizione di Continuità di una funzione
Una funzione è continua se questa può essere tracciata sul foglio senza staccare la penna o interrompere il tratto di stesura. Questa è la definizione informale della continuità di una funzione. Di seguito verrà enunciata la definizione formale di continuità. Si consideri una funzione[math]y=f(x)[/math]
, e si voglia studiare la continuità della funzione. La funzione è definita continua in un punto se il limite della funzione per [math]x[/math]
tendente al punto considerato è uguale al valore che la funzione assume ne punto stesso.In termini matematici la continuità di una funzione viene espressa come segue:
[math]\lim_{x\to x_0}[f(x)]=f(x_0)[/math]
Questa relazione deve valere anche quando si va a considerare però l'esistenza del limite. Un limite esiste se e solo se il limite destro e il limite sinistro sono uguali tra di loro. Da cui, si conclude che la funzione è continua nel punto considerato anche se e solo se il limite destro della funzione per
[math]x[/math]
tendente al punto considerato è uguale al il limite sinistro della funzione per [math]x[/math]
tendente al punto considerato, e questi due limiti siano uguali al valore che la funzione assume ne punto stesso.
Concetto di discontinuità
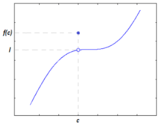
Seuna funzione non risulta essere continua in quel punto, può significare che quel punto risulti essere un punto di discontinuità, o meglio detto punto di singolarità. Esistono tre diverse tipologie di specie di discontinuità di una funzione.
- Discontinuità di prima specie: la funzione presenta un salto finito in corrispondenza del punto di singolarità. Il limite destro e sinistro sono finiti e diversi, pertanto si conclude che il limite non esiste
- La Discontinuità di seconda specie: la funzione presenta un salto infinito in corrispondenza del punto di singolarità. Il limite destro e sinistro divergono e sono diversi, pertanto si conclude il limite non esiste, però funzione ammette un asintoto per [math]x=a[/math]. Per approfondimenti sul concetto di asintoto vedi qui
- La Discontinuità di terza specie: la funzione manca di un solo punto, ovvero nel punto di singolarità considerato. Il limite destro e sinistro sono finiti e uguali, pertanto si conclude che il limite esiste, però la funzione invece nel punto localmente non esiste, ovvero in [math]x=a[/math].
Relazione tra continuità e derivabilità
- Si consideri una funzione [math]y = f(x)[/math], se la funzione è derivabile nel punto[math]x_0[/math], allora la funzione sarà certamente continua in quel punto.
- Si consideri una funzione [math]y = f(x)[/math], Se la funzione è continua nel punto[math]x_0[/math], allora non è detto che la funzione sia derivabile in quel punto.
- La continuità è una condizione necessaria affinché la funzione sia derivabile.
- La derivabilità è una condizione sufficiente affinché la funzione sia continua.
- La continuità in un punto [math]x_0[/math]non garantisce che nel medesimo punto sia anche derivabile. Tuttavia, non essendo continua in[math]x_0[/math], non sarà neppure derivabile in[math]x_0[/math].
Per ulteriori approfondimenti sulla continuità di una funziona vedi anche qua
Il concetto di derivabilità
Una funzione affinchè sia derivabile deve risultare continua, per come è stato definito precedentemente. Esiste però un ulteriore vincolo affinché una funzione sia derivabile, ovvero che la derivata destra e la derivata sinistra debbano esistere ed essere uguali nel punto considerato. Se così non fosse la funzione non è derivabile. Si ricorda che la derivata destra e la derivata sinistra vengono espresse così come segue:
[math]f'(x_0)=\lim _{ h\rightarrow 0^+}{ \frac{f(x_0+h)-f(x_0)}{h} }[/math]
[math]f'(x_0)=\lim _{ h\rightarrow 0^-}{ \frac{f(x_0+h)-f(x_0)}{h} }[/math]
Affinché la funzione allora sia derivabile deve risultare che:
[math]f'(x_0)=\lim _{ h\rightarrow 0^+}{ \frac{f(x_0+h)-f(x_0)}{h} }=f'(x_0)=\lim _{ h\rightarrow 0^-}{ \frac{f(x_0+h)-f(x_0)}{h} }= P_O[/math]
Dove:
- [math]P_0[/math]è il valore che la derivata assume in quel punto
Osserva il pdf per un esempio per il calcolo e verifica della continuità di una funzione.
Scarica il file PDF
Per ulteriori approfondimenti sulla continuità, derivabilità ed esistenza del limite e calcolo delle derivate vedi qui
