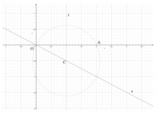
Determina i coefficienti a,b,c in modo che l'equazione
[math]ax^2 + by^2 - 2x + 6y + c = 0 [/math]
rappresenti la circonferenza passante per [math]O (0;0)[/math]
e [math]A(2;1)[/math]
e l'area del triangolo [math]OAC[/math]
, essendo [math]OC[/math]
un diametro.
Svolgimento
Sapendo che nell'equazione della
circonferenza i coefficienti delle due variabili di secondo grado sono uguali, possiamo scrivere:
[math]ax^2 + ay^2 - 2x + 6y + c = 0 [/math]
In questo modo avremmo solo due incognite.
Ora, sfruttiamo la condizione di appartenenza dei punti alla circonferenza, sostituendo le coordinate dei punti alle variabili dell'equazione:
[math] O ∈ C [/math]
[math]a \cdot 0^2 + a \cdot 0^2 - 2 \cdot 0 + 6 \cdot 0 + c = 0 [/math]
[math] c = 0 [/math]
[math] A ∈ C [/math]
[math]a \cdot 2^2 + a \cdot 1^2 - 2 \cdot 2 + 6 \cdot 1 + c = 0 [/math]
[math] 4a + a - 4 + 6 + c = 0 [/math]
[math] 5a + 2 + c = 0 [/math]
Impostiamo ora il sistema:
[math][/math]
left{ \begin{array}{rl}
c = 0 &\
3a + c + 2 = 0 &
end{array}\right.
[math][/math]
Sostituendo la prima equazione nella seconda:
[math] 3a + 0 + 2 = 0 \to a = - 2/5 [/math]
Abbiamo quindi che:
[math] a = b = - 2/5 , c = 0 [/math]
Scriviamo quindi l'equazione della circonferenza:
[math]- 2/5 x^2 - 2/5 y^2 - 2x + 6y + 0 = 0 [/math]
Trasformiamo l'equazione in modo che i coefficienti delle variabili di secondo grado siano 1:
[math]- 2 x^2 - 2 y^2 - 10 x + 30y = 0 [/math]
[math] x^2 + y^2 + 5 x - 15 y = 0 [/math]
Rappresentiamo la circonferenza sul piano cartesiano:
[math] C (-a/2 ; - b/2 ) \to C (-5/2 ; (15)/2 ) [/math]
[math] r = \sqrt{(-a/2)^2 + (-b/2)^2 - c } = \sqrt((-5/2)^2 + (-(-15)/2)^2 - 0 ) = [/math]
[math] \sqrt{ (25)/4 + (225)/4 } = \sqrt((250/4) = frac(5 \sqrt(10))(2) [/math]

Essendo
[math]OC[/math]
il diametro della circonferenza, esso varrà:
[math] d = 2r = 2 \cdot frac(5 \sqrt{10})(2) = 5 \sqrt{10} [/math]
Sappiamo poi che il triangolo
[math]OAC[/math]
, essendo inscritto in una semicirconferenza, è rettangolo; di conseguenza, per determinare la sua area basterà moltiplicare fra loro i due cateti e dividere per due.
Conoscendo le coordinate dei punto
[math]O[/math]
e
[math]A[/math]
, possiamo determinare la loro distanza:
[math]d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} [/math]
[math] OA = \sqrt{( 2 - 0 )^2 + ( 1 - 0 )^2} = \sqrt(4+1) = \sqrt5 [/math]
Ora, per trovare il cateto maggiore
[math]AC[/math]
possiamo utilizzare il teorema di
Pitagora:
[math]AC = \sqrt{OC^2 - AO^2} = \sqrt((5\sqrt(10))^2 - (\sqrt5)^2) = \sqrt(250-5) = 7\sqrt5 [/math]
Calcoliamo ora la sua area:
[math] A_(AOC) = frac(AO \cdot AC)(2) = frac(\sqrt5 \cdot 7\sqrt5){2} = (35)/2 [/math]