_francesca.ricci
di _francesca.ricci
(70 punti)
8' di lettura
Data l'equazione
[math] (2k - 1) x^2 + ky^2 + (1-k) y - 8k + 4 = 0[/math]
:
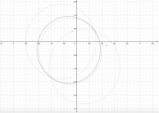
  1. determinare k in modo che essa rappresenti una circonferenza C ; disegnarla indicando con A e B i suoi punti di intersezione con l'asse x;
  2. determinare k in modo che essi rappresenti una parabola P , di vertice V, con asse parallelo all'asse y, tracciarne il grafico verificando che anch'essa passa per A e B;
  3. determinare gli altri due punti C e D comuni a C e P ;
  4. sull'arco CVD di P determinare un punto P tale che sia uguale a
    [math]13/4[/math]
    la somma delle sue distanze dall'asse y e dalla retta CD.

Risoluzione (1)

L'equazione di una circonferenza è del tipo
[math] x^2 + y^2 + ax + by + c = 0[/math]
; notiamo che i coefficienti delle incognite di secondo grado sono uguali e valgono (nel caso generale) 1.
Quindi, per prima cosa, imponiamo che:

[math] 2k - 1 = k[/math]

Risolviamo l'equazione e determiniamo k:

[math] 2k - 1 - k = 0 \to k - 1 = 0 \to k = 1[/math]

Sostituendo questo valore di k all'equazione parametrica otteniamo l'equazione della circonferenza C :

[math] (2 \cdot 1 - 1) x^2 + 1 \cdot y^2 + (1-1) y - 8 \cdot 1 + 4 = 0[/math]

[math] (2 - 1) x^2 + y^2 + 0 \cdot y - 8 + 4 = 0[/math]

[math] x^2 + y^2 - 4 = 0[/math]

Essendo i coefficienti dei termini di secondo grado uguali a 1 non sono necessari ulteriori passaggi.

Disegniamo la circonferenza, tenendo conto che il suo centro è situato in

[math] C (-a/2 ; - b/2) \to C(-0/2 ; -0/2) \to C(0 ; 0) [/math]

e che il suo raggio misura

[math] r = \sqrt{(-a/2)^2 + (-b/2)^2 - c} = \sqrt(0 + 0 - (-4)) = \sqrt(4) = 2 [/math]

Rappresentiamo la circonferenza:

Abbiamo quindi due punti di intersezione con l'asse x:

[math] A (-2 ; 0) , B (2 ; 0)[/math]

Risoluzione (2)

Per far in modo che l'equazione rappresenti una parabola, ricordiamo che con asse parallelo all'asse y ha un'equazione del tipo
[math] y = ax^2 + bx + c [/math]
; non compare quindi un termine y di secondo grado. Poniamo quindi il coefficiente di
[math]y^2[/math]
uguale a zero, quindi abbiamo k=0. Sostituiamo questo valore all'equazione parametrica:

[math] (2 \cdot 0 - 1) x^2 + 0 \cdot y^2 + (1-0) y - 8 \cdot 0 + 4 = 0[/math]

[math] - x^2 + y + 4 = 0[/math]

Ricaviamo la y e portiamo l'equazione in forma esplicita:

[math] y = x^2 - 4 [/math]

Per tracciare il grafico della parabola troviamo il suo vertice:

[math] V (0 ; c) \to V (0 ; -4) [/math]

Ora diamo dei valori arbitrari alla variabile indipendente, e determiniamo almeno due punti appartenenti alla parabola; per comodità determiniamo le intersezioni con gli assi cartesiani:

[math] P ∩ {x = 0} [/math]

[math][/math]
left{ \begin{array}{rl}
x =0 &\
y =x^2 - 4 &
end{array}\right.
[math][/math]

[math][/math]
left{ \begin{array}{rl}
x =0 &\
y =0^2 - 4 to y = -4 &
end{array}\right.
[math][/math]

[math]P ∩ {y = 0} [/math]

[math][/math]
left{ \begin{array}{rl}
y =0 &\
y =x^2 - 4 &
end{array}\right.
[math][/math]

[math][/math]
left{ \begin{array}{rl}
y =0 &\
0 =x^2 - 4 to x = ± 2 &
end{array}\right.
[math][/math]

Rappresentiamo quindi la parabola:

Verifichiamo che anche la parabola passa per A e B sostituendo le coordinate dei due punti alle variabili dell'equazione della parabola; se otteniamo un'identità i punti appartengono al luogo geometrico.

[math] A ∈ P \to 0 = (-2)^2 - 4 \to 0 = 4 - 4 \to 0 = 0[/math]

[math] B ∈ P \to 0 = (2)^2 - 4 \to 0 = 4 - 4 \to 0 = 0[/math]

I due punti appartengono alla parabola.

Risoluzione (3)

Per determinare glia altri due punti comuni alla parabola e alla circonferenza impostiamo un sistema fra le due equazioni:

[math][/math]
left{ \begin{array}{rl}
x^2 + y^2 - 4 =0 &\
y =x^2 - 4 &
end{array}\right.
[math][/math]

Risolviamo il sistema per sostituzione, sostituendo la y della seconda equazione all'incognita della prima:

[math][/math]
left{ \begin{array}{rl}
x^2 + (x^2 - 4)^2 - 4 =0 &\
y =x^2 - 4 &
end{array}\right.
[math][/math]

[math][/math]
left{ \begin{array}{rl}
x^2 + x^4 + 16 - 8x^2 - 4 =0 &\
y =x^2 - 4 &
end{array}\right.
[math][/math]

[math][/math]
left{ \begin{array}{rl}
x^4 - 7 x^2 + 12 =0 &\
y =x^2 - 4 &
end{array}\right.
[math][/math]

Dalla prima equazione troviamo

[math]x^2[/math]
mediante la formula
[math] x = frac(- b ± \sqrt{b^2 - 4ac})(2a) [/math]
:

[math] x^2 = frac(- (-7) ± \sqrt{(-7)^2 - 4 \cdot 12})(2) = frac(7 ± \sqrt(49 - 48))(2) = frac(7 ± 1)(2)[/math]

[math] x_1 ^2 = frac(7 + 1)(2) = 8/2 = 4 \to x_1 = ± \sqrt{4} = ± 2[/math]

Questo primo risultato corrisponde all'ascissa dei punti A e B trovati in precedenza;

[math] x_2 ^2 = frac(7 - 1)(2) = 6/2 = 3 \to x_2 = ± \sqrt{3} [/math]

Determiniamo ora le ordinate dei due punti:

[math][/math]
left{ \begin{array}{rl}
x = \sqrt{3} &\
y =(\sqrt{3})^2 - 4 to y = 3 - 4 = -1 &
end{array}\right.
[math][/math]

Abbiamo quindi il punto

[math] C ( \sqrt{3} ; -1 )[/math]

[math][/math]
left{ \begin{array}{rl}
x = - \sqrt{3} &\
y =(- \sqrt{3})^2 - 4 to y = 3 - 4 = -1 &
end{array}\right.
[math][/math]

Abbiamo quindi il punto

[math] D (- \sqrt{3} ; -1 )[/math]

Risoluzione (4)

Notiamo che esistono due punti P, simmetrici rispetto all'asse y, che hanno la proprietà richiesta dal problema. Prendiamo in considerazione il punto P', poiché esso ha ascissa positiva.

Sappiamo che questo punto appartiene alla parabola, di conseguenza possiamo scrivere le sue coordinate in questo modo:

[math] P (x , x^2 - 4)[/math]

La sua distanza dall'asse y

[math] P'H [/math]
, quindi, ci è già nota e corrisponde a x, l'ascissa del punto P:

[math] d _(P'H) = x[/math]

Dobbiamo ora trovare la distanza del punto P dalla retta CD.

Determiniamo l'equazione della retta CD, sapendo che essa è parallela all'asse x:

[math] CD : y = - 1 [/math]

Determiniamo la distanza del punto P dalla retta CD sottraendo all'ordinata di H' (ortogonale al punto P) l'ordinata del punto P stesso:

[math] d _(P'H') = - 1 - (x^2 - 4) = - 1 - x^2 + 4 = - x^2 + 3[/math]

Sapendo che

[math] d _(P'H') + d _(P'H) = frac(13)(4) [/math]
possiamo determinare il valore di x:

[math] - x^2 + 3 + x = frac(13)(4)[/math]

[math] - 4 x^2 + 12 + 4x = 13 \to - 4 x^2 + 12 + 4x + 13 = 0[/math]

[math] - 4 x^2 + 4x - 1 = 0 \to 4 x^2 - 4x + 1 = 0 [/math]

[math] (2x - 1)^2 = 0 \to x = 1/2 [/math]

Abbiamo quindi che

[math]P' ( 1/2 ; x^2 - 4) [/math]
; troviamo l'ordinata di P:

[math] y_P' = x^2 - 4 = (1/2)^2 - 4 = 1/4 - 4 = frac(1 - 16)(4) = - 15/4 [/math]

[math]P' ( 1/2 ; - (15)/4)[/math]

Il punto P, simmetrico di P' rispetto l'asse y, avrà la stessa ordinata di P', ma ascissa opposta:

[math]P ( 1/2 ; - (15)/4)[/math]
Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it