Studia il fascio di parabole di equazione:
[math] (m + 1) x^2 - 4(m + 1) x - (m + 1) y + 4 + 5m = 0[/math]
e determina poi:
- la parabola del fascio passante per il punto A(3;-3);
- la parabola del fascio che intercetta sull'asse delle ascisse un segmento di lunghezza 6;
- la parabola del fascio tangente alla retta
[math] 2x - y - 3 = 0 [/math]
Risoluzione (0)
Cominciamo studiando il fascio di parabole, cioè determinando le generatrici, gli eventuali punti base e le parabole degeneri.
Per determinare le parabole generatrici del fascio, scriviamo in forma implicita la sua equazione e raccogliamo rispetto al parametro m:
[math] m x^2 + x^2 - 4mx - 4 x - my - y + 4 + 5m = 0[/math]
[math] (x^2 - 4x - y + 5) m + x^2 - 4x - y + 4 = 0[/math]
Le equazioni delle due generatrici si ottengono una per m=0 e l'altra uguagliando a zero l'espressione che è moltiplicata per m:
[math] m = 0[/math]
[math] (x^2 - 4x - y + 5) \cdot 0 + x^2 - 4x - y + 4 = 0[/math]
[math] x^2 - 4x - y + 4 = 0 \to y = x^2 - 4x + 4[/math]
[math]x^2 - 4x - y + 5 = 0 \to y = x^2 - 4x + 5[/math]
Per trovare i punti base risolviamo il sistema delle equazioni delle due generatrici:
[math][/math]
left{ \begin{array}{rl}
y = x^2 - 4x + 4 &\
y = x^2 - 4x + 5&
end{array}\right.
[math][/math]
Risolviamo con il metodo del confronto:
[math]x^2 - 4x + 4 = x^2 - 4x + 5 \to 4 = 5[/math]
Abbiamo ottenuto una falsa identità, di conseguenza non abbiamo punti base.
Le parabole, quindi, potrebbero essere esterne oppure congruenti e con lo stesso asse.
Le parabole degeneri si ottengono uguagliando a zero il coefficiente di
[math]x^2[/math]
se dipende dal parametro, o uguagliando a zero il coefficiente di y.
In questo caso, i due coefficienti sono uguali:
[math] m + 1 = 0 \to m = -1[/math]
Sostituiamo questo valore all'equazione:
[math](- 1 + 1)^2 - 4(- 1 + 1) - (- 1 + 1) y + 4 + 5 \cdot (-1) = 0 [/math]
[math] 4 - 5 = 0[/math]
Poiché non abbiamo ottenuto un'equazione, possiamo affermare che non esistano parabole degeneri in questo fascio.
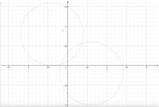
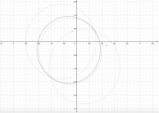
Ora, rappresentiamo nel piano cartesiano il fascio di parabole.
Per farlo dobbiamo individuare il suo asse; quindi, scriviamo l'equazione della parabola in forma esplicita e troviamo il suo vertice in funzione del parametro:
[math] (m + 1) y = (m + 1) x^2 - 4(m + 1) x + 4 + 5m [/math]
[math] y = frac((m + 1) x^2 - 4(m + 1) x + 4 + 5m)(m + 1) [/math]
[math] y = x^2 - 4x + frac(4 + 5m)(m + 1)[/math]
Possiamo affermare che la parabola ha l'asse parallelo all'asse delle ordinate, quindi il suo vertice sarà:
[math] V ( - b/(2a); - Δ/(4a)) [/math]
[math] x_V = - b/(2a) = - frac(-4)(2) = 2[/math]
Per semplificare i calcoli, possiamo trovare l'ordinata del vertice sostituendo l'ascissa all'equazione del fascio:
[math] y = 2^2 - 4 \cdot 2 + frac(4 + 5m)(m + 1) = 4 - 8 + frac(4 + 5m)(m + 1) =[/math]
[math] - 4 + frac(4 + 5m)(m + 1) = frac(- 4m - 4 + 4 + 5m)(m + 1) = frac(m)(m + 1)[/math]
[math] V ( 2 ; frac(m)(m + 1)) [/math]
Notiamo quindi che l'asse delle parabole è di equazione
[math] x = 2[/math]
.
Inoltre, poiché il coefficiente della x di secondo grado è 1, tutte le parabole del fascio sono con la concavità rivolta verso l'alto.
Rappresentiamo ora il fascio di parabole, dando dei valori arbitrari al parametro m.

Risoluzione (1)
Sapendo cha la parabola in questione passa per il punto A(3;-3), sostituiamo le coordinate di questo punto all'equazione del fascio per trovare il valore del parametro m:
[math] y = x^2 - 4x + frac(4 + 5m)(m + 1)[/math]
[math] -3 = 3^2 - 4 \cdot 3 + frac(4 + 5m)(m + 1)[/math]
[math] -3 = 9 - 12 + frac(4 + 5m)(m + 1) \to frac(4 + 5m)(m + 1) = 0 [/math]
[math] 4 + 5m = 0 \to m = - 4/5 [/math]
Sostituiamo ora questo valore del parametro m all'equazione del fascio, trovando così l'equazione della parabola richiesta.
[math] y = x^2 - 4x + frac(4 + 5 \cdot ( - 4/5))( - 4/5 + 1)[/math]
[math] y = x^2 - 4x + frac(4 - 4)( 1/5)[/math]
[math] y = x^2 - 4x [/math]
Risoluzione (2)
La parabola che stiamo cercando intercetta sull'asse delle ascisse un segmento di lunghezza 6, cioè interseca in due punti l'asse x e questi due punti distano 6.
Quindi, per prima cosa, determiniamo le intersezioni del fascio con l'asse x:
[math] F ∩ y = 0[/math]
[math] 0 = x^2 - 4x + frac(4 + 5 \cdot ( - 4/5))( - 4/5 + 1)[/math]
[math] x^2 - 4x + frac(4 + 5 \cdot ( - 4/5))( - 4/5 + 1) = 0 [/math]
Risolviamo con la formula ridotta
[math] x = frac(-b/2 ± \sqrt{(-b/2)^2 - ac})(a)[/math]
:
[math] x = frac(-(-4)/2 ± \sqrt{(-(-4)/2)^2 - frac(4 + 5m)(m + 1)})(1) = 2 ± \sqrt(4 - frac(4 + 5m)(m + 1)) =[/math]
[math] 2 ± \sqrt{frac(4m + 4 - 4 - 5m)(m + 1)} = 2 ± \sqrt(frac( - m)(m + 1))[/math]
Abbiamo due soluzioni:
[math] x_1 = 2 - \sqrt{frac( - m)(m + 1)} , x_2 = 2 + \sqrt{frac( - m)(m + 1)}[/math]
Sappiamo che la distanza fra
[math] x_1[/math]
e
[math]x_2[/math]
vale 6 e che
[math]x_2 > x_1[/math]
.
Per trovare la distanza fra due punti appartenenti alla stessa retta, sottraiamo l'ascissa del più piccolo a quella del più grande:
[math] d (x_1 ; x_2) = x_2 - x_1 = 2 + \sqrt{frac( - m)(m + 1)} - (2 - \sqrt{frac( - m)(m + 1)})[/math]
Poniamo questa distanza uguale a 6:
[math] 2 + \sqrt{frac( - m)(m + 1)} - (2 - \sqrt{frac( - m)(m + 1)} )= 6[/math]
Determiniamo le condizioni di esistenza, quindi poniamo il radicando maggiore o uguale a zero:
[math] frac( - m)(m + 1) ≥ 0[/math]
[math] N ≥ 0 \to - m ≥ 0 \to m ≤ 0[/math]
[math] D > 0 \to m + 1 > 0 \to m > -1[/math]

[math] 0 ≤ m
Risolviamo l'equazione e determiniamo il valore di m:
[math] 2 \sqrt{frac( - m)(m + 1)} = 6[/math]
[math]\sqrt{frac( - m)(m + 1)} = 3[/math]
[math] [\sqrt{frac( - m)(m + 1)}]^2 = 3^2[/math]
[math]frac( - m)(m + 1) = 9[/math]
[math] - m = 9m + 9 \to m = - 9/(10)[/math]
Sostituendo il valore ottenuto di m all'equazione del fascio troviamo l'equazione della parabola richiesta:
[math] y = x^2 - 4x + frac(4 + 5 \cdot (- 9/(10)))(- 9/(10) + 1)[/math]
[math] y = x^2 - 4x + frac(4 - 9/2)( 1/(10))[/math]
[math] y = x^2 - 4x + frac( - 1/2)( 1/(10))[/math]
[math] y = x^2 - 4x - 5[/math]
Risoluzione (3)
Determiniamo ora la parabola tangente alla retta
[math]2x - y - 3 = 0[/math]
. Sappiamo che la parabola e la retta hanno solo un punto in comune, quindi sappiamo che il sistema fra le equazioni del fascio e della retta avrà due soluzioni reali coincidenti.
Impostiamo quindi il sistema, dopo aver reso le due equazioni in forma esplicita:
[math][/math]
left{ \begin{array}{rl}
y = x^2 - 4x + frac{4 + 5m}{m + 1}&\
y = 2x - 3&
end{array}\right.
[math][/math]
Risolviamo il sistema con il metodo del confronto:
[math] x^2 - 4x + frac(4 + 5m)(m + 1) = 2x - 3[/math]
[math] x^2 - 4x + frac(4 + 5m)(m + 1) - 2x + 3 = 0[/math]
[math] x^2 - 6x + frac(4 + 5m)(m + 1) + 3 = 0[/math]
[math] x^2 - 6x + frac(4 + 5m + 3m + 1)(m + 1) = 0[/math]
[math] x^2 - 6x + frac(8m + 7)(m + 1) = 0[/math]
Risolviamo con la formula ridotta
[math] x = frac(-b/2 ± \sqrt{(-b/2)^2 - ac})(a)[/math]
:
[math] x = frac(-(-6)/2 ± \sqrt{(-(-6)/2)^2 - frac(4 + 5m)(m + 1)})(1) = 3 ± \sqrt(9 - frac(7 + 8m)(m + 1)) =[/math]
[math] 3 ± \sqrt{frac(9m + 9 - 7 - 8m)(m + 1)} = 3 ± \sqrt( frac(m + 2)(m + 1)) [/math]
Sapendo che l'equazione deve avere due soluzioni reali coincidenti, poniamo
[math]Δ = 0[/math]
:
[math] frac(m + 2)(m + 1) = 0 \to m + 2 = 0 \to m = -2[/math]
Sostituendo il valore ottenuto di m all'equazione del fascio troviamo l'equazione della parabola richiesta:
[math] y = x^2 - 4x + frac(4 + 5 \cdot (- 2))(- 2 + 1)[/math]
[math] y = x^2 - 4x + frac(4 - 10)(-1)[/math]
[math] y = x^2 - 4x + frac(-6)(-1)[/math]
[math] y = x^2 - 4x + 6[/math]



![Geometria analitica: Determinare il valore del parametro m per il quale la retta di equazione [math]{y}=\frac{{{2}-{m}}}{{2}}{x}+\frac{1}{{2}}{\left(\frac{1}{{m}}-{1}\right)}{m}\ne{0}[/math]](https://cdn.skuola.net/shared/thumb/159x141/news_foto/2008/09/geom_anal_e15-1.jpg)