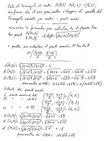_francesca.ricci
di _francesca.ricci
(70 punti)
3' di lettura
Dato il triangolo
[math]ABC[/math]
e un punto
[math]O[/math]
esterno ad esso, siano
[math]A’[/math]
,
[math]B’[/math]
,
[math]C’[/math]
rispettivamente i simmetrici di
[math]A[/math]
,
[math]B[/math]
,
[math]C[/math]
rispetto a
[math]O[/math]
.

Dimostra che i triangoli

[math]ABC[/math]
e
[math]A’B’C’[/math]
sono congruenti.
congruenza_triangoli

Svolgimento

Consideriamo i triangoli
[math]BCO[/math]
e
[math]B’C’O[/math]
; essi hanno:
  • [math]BO = B’O[/math]
    per ipotesi (in quanto
    [math]O[/math]
    è il centro di simmetria);
  • [math]\hat{BOC} = \hat{B’OC’}[/math]
    perché angoli opposti al vertice;
  • [math]CO = C’O[/math]
    per ipotesi (in quanto
    [math]O[/math]
    è il centro di simmetria);
Quindi, per il primo criterio di congruenza dei triangoli, avendo due lati e l’angolo fra essi compreso congruente, i triangoli
[math]BCO[/math]
e
[math]B’C’O[/math]
sono congruenti.

Da ciò si deduce che

[math]BC = B’C’[/math]
perché lati opposti ad angoli congruenti.Ora consideriamo i triangoli
[math]ABO[/math]
e
[math]A’B’O[/math]
.
Essi hanno:
  • [math]AO = A’O[/math]
    per ipotesi (in quanto
    [math]O[/math]
    è il centro di simmetria);
  • [math]\hat{AOB} = \hat{A’OB’}[/math]
    perché angoli opposti al vertice;
  • [math]BO = B’O[/math]
    per ipotesi (in quanto
    [math]O[/math]
    è il centro di simmetria);
Quindi, per il primo criterio di congruenza dei triangoli, avendo due lati e l’angolo fra essi compreso congruente, i triangoli
[math]ABO[/math]
e
[math]A’B’O[/math]
sono congruenti.

Segue che

[math]AB = A’B’[/math]
perché lati opposti ad angoli congruenti.Ora consideriamo i triangoli
[math]ACO[/math]
e
[math]A’C’O[/math]
. Essi hanno:
  • [math]AO = A’O[/math]
    per ipotesi (in quanto O è il centro di simmetria);
  • [math]\hat{AOC} = \hat{A’OC’}[/math]
    perché angoli opposti al vertice;
  • [math]CO = C’O[/math]
    per ipotesi (in quanto
    [math]O[/math]
    è il centro di simmetria);
Quindi, per il primo criterio di congruenza dei triangoli, avendo due lati e l’angolo fra essi compreso congruente, i triangoli
[math]ACO[/math]
e
[math]A’C’O[/math]
sono congruenti.

Possiamo dedurre quindi che

[math]AC = A’C’[/math]
.

Di conseguenza, i triangoli

[math]ABC[/math]
e
[math]A’B’C’[/math]
sono congruenti per il terzo criterio di congruenza dei triangoli, avendo tre lati congruenti.
Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it