Risoluzione
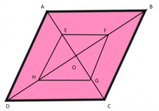
Sappiamo che in ogni parallelogramma le diagonali si tagliano a metà; possiamo allora affermare che:
[math] \bar{AO} ≅ \bar{OC} [/math]
[math] \bar{DO} ≅ \bar{OB} [/math]
Inoltre, sappiamo per ipotesi che:
[math] \bar{AB} ≅ \bar{BC} ≅ \bar{CD} ≅ \bar{DA} [/math]
Consideriamo ora i quattro triangoli che si formano dalle diagonali:
[math]ABO[/math]
, [math]BOC[/math]
, [math]COD[/math]
, [math]DOA[/math]
.Ciascuno di essi ha un lato che è il lato del parallelogramma, e due lati in comune con altri due triangoli, cosicché tutti hanno tre lati congruenti agli altri tre triangoli.
Quindi, per il terzo criterio di congruenza dei triangoli, essi sono tutti e quattro congruenti.
Possiamo quindi affermare che gli angoli
[math]Ahat OB[/math]
, [math]Bhat OC[/math]
, [math]Chat OD[/math]
, [math]Dhat OA[/math]
.sono congruenti.
Poiché essi sono angoli che formano un angolo giro (360°), e sono quattro, ciascuno di essi misurerà 90°.
Le diagonali del parallelogramma sono quindi perpendicolari.