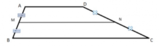
Risoluzione
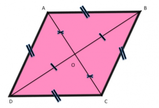
Per dimostrare che il quadrilatero EFGH è un parallelogramma, dobbiamo dimostrare che due suoi lati opposti siano congruenti e paralleli.Consideriamo i triangoli AOB e DOC. Sapendo che in un parallelogramma i lati opposti sono congruenti e che le diagonali si tagliano a metà, possiamo affermare che :
Di conseguenza, per il terzo criterio di congruenza dei triangoli, AOB e DOC sono congruenti.
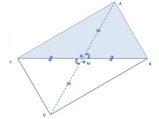
Consideriamo ora il triangolo HOG: sappiamo che i suoi lati sono la metà dei lati del triangolo DOC, e che con esso vi è un angolo in comune, HOG.
Quindi, per il secondo criterio di similitudine dei triangoli, avendo un angolo congruente e i lati che lo comprendono in proporzione, essi sono simili.
Per le stesse ragioni, possiamo affermare che AOB è simile ad EOF.
Ma, poiché AOB = DOC, sarà che HOG è simile a EOF.Ma dato che sappiamo che i loro vertici cono situati nei punti medi delle diagonali del parallelogramma, possiamo affermare che
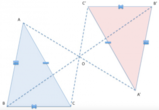
Quindi, i triangoli HOG e EOF sono congruenti per il primo criterio di congruenza dei triangoli, avendo due lati congruenti e l’angolo fra essi compreso (opposto al vertice) congruente.
Di conseguenza, anche gli angoli EFO è simile a OHG, opposti a lati congruenti, saranno congruenti.
Per questo motivo, possiamo affermare che essi sono angoli alterni interni, generati da due parallele (EF e HG) tagliate da una trasversale (HF).
Due lati del quadrilatero EFGH sono quindi paralleli; con un ragionamento analogo si dimostra che anche gli altri due lati sono paralleli fra loro. Il quadrilatero è quindi un parallelogramma.