_francesca.ricci
di _francesca.ricci
(70 punti)
1' di lettura
Nel piano cartesiano disegna i punti
[math]A(1,1)[/math]
,
[math]B(5,0)[/math]
,
[math]C(4,3)[/math]
. Costruisci il simmetrico
[math]A'B'C'[/math]
del triangolo
[math]ABC[/math]
rispetto all'asse delle
[math]y[/math]
. Dimostra che
[math]ABC=A'B'C'[/math]
.

Risoluzione

Disegniamo il triangolo
[math]ABC[/math]
:

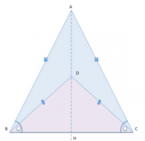
[caption id="attachment_16328" align="alignnone" width="350"]triangoli_e_simmetria Triangolo

[math]ABC[/math]
.

E ora il suo simmetrico rispetto all'asse delle y:

[caption id="attachment_16329" align="alignnone" width="350"]triangoli_e_simmetria Triangolo

[math]ABC[/math]
e suo simmetrico
[math]A'B'C'[/math]
.

La simmetria rispetto all'asse y è una simmetria assiale, cioè la trasformazione che fa corrispondere ad ogni punto del piano il suo simmetrico rispetto una asse.

La simmetria assiale è un'isometria.

Sappiamo quindi che la distanza tra due punti della figura di partenza è uguale alla distanza delle loro immagini, con la simmetria assiale, cioè, non vengono modificate le distanze.

Sappiamo quindi che i triangoli in figura hanno i tre lati congruenti; possiamo affermare quindi, per il terzo criterio di congruenza dei triangoli, che essi sono congruenti.

Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it