In una semicirconferenza di diametro AB è inscritto il trapezio isoscele ABCD il cui lato AD è metà della base maggiore AB. Determinare il perimetro e l'area del trapezio sapendo che è verificata la seguente relazione:
[math]2/7 ar{AB} +2/3 ar{AD}=36cm[/math]
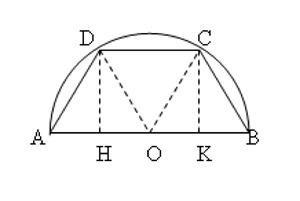
Pongo
[math]ar{AB}=x[/math]
si ha
[math]ar{AD}=1/2 x[/math]
Sostituendo nella relazione data si ha
[math]2/7 x + 2/3 \cdot 1/2 x =2,6
2/7 x +1/3 x =2,6[/math]
[math]
6x+7x=54,6m.c.m.=21
[/math]
[math]
x=frac{54,6}{13} = 4,2cm[/math]
[math]
ar{AB}=4,2cm[/math]
[math]
ar{AD}=2,1cm[/math]
[math]
l=2,1cmAOD è un triangolo equilatero di la o [/math]
[math]
ar{DH}=l/2 sqrt(3) = frac{2,1}{2}*sqrt(3)=1,81cm[/math]
[math]
AH=l/2 = frac{2,1}{2}=1,05[/math]
[math]
DC=AB-2AH=2l-2*l/2=l=2,1cm[/math]
[math]
2p(ABCD)=5*2,1cm=10,5cm[/math]
[math]
A(ABCD)=frac{(4,2+2,1)*1,82}{2}=5,72cm^2[/math]
[math] [/p[/math]
