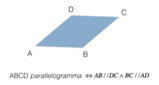
In questi appunti troverai un esercizio svolto attraverso l'impiego del teorema di
Pitagora e dei criteri di similitudine dei triangoli riguardante i rombi
Traccia dell'esercizio sui rombi con calcolo del perimetro e dell'area
In un rombo
[math]ABCD[/math]
ciascun lato misura
[math]12cm[/math]
e l'angolo in
[math]B[/math]
ha ampiezza
[math]120°[/math]
. Prendere sui lati
[math]\bar{AB}[/math]
,
[math]\bar{BC}[/math]
,
[math]\bar{CD}[/math]
e
[math]\bar{AD}[/math]
del rombo rispettivamente i punti
[math]P[/math]
,
[math]Q[/math]
,
[math]S[/math]
e
[math]T[/math]
in modo che i segmenti
[math]\bar{AP}[/math]
,
[math]\bar{BQ}[/math]
,
[math]\bar{CS}[/math]
e
[math]\bar{DT}[/math]
misurino
[math]2cm[/math]
ciascuno, calcolare il perimetro e l'area del quadrilatero
[math]PQST[/math]
, dopo aver dimostrato che esso è un parallelogramma.

Come dimostrare che una figura sia un quadrilatero
Per prima cosa, dimostriamo che il quadrilatero
[math]PQST[/math]
è un parallelogramma; per farlo, dobbiamo dimostrare che abbia I lati opposti congruenti.
Analizziamo i dati che abbiamo:
[math]\bar{AB}=\bar{BC}=\bar{CD}=\bar{DA} = 12 cm [/math]
perché sono tutti lati di un rombo.
[math]\bar{AP}=\bar{BQ}=\bar{CS}=\bar{DT} = 2 cm [/math]
come indicato dalla traccia.
Possiamo ricavare quindi, per differenza, le misure dei segmenti :
[math]\bar{PB}=\bar{QC}=\bar{SD}=\bar{TA} = 12 cm - 2 cm = 10 cm [/math]
Inoltre possiamo affermare che
[math] \hat{B}=\hat{D}[/math]
perché sono angoli opposti di un rombo e in particolare
[math] hat{B}= hat{D} = 120°[/math]
. Infine,
[math] \hat{A}=\hat{C}[/math]
perché angoli opposti di un rombo;
Prendiamo in considerazione I triangoli
[math]PBQ[/math]
e
[math]SDT[/math]
. Essi hanno:
[math] \bar{PB}=\bar{SD} = 10 cm[/math]
[math] \bar{BQ}=\bar{DT} = 2 cm[/math]
[math] \hat{B}= \hat{D} = 120° cm[/math]
Avendo due lati e l'angolo fra essi compreso congruenti, I triangoli
[math]PBQ[/math]
e
[math]SDT[/math]
sono congruenti per il
primo criterio di congruenza dei triangoli.
Di conseguenza,
[math] \bar{PQ}=\bar{ST} [/math]
, poiché sono
lati opposti a angoli congruenti.
Abbiamo dimostrato, quindi, che due lati opposti del quadrilatero
[math]PQST[/math]
sono congruenti. Con un procedimento analogo, considerando i triangoli
[math]APT[/math]
e
[math]QCS[/math]
, si dimostra che anche
gli altri due lati opposti sono congruenti. Queste informazioni sono sufficienti per affermare che
il quadrilatero in questione è un parallelogramma.
Come determinare il perimetro del parallelogramma
Per determinare il perimetro del parallelogramma, cerchiamo per prima cosa di determinare la
lunghezza del lato [math]\bar{PT}[/math]
. Tracciamo da
[math]T[/math]
la
perpendicolare al lato
[math] \bar{AB}[/math]
del
rombo.
Consideriamo i triangoli
[math]AOD[/math]
e
[math]AKT[/math]
.

Essi hanno:
Quindi, per il
primo criterio di similitudine dei triangoli [math]AOD[/math]
e
[math]AKT[/math]
sono simili.
Possiamo affermare, quindi, che i loro lati sono in proporzione:
[math] \bar{TA} : \bar{AD} = \bar{TK} : \bar{AO}[/math]
[math] 10 cm : 12 cm = \bar{TK} : \bar{AO}[/math]
Sapendo che l'angolo
[math]\hat{B}[/math]
misura
[math]120°[/math]
e che l'angolo
[math]\hat{A}[/math]
ne misura
[math]60°[/math]
, possiamo affermare che il
triangolo [math]ABD[/math]
è
equilatero, poiché ha gli angoli di
[math]60°[/math]
. Avendo il suo lato, possiamo ricavare la sua
altezza, cioè il segmento
[math] \bar{AO}[/math]
:
[math]\bar{AO} = \sqrt{\bar{AB}^2 - \bar{BO}^2} = \sqrt{\bar{AB}^2 - (\frac{\bar{AB}}{2})^2} =[/math]
[math] \sqrt{ 12^2 - (\frac{12}{2})^2} = \sqrt(144 - 36) = \sqrt(108) [/math]
che possiamo scrivere come
[math] 6 \sqrt3 [/math]
. Quindi:
[math] 10 cm : 12 cm = \bar{TK} : 6 \sqrt3 cm [/math]
[math] \bar{TK} = \frac{6 \sqrt3 \cdot 10}{12} = 5 \sqrt3 cm [/math]
Poiché il triangolo
[math]AKT[/math]
è
rettangolo e sappiamo che
[math] \bar{TK} = 5 \sqrt3 cm[/math]
e
[math] \bar{TA} = 10 cm [/math]
, con il
teorema di Pitagora possiamo determinare la
lunghezza del cateto [math] \bar{AK}[/math]
:
[math]\bar{AK} = \sqrt{\bar{AT}^2 - \bar{TK}^2} = \sqrt(10^2 - (5 \sqrt3)^2) =[/math]
[math] \sqrt{100 - 75} = \sqrt(25) = 5 [/math]
Possiamo trovare la lunghezza del segmento
[math]\bar{PK} [/math]
:
[math]\bar{PK} = \bar{AK} - \bar{AP} = 5 cm - 2 cm = 3 cm [/math]
Poiché anche il triangolo
[math]TPK[/math]
è
rettangolo e sappiamo che
[math]\bar{TK} = 5 \sqrt3 cm [/math]
e
[math]\bar{PK} = 3 cm [/math]
, con il
teorema di Pitagora possiamo determinare la
lunghezza del lato[math]\bar{TP} [/math]
:
[math]\bar{TP} = \sqrt{\bar{TK}^2 + \bar{PK}^2} = \sqrt((5 \sqrt3)^2 + 3^2) =[/math]
[math] \sqrt{ 75 + 9} = \sqrt(84) = 2 \sqrt(21) [/math]
Per trovare la lunghezza dell'altra coppia di lati del parallelogramma, dobbiamo seguire un procedimento analogo tracciando da
[math]P[/math]
la perpendicolare al lato
[math]\bar{BC}[/math]
del
rombo:
Consideriamo il triangolo
[math]PHB[/math]
. Sapendo che l'angolo
[math]\hat{B}[/math]
misura
[math]120°[/math]
, possiamo affermare che l'angolo
[math]\hat{PBH}[/math]
misura
[math]60°[/math]
, poiché insieme all'angolo
[math]\hat{B}[/math]
forma un
angolo piatto. Di conseguenza, il
triangolo [math]PHB[/math]
è simile al triangolo
[math]AOD[/math]
.

Essi hanno:
Quindi, per il
primo criterio di similitudine dei triangoli,
[math]AOD[/math]
e
[math]AKT[/math]
sono simili.
Possiamo affermare, quindi, che i loro lati sono in proporzione:
[math] \bar{TA} : \bar{AD} = \bar{TK} : \bar{AO}[/math]
[math] 10 cm : 12 cm = \bar{TK} : \bar{AO}[/math]
Possiamo quindi mettere i loro lati in proporzione:
[math] \bar{PB} : \bar{AD} = \bar{PH} : \bar{AO}[/math]
[math] 10 cm :12 cm= \bar{TK} : 6 \sqrt3 cm[/math]
[math] \bar{PH} = \frac{6\sqrt3 \cdot 10}{12} = 5 \sqrt3 cm [/math]
Determiniamo ora la lunghezza del segmento
[math] \bar{HB}[/math]
con il
teorema di Pitagora, sapendo che il triangolo
[math]PHB[/math]
è
rettangolo:
[math]\bar{HB} = \sqrt{\bar{PB}^2 - \bar{PH}^2} = \sqrt(10^2 - (5 \sqrt3)^2) =[/math]
[math] \sqrt{100 - 75} = \sqrt(25) = 5 [/math]
Troviamo ora la lunghezza del segmento
[math]\bar{HQ}[/math]
:
[math]\bar{HQ} = \bar{QB} + \bar{HB} = 2 cm + 5 cm = 7 cm [/math]
Determiniamo ora la lunghezza del lato
[math] \bar{PQ}[/math]
con il
teorema di Pitagora, sapendo che il triangolo
[math]PHQ[/math]
è
rettangolo:
[math]\bar{PQ} = \sqrt{\bar{PH}^2 + \bar{QH}^2} = \sqrt((5 \sqrt3)^2 + 7^2) =[/math]
[math] \sqrt{75 + 49} = \sqrt(124) = 2\sqrt(31) [/math]
Calcoliamo quindi il perimetro del parallelogramma
[math]PQST[/math]
:
[math] P_(PQST) = \bar{ST} + \bar{TP} + \bar{PQ} + \bar{QS} = [/math]
[math] 2 \bar{TP} + 2 \bar{PQ} = 2 \cdot 2 \sqrt{21} + 2 \cdot 2 \sqrt(31) = [/math]
[math] 4 (\sqrt{21} + \sqrt(31)) cm [/math]
Come determinare l'area del parallelogramma partendo dall'altezza e dalla base dei triangoli
Per determinare l'
area del parallelogramma, procediamo determinando prima l'
area del rombo e poi sottraendogli l'
area dei triangoli [math]SDT[/math]
,
[math]TAP[/math]
,
[math]PBQ[/math]
e
[math]QSC[/math]
.
[math] A_(ABCD) =D \cdot d = 2 \cdot \bar{AO} \cdot \bar{DB} = [/math]
[math] 2 \cdot 6 \sqrt3 \cdot 12 = 144 \sqrt3 cm^2 [/math]
Determiniamo l'area del triangolo
[math]PBQ[/math]
, congruente a
[math]SDT[/math]
.
La sua altezza, che cade fuori dal triangolo, è il segmento
[math]\bar{PH}[/math]
, mentre la sua
base è
[math]\bar{QB} [/math]
. La sua
area sarà quindi:
[math] A_(PBQ) = A_(SDT) = frac(\bar{QB} \cdot \bar{PH})(2) = frac(2 \cdot 5 \sqrt3){2} = 5 \sqrt3 cm^2[/math]
Calcoliamo ora l'area del triangolo
[math]APT[/math]
, congruente a
[math]QSC[/math]
.
La sua altezza, che cade anch'essa fuori dal triangolo, è il segmento
[math]\bar{TK}[/math]
, mentre la sua
base è
[math]\bar{AP}[/math]
. La sua
area sarà quindi:
[math] A_(APT) = A_(QSC) = \frac{\bar{AP} \cdot \bar{TK}}{2} = \frac{2 \cdot 5 \sqrt3}{2} = 5 \sqrt3 cm^2[/math]
Troviamo ora l'area del parallelogramma:
[math] A_(PQST) = A_(ABCD) - [ A_(PBQ) + A_(SDT) + A_(APT) + A_(QSC) ] = [/math]
[math] 144 \sqrt3 cm^2 - [5 \sqrt3 + 5 \sqrt3 + 5 \sqrt3 + 5 \sqrt3] cm^2 = [/math]
[math] (144 \sqrt3 - 20 \sqrt3) cm^2 = 124 \sqrt3 cm^2 [/math]
Per ulteriori approfondimenti sul calcolo dell'area dei parallelogrammi vedi anche qui

 Essi hanno:
Essi hanno: