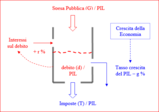
Lo Stato, qui inteso come Amministrazione Pubblica, ha un suo bilancio annuale costituto da entrate (contributi e tributi) ed uscite (spese e investimenti). Il bilancio annuale entrate-uscite può essere positivo (surplus) oppurei, molto più spesso, negativo (deficit). La somma algebrica dei surplus e deficit accumulati negli anni passati costituisce la parte sostanziale del Debito dello Stato (in seguito Debito). Il Debito è costituito in grandissima parte da Titoli di Stato, emessi e rinnovati periodicamente dal Ministero del Tesoro. I Titoli di Stato costituiscono un prestito richiesto dall'Amministrazione Pubblica per far fronte ai suoi impegni economici e finanziari. I titoli vengono acquistati da privati e società (Fondi, Banche, Assicurazioni). Per convincere gli investitori a comprare e tenere i Titoli di Stato, lo Stato deve pagare un interesse. La somma di tutti gli interessi pagati ogni anno dallo Stato si definisce Servizio del Debito (attualmente pari a circa 70 miliardi di € in Italia). Per coprire il deficit annuale lo Stato emette nuovi Titoli di ammontare pari al deficit. In tal modo aumenta il Debito.
IL DEBITO
Il Debito rappresenta la somma dei debiti contratti dalle varie parti dell'amministrazione pubblica: Amministrazione Centrale, Regioni, Provincie, Comuni,…L'argomento debito, come sappiamo, è ampiamente dibattuto. Un recente libro dell'economista Carlo Cottarelli "Il macigno. Perché il debito pubblico ci schiaccia e come si fa a liberarsene" fa il punto e ci spiega con chiarezza la natura del problema ed i possibili rimedi. E' un libro di dimensione limitata (circa 150 pagine) molto scorrevole e di facile lettura.
L'Italia fa parte dell'Unione Europea (EU) e dell'Eurozona (insieme dei Paesi dell'EU che usano l'Euro come valuta) ed è tenuta a rispettare diversi Trattati, in particolare il Trattato di Maastricht e, recentemente, il Fiscal Compact. Questi Trattati stabiliscono dei limiti massimi al Deficit (prima 3% del PIL, in futuro 0,5%) ed al Debito (60% del PIL). L'Italia, sotto il controllo attento dell'EU ha iniziato un percorso virtuoso di rientro nei limiti del Deficit. Si trova tuttavia in difficoltà a rientrare nei limiti del Debito. Il Fiscal Compact è un trattato firmato dall'Italia e dagli altri Paesi dell'Eurozona ed inserito nella Costituzione. Dunque tutti questi Paesi si sono assunti un impegno serio e vincolante.
Questo articolo si vuole dedicare allo studio di come soddisfare i limiti del debito richiesti dal Fiscal Compact, mettendo in luce le variabili, i parametri, le equazioni e provando a simulare le dinamiche.
Ricordiamo, ad esempio, che secondo Eurostat, il debito italiano ammontava a fine 2015 a 2172 miliardi €, mentre il PIL era pari a 1642 miliardi € e dunque il rapporto valeva 132.7%, valore che ci pone al penultimo gradino della classifica all'interno della EU, ben lontano dagli altri Paesi.
Ora l'obbligo richiesto dal Fiscal Compact ha generato discussioni infinite in Italia, coinvolgendo opinionisti e politici. Diversi hanno dichiarato o scritto che l'Italia dovrebbe rimborsare ogni anno decine di miliardi di € del suo Debito, cosa che appare realizzabile solo a fronte di notevoli sacrifici (nuove pesantissime tasse).
Gli economisti, poco ascoltati, hanno fatto presente che questa interpretazione del Fiscal Compact è sbagliata: il FC non ci richiede di ridurre il debito in 20 anni. Ed anche, a dire il vero, nessuno ci richiede necessariamente di ridurre il debito. Ci si richiede di ridurre il rapporto debito/PIL. Questo può essere fatto aumentando il PIL, che e il denominatore. Per far questo l'economia deve crescere notevolmente.
Lo stesso argomento vale per diversi Paesi europei che, come noi, hanno superato ampiamente il limite del 60%. Vediamo come erano messi in termini di debito i più grandi Paesi europei:
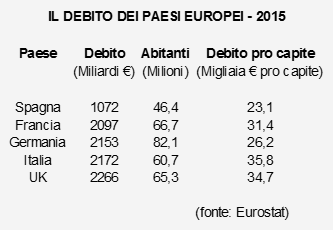
Si vede che in termini di debito l'Italia si pone allo stesso livello di Francia, Germania, UK. Un confronto più preciso, in valori pro-capite, mostra che L'Italia è allo stesso livello di UK e non molto superiore alla Francia.
In termini di debito/PIL l'Italia è messa molto peggio, anche se tutti questi Paesi eccedono il 60%, come riportato nella tabella sotto (escludiamo UK dalla classifica perché non fa parte dell'Eurozona e quindi non è tenuta al vincolo del Fiscal Compact).
| Paese | (d_{2015}/Y_{2015}) |
|---|---|
| Spagna | 99,2% |
| Francia | 95,8% |
| Germania | 71,2% |
| Italia | 132,7% |
Per far questo proviamo ad applicare l'equazione ((\ref{eq10})), sviluppata dagli economisti, che è stata dimostrata nell' APPENDICE 2, dove il rapporto debito/PIL dell'anno i (Big(frac{d_i}{Y_i}Big) ) è uguale al rapporto debito/PIL dell'anno precedente corretto per il fattore
[ frac{d_i}{Y_i} = (1+r-g) frac{d_{i-1}}{Y_{i-1}} + frac{DP_i}{Y_i} ]
Facciamo qui l'ipotesi che il termine (frac{DP_i}{Y_i}), vale a dire la percentuale di disavanzo annuo, si possa considerare costante nel ventennio futuro (2016-2035). E quindi:
[ frac{d_i}{Y_i} = (1+r-g) frac{d_{i-1}}{Y_{i-1}} + frac{DP}{Y} ]
E' questa una equazione alle differenze finite di 1° grado che si risolve come riportato in APPENDICE 3.
E si ottiene, nel caso generale in cui (r
e g):
[ frac{d_n}{Y_n} = frac{frac{DP}{Y}}{g-r} + Big( frac{d_0}{Y_0}-frac{frac{DP}{Y}}{g-r}Big)(1+r-g)^n ]
Dove (frac{DP}{Y}) è il rapporto tra il disavanzo ed il PIL, assunto costante per tutto il periodo
Risolvendo rispetto a (frac{DP}{Y} ) si ottiene:
[ frac{DP}{Y} = -(r-g)frac{frac{d_n}{Y_n}-frac{d_0}{Y_0}(1+r-g)^n}{1-(1+r-g)^n} ]
Nel caso speciale in cui risulta
[ frac{d_n}{Y_n} = frac{DP}{Y} n + frac{d_0}{Y_0}(1+r-g)^n ]
Che risolta rispetto a (frac{DP}{Y}) diventa:
[ frac{DP}{Y} = frac{frac{d_n}{Y_n}-frac{d_0}{Y_0}(1+r-g)^n}{n} ]
Nella pratica si preferisce usare l'Avanzo Primario (AP) invece del disavanzo primario. Ed è chiaramente:
[ AP = -DP ]
Nel nostro caso abbiamo
Il termine (frac{d_0}{Y_0}) si riferisce all'anno 2015 ed è diverso secondo il Paese considerato.
Sostituendo l'Avanzo Primario al posto del Disavanzo Primario le due equazioni diventano:
[\begin{equation} frac{AP}{Y}=(r-g)frac{frac{d_n}{Y_n}-frac{d_0}{Y_0}(1+r-g)^n}{1-(1+r-g)^n} ,,,,,,,,, r
e g label{eq1} end{equation} ]
[\begin{equation} frac{AP}{Y}=-frac{frac{d_n}{Y_n}-frac{d_0}{Y_0}(1+r-g)^n}{n} ,,,,,,,,, r =g label{eq2} end{equation} ]
Le due equazioni così sviluppate correlano tra loro i due parametri
Ora il parametro
Il governo di ogni Stato può far qualcosa, ma non molto, per ridurre il tasso d'interesse, qualcosa in più per stimolare la crescita nominale dell'economia (aumentare g): in definitiva per ridurre il parametro
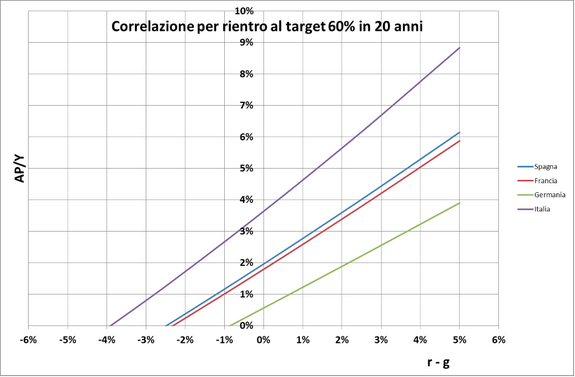
Osserviamo che in pratica i valori realistici che possiamo aspettarci per il parametro
Nel diagramma seguente si riporta l'andamento di (d/Y) per l'Italia nell'ipotesi di mantenere costanti nel periodo 2016-2035 i valori dei due parametri: (r-g=0,, , ,, frac{AP}{Y} = 3.6\%)
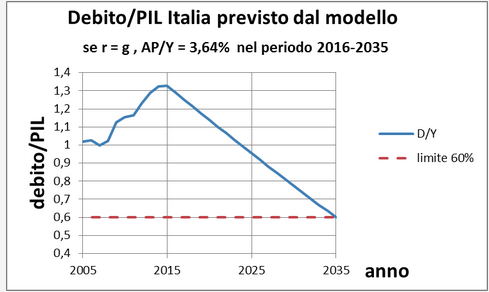
E' realistico tutto questo?
Vediamo sotto la Tabella delle serie storica di (frac{AP}{Y}) per i Paesi in esame:
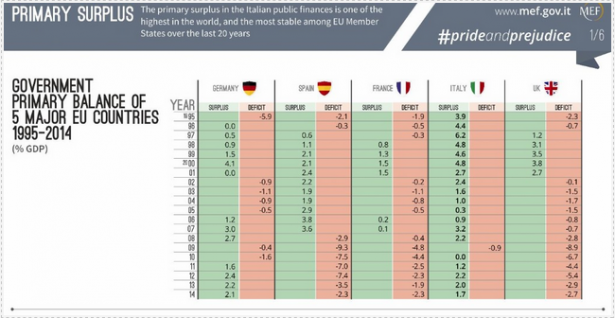
Si vede chiaramente che nel corso della crisi (iniziata dal 2008) tutti i Paesi hanno avuto un Avanzo Primario negativo, tranne Germania e Italia.
Per quanto la situazione dell'Europa stia migliorando, la crisi economica non è ancora terminata. In questa condizione non appare molto credibile che i Paesi considerati (tranne la Germania) possano acquisire a breve i valori di (frac{AP}{Y}) necessari per soddisfare il vincolo del 60%. Se e quando la crisi sarà completamente superata, si può immaginare che i Paesi avranno modo di migliorare l'Avanzo Primario. Ma è ben difficile che (frac{AP}{Y}) possa mantenere valori elevati e costanti per i prossimi 20 anni, in particolare per l'Italia.
Quanto al parametro
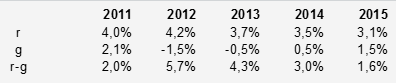
Si nota un'importante riduzione di
È comunque evidente che in Italia una riduzione importante del debito ridurrebbe notevolmente il servizio del debito. Le somme risparmiate potrebbero essere usate dallo Stato per lo sviluppo del Paese.
In alternativa potrebbe essere utile bloccare il debito (numeratore) ai valori attuali e far crescere il PIL (denominatore).
Anche l'inflazione gioca un ruolo non trascurabile: un aumento dell'inflazione produrrebbe un aumento del PIL nominale, riducendo in tal modo il rapporto debito/PIL. Anche per questo motivo la BCE (Banca Centrale Europea) da alcuni anni attua, attraverso massicci acquisti di Titoli di Stato, una decisa politica finanziaria per portare l'inflazione dai valori attuali (prossimi allo zero) al target del 2%.
Molti economisti e politici ritengono che per far uscire i Paesi dalla crisi siano necessarie misure economiche di tipo keynesiano, come una robusta dose di investimenti pubblici (ad es. nel settore delle infrastrutture, che farebbero da volano allo sviluppo di importanti settori produttivi). Per far questo si dovrebbe aumentare la spesa pubblica (termine G nell'equazione del PIL) operando in ampio deficit di bilancio, cosa non ammessa dai Trattati.
E' opinione di molti che i vincoli su deficit e debito imposti dai Trattati, ragionevoli in epoca di economia stabile, siano troppo restrittivi nei periodi di crisi. E che, pertanto, i Paesi in particolare difficoltà dovrebbero allearsi per ottenere che tali vincoli siano rinegoziati e opportunamente ammorbiditi.
Tutti i calcoli dell'articolo sono riportati nel file EXCEL allegato.
CONCLUSIONI
L'articolo ha presentato un'analisi relativa al modo in cui i Paesi dell'Eurozona potrebbero attuare una manovra di rientro entro il vincolo del 60% per il rapporto debito/PIL richiesto dai Trattati. Per far questo si è fatto ricorso a una formula ben nota agli economisti, abbinata dall'autore a noti metodi matematici per la soluzione delle equazioni alle differenze. Ne è scaturito un semplice modello di prima approssimazione che ha permesso di fare delle considerazioni significative.Naturalmente, come non è difficile immaginare, la realtà è più complessa. Il lettore interessato all'argomento può trovare un'analisi formale della gestione del debito in un manuale del Fondo Monetario Internazionale (IMF) riportato nei riferimenti.
APPENDICE 1 - IL PIL
Come detto in PREMESSA il PIL misura la produzione dell'intera economia del Paese. Come si determina il PIL? In diversi modi. Il più intuitivo e più usato è come spesa: somma dei contributi dei quattro settori dell'economia. Per convenzione si indica con[ \begin{equation} Y_i = C_i + I_i + G_i + XN_i label{eq3} end{equation} ]
dove:
(C_i=mbox{consumi (privati)})
(I_i=mbox{investimenti delle aziende} )
( G_i=mbox{spesa pubblica (acquisti e servizi)} )
( XN_i=mbox{esportazioni nette(esportazioni meno importazioni)} )
Il termine
Ad esempio il PIL dell'Italia nel 2015 era così costituito:
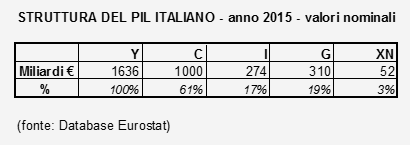
Come abbiamo visto il PIL si misura come valore (nell'Eurozona in Euro).
Ognuno dei quattro addendi del PIL si ottiene come somma dei prodotti dei prezzi per le rispettive quantità:
[ \sum_k p_{ik} q_{ik} ,,,,,, (i = mbox{anno}, k = mbox{prodotto})]
Ora noi sappiamo che i prezzi variano di anno in anno a causa dell'inflazione. Se dunque calcoliamo il PIL a prezzi correnti, otteniamo il PIL nominale. Di conseguenza anno dopo anno il PIL nominale varia perché sono variate sia le quantità che i prezzi. E' dunque teoricamente possibile che il PIL nominale cresca nel tempo per effetto dell'inflazione mentre le quantità non sono variate.
Esiste allora una seconda e diversa definizione del PIL che fa riferimento a prezzi costanti. In questo caso le somme si costruiscono in questo modo:
[ \sum_k p_{0k} q_{ik}]
Dove (p_{0k}) sta a indicare il prezzo del prodotto
Il PIL così costruito si definisce PIL reale, perché le variazioni che avvengono di anno in anno sono dovute solo alla variazione delle quantità prodotte. La misura corretta della crescita dell'economia è, ovviamente, il PIL reale. Le tabelle Eurostat che si possono consultare fanno riferimento ai prezzi dell'anno 2010. Le previsioni sulle variazione del PIL, che appaiono spesso sulla stampa, riguardano il PIL reale.
Mentre gli obblighi derivanti dai Trattati Europei sono basati sul rapporto Debito/PIL dove PIL e Debito sono nominali.
Ricordiamo infine che il PIL reale di un Paese misura la sua potenza economica, mentre il rapporto PIL/ore-lavorate misura la produttività.
APPENDICE 2 - LA FORMULA DI VARIAZIONE DEL RAPPORTO DEBITO/PIL NEL TEMPO
Quest'argomento è trattato dai testi di macroeconomia. Qui riportiamo come si ricava la formula perché è un bell'esempio di ragionamento logico-matematico. Tutte le grandezze qui utilizzate sono da intendersi a valori nominali.Come si è visto sopra, il Disavanzo (deficit nel linguaggio comune) dell'anno i è dato da:
[\begin{equation} D_i = rd_{i-1} + G_i - T_i label{eq4} end{equation} ]
Dove
(D_i =mbox{Disavanzo})
(G_i=mbox{Spesa dello Stato})
(T_i=mbox{tassazione netta (tasse meno trasferimenti)})
(r=mbox{tasso di interesse medio sul Debito})
(d_{i-1} =mbox{debito dell…²anno precedente})
Il termine (G_i-T_i) rappresenta dunque il bilancio dello stato come differenza uscite ed entrate. Esso è denominato Disavanzo Primario. Per comodità lo denominiamo (DP_i).
[ \begin{equation} DP_i equiv G_i - T_i label{eq5} end{equation} ]
Il termine (rd_{i-1}) è il Servizio del debito, vale a dire l'interesse pagato sul debito. L'equazione ((\ref{eq4})) ci dice che, sommando al Disavanzo primario il pagamento dell'interesse sul debito dell'anno precedente, si ottiene il disavanzo dell'anno in corso.
Sappiamo, inoltre, che con buona approssimazione si può considerare il disavanzo come differenza tra il debito dell'anno corrente e quello del precedente:
[ \begin{equation} d_i -d_{i-1} cong D_i label{eq6} end{equation} ]
Combinando le ((\ref{eq4})), ((\ref{eq5})), ((\ref{eq6})) si ha:
[ d_i = (1+r)d_{i-1} + DP_i ]
Ora dividiamo per il PIL dell'anno corrente:
[ frac{d_i}{Y_i} = (1+r) frac{d_{i-1}}{Y_i} + frac{DP_i}{Y_i} ]
Ora moltiplichiamo e dividiamo il primo addendo del secondo membro per il PIL dell'anno precedente:
[ \begin{equation} frac{d_i}{Y_i} = (1+r)frac{Y_{i-1}}{Y_i}cdot frac{d_{i-1}}{Y_{i-1}} + frac{DP_i}{Y_i} label{eq7} end{equation} ]
Infine introduciamo il tasso di crescita nominale del PIL:
[ g = frac{Y_i}{Y_{i-1}}-1 ]
Dalla quale risulta: [ frac{Y_{i-1}}{Y_i} = frac{1}{g+1} ]
Che introdotta nella ((\ref{eq7})) la modifica:
[ \begin{equation} frac{d_i}{Y_i} = frac{(1+r)}{(1+g)} cdot frac{d_{i-1}}{Y_{i-1}}+frac{DP_i}{Y_i} label{eq8} end{equation} ]
Il termine (frac{(1+r)}{(1+g)}) è complesso e vogliamo provare a semplificarlo. Per questo consideriamo che esso sia funzione della variabile g. Facciamo uno sviluppo in serie di McLaurin di tale funzione, considerando i primi due termini della formula:
[ f(g) = frac{(1+r)}{(1+g)}=f(0)+f'(0)g ]
Dove (f(0)=1+r) mentre: (f'(g)= - frac{(1+r)}{(1+g)^2} ) e dunque (f'(0)=−(1+r))
In definitiva:
[ \begin{equation} f(g) = (1+r) - (1+r)g = 1+r-g-rg label{eq9}end{equation} ]
Ora ragioniamo sugli ordini di grandezza degli addendi della ((\ref{eq9})): sappiamo che
[ frac{(1+r)}{(1+g)} cong 1+r-g ]
Che sostituiamo nella ((\ref{eq8})):
[ \begin{equation} frac{d_i}{Y_i} = (1+r-g) frac{d_{i-1}}{Y_{i-1}} + frac{DP_i}{Y_i} label{eq10} end{equation} ]
Questa formula verrà usata nell'articolo (sopra) per calcolare al rientro nei limiti del 60%,
APPENDICE 3 - RISOLUZIONE DELL'EQUAZIONE ALLE DIFFERENZE FINITE
L'equazione alle differenze finite lineare del 1° ordine è data da:[ \begin{equation} y_{n+1} + ay_n = b label{eq11} end{equation} ]
Dove a, b, c sono costanti assegnate.
Questo tipo di equazione è simile alle equazione differenziale lineare a coefficienti costanti.
Si risolve determinando la soluzione dell'equazione omogenea associata:
[ y_{n+1} + ay_n = 0 ]
E aggiungendo una soluzione particolare della equazione completa.
La soluzione dell'omogenea vale:
[ y_{n, mbox{omog}} = K(-a)^n ]
Mentre un integrale particolare dell'equazione completa vale:
[ y_{n,mbox{part}} = frac{b}{1+a} ]
quando
[ a
e -1 ]
[ y_{n,mbox{part}} = bn ]
quando
[ a = -1 ]
In definitiva la soluzione completa della ((\ref{eq11})) è data da:
[ \begin{equation} y_n = K(-a)^n + frac{b}{1+a},,,, mbox{quando } a
e -1label{eq12} end{equation} ]
[ \begin{equation} y_n = K(-a)^n + bn ,,,, mbox{quando } a = -1 label{eq13} end{equation} ]
La costante
RIFERIMENTI
- http://ec.europa.eu/eurostat/ (statistiche economia e bilancio pubblico dei Paesi EU)
- Blanchard, Amighini, Giavazzi - Scoprire la macroeconomia. Un passo in più - Il Mulino Manuali (formula del debito)
- John B. Taylor- Principles of Macroeconomics - Houghton Mifflin (PIL e sua struttura)
- http://www.mef.gov.it/inevidenza/article_0045.html (Serie storica Avanzo Primario 5 Paesi EU)
- http://www.dima.unige.it/~astengo/smid/analisi3/appunti_analisi3_equadiff.pdf (equazioni alle differenze)
- https://www.imf.org/external/pubs/ft/tnm/2010/tnm1002.pdf (Manuale IMF, con la trattazione analitica del debito e del suo controllo)