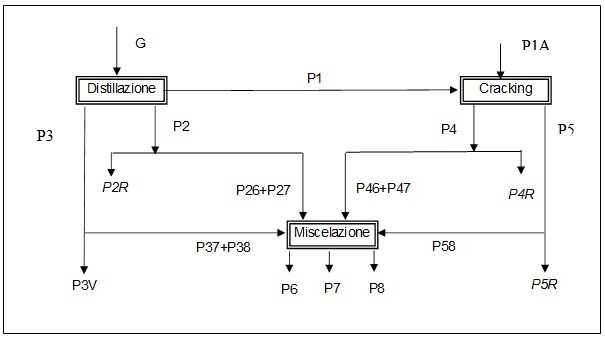
Il problema esposto rientra nell'ampio gruppo dei problemi di "composizione", "miscelazione" e "assemblaggio" nel gruppo cioè dei problemi di ricerca di una combinazione, avente determinate proprietà, partendo da componenti con caratteristiche note.
I problemi di composizione trovano pratica applicazione nell'industria in tutti i casi nei quali, attraverso approvvigionamento e trasformazioni di materie prime, si vogliano ottenere prodotti o semi lavorati a costo (o ad efficacia o ad una qualunque altra variabile significativa) ottimale. Esempi classici dei problemi di composizione sono quelli della dieta di minimo costo, garantendo tutti i necessari componenti nutrizionali, per collettività di uomini od animali, delle cariche dei forni metallurgici, dei cementifici, delle miscelazioni chimiche, farmaceutiche, alimentari, petrolifere ecc.Gli impianti di una raffineria consentono tre lavorazioni principali: 1) Distillazione frazionata, 2) Cracking, 3) Miscelazione, aventi le seguenti caratteristiche:
Distillazione del greggio. Dal greggio trattato si ottengono tre gruppi di prodotti :
- P1, in ragione di 0.4 kg per kg di greggio trattato; non utilizzabile direttamente, può essere solo avviato all'impianto di Cracking;
- P2, in ragione di 0.35 kg per kg di greggio trattato, può essere solo miscelato per formare altri prodotti;
- P3, in ragione di 0.25 kg per kg di greggio trattato; può essere miscelato con altri prodotti o venduto direttamente con un utile di 8 L/Kg.
- P4, in ragione di 0.6 kg per kg di P1 trattato;
- P5 in ragione di 0.4 kg per kg di prodotto trattato, entrambi destinati alla miscelazione.
- P6, composto da 0.5 di P2, 0.5 di P4, vendibile con un utile di 11 L/Kg.;
- P7, composto da 0.3 di P2, 0.3 di P4, vendibile con un utile di 10 L/Kg;
- P8, composto da 0.6 di P3, 0.4 di P5, vendibile con un utile di 14 L/Kg.
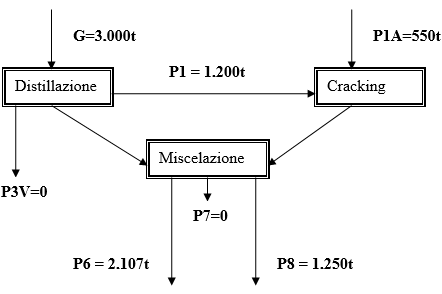
In un determinato momento, la raffineria dispone di una partita di 3,000 t. di greggio (G) ed ha la possibilità di acquistare direttamente sul mercato qualsiasi quantitativo di P1 (P1A) a costi identici di quelli risultanti all'uscita del suo impianto di distillazione. Supponendo che non vi siano vincoli di quantitativo minimo trattabile negli impianti si deve ricercare il programma di lavorazione e vendite cui corrisponde il massimo utile.
Otteniamo quindi un sistema di 21 variabili (riepilogate nello schema riportato sopra), collegate dalle 16 equazioni appresso riportate:
Distillazione:
1) P1 - 0.40*G = 0
2) P2 - 0.35*G = 0
3) P3 - 0.25*G = 0
Cracking:
4) P4 - 0.6*(P1A + P1) = 0
5) P5 - 0.4*(P1A + P1) = 0
Miscelazione:
6) P3V + P37 + P38 - P3 = 0
7) P26 + P27 + P2R - P2 = 0
8) P46 + P47 + P4R - P4 = 0
9) P58 + P5R - P5 = 0
10) P26 - 0.5*P6 = 0
11) P46 - 0.5*P6 = 0
12) P27 - 0.3*P7 = 0
13) P37 - 0.3*P7 = 0
14) P47 - 0.4*P7 = 0
15) P38 - 0.6*P8 = 0
16) P58 - 0.4*P8 = 0
Abbiamo 21-16 = 5 gradi di libertà per ottimizzare la produzione e le vendite dunque, rispettando questi vincoli, la funzione obiettivo (profitto) che ci interessa massimizzare è:
Z = 8*P3V + 11*P6 + 10*P7 + 14*P8
Naturalmente tutte le variabili debbono essere maggiori o uguali a zero e G =
Il problema è evidentemente di programmazione lineare e può essere agevolmente risolto con il metodo del simplesso ideato da Dantzig nel 1947. Negli anni 70 anche questi problemi, semplificati e di natura didattica, potevano essere risolti solo manualmente con una calcolatrice e molta esperienza/pazienza, oppure dai pochi che avevano accesso ai grandi mainframe, gli unici computer disponibili all'epoca. Con il programma MPSX della IBM il problema proposto fu risolto in 16 secondi di calcolo (elapsed time); oggi un moderno Personal Computer, per lo stesso problema, impiega circa 1.6 secondi, cioè è quasi 10 volte più veloce di un mainframe degli anni 70.
Di seguito sono riportati i valori di tutte le variabili che l'algoritmo del simplesso ha trovato evolvendo da un vertice all'altro del poliedro a 21 dimensioni, mantenendo sempre a zero tutti i vincoli di bilancio, sino al raggiungimento della soluzione ottimale:
| G= | 3000 |
| P1= | 1200 |
| P2= | 1050 |
| P3= | 750 |
| P4= | 1050 |
| P5= | 700 |
| P6= | 2100 |
| P7= | 0 |
| P8= | 1250 |
| P1A= | 550 |
| P3V= | 0 |
| P37= | 0 |
| P38= | 750 |
| P26= | 1050 |
| P27= | 0 |
| P2R= | 0 |
| P46= | 1050 |
| P47= | 0 |
| P4R= | 0 |
| P58= | 500 |
| P5R= | 200 |
La funzione obiettivo Z, con questi valori delle variabili che la massimizzano nel rispetto di tutti i vincoli, vale:
Max Z = 8 * 0 + 11 * 2100 + 10 * 0 + 14 * 1250 = 23,100 + 17,500 = 40.6 milioni di lire.
Si osservi che, in questo caso (ma non sempre e così perché bisogna anche tener conto delle quantità e dei costi delle risorse che i vari prodotti richiedono), il risultato trovato è in pieno accordo con il buon senso. L'algoritmo del Simplesso ha infatti scartato i prodotti più poveri: P3V (8 L/kg) e P7 (10 L/kg), promuovendo invece la produzione e vendita dei prodotti più redditizi P6(11L/Kg) e P8(14L/Kg).
Ricerca sulle conseguenze della riduzione degli utili su alcuni prodotti (What if? Analysis 1):
Si supponga ora che gli utili sul prodotto venduto P3V scenda da 8 a 7 L/kg ed inoltre che l'utile sul prodotto P8 scenda da 14 a 13 L/Kg.
La riduzione di guadagno sul prodotto P3V non ha alcuna influenza sul programma di produzione/vendita e sul valore ottimale della funzione obiettivo. Non era conveniente produrlo ad 8 L/Kg ed a maggior ragione non è conveniente produrlo a 7 Lit/Kg.
Anche la riduzione dell'utile sul prodotto P8 non implica variazioni sul programma di produzione che resta immutato. Cambia però il valore della funzione obiettivo che si riduce di 1.25 milioni di lire:
Max Z = 8 * 0 + 11 * 2100 + 10 * 0 + 13 * 1250 = 23,100 + 16,250 = 39.35 milioni di lire.
Ricerca sulle conseguenze di un limite massimo sull'acquisto di P1 (What if? Analysis 2):
Ci si chiede ora come il programma originario debba essere modificato qualora il quantitativo massimo di P1 acquistabile sul mercato esterno (P1A) sia limitato a 200t.
Come era da attendersi dalle precedenti ricerche, è conveniente distillare tutta la partita di greggio disponibile (G =
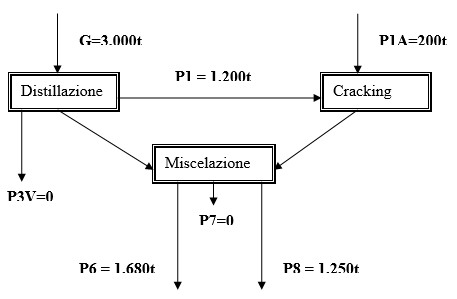
Max Z = 8 * 0 + 11 * 1680 + 10 * 0 + 14 * 1250 = 18,480 + 17,500 = 35.98 milioni di lire.
(Scarica il file File Excel relativo a questo problema)
Riferimenti
- U. DE SIMONI, R. CHIAPPI, La decisione motivata, (Non pubblicato), Ivrea 1976.
- F. HILLIER, G. LIEBERMAN, Introduction to Operations Research, Holden Day, San Francisco 1969.