francesco.speciale
di francesco.speciale
(50 punti)
2' di lettura

Nel quadrato

[math]ABCD[/math]
di lato
[math]l[/math]
, prolunghiamo i lati
[math]ar{AB}[/math]
dalla parte di
[math]B[/math]
e
[math]ar{AD}[/math]
dalla parte
di
[math]D[/math]
rispettivamente dei segmenti
[math]ar{BP=2x}[/math]
e
[math]ar{DQ}=3x[/math]
. Determina
[math]x[/math]
in modo tale che sia:
[math]2BD^2-2CQ^2=PQ^2-4CP^2[/math]

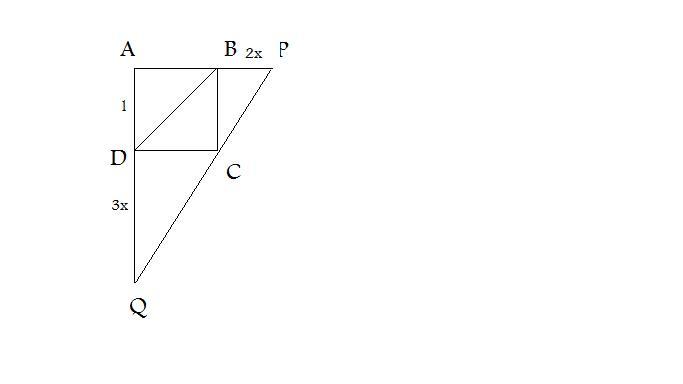
quadrato.jpg

Dati

[math]ar{BP=2x}[/math]

[math]ar{DQ}=3x[/math]

Svolgimento

[math]BD^2=2l^2[/math]

[math]CQ^2=l^2+9x^2[/math]

[math]CP^2=l^2+4x^2[/math]

[math]PQ^2=(l+2x)^2+(l+3x)^2=l^2+4x^2+4lx+l^2+9x^2+6x^2=2l^2+10lx+13x^2[/math]

Quindi l'equazione

[math]2BD^2-2CQ^2=PQ^2-4CP^2[/math]
, la possiamo riscrivere nel seguente modo:
[math]2(2l^2)-2(l^2+9x^2)=2l^2+10lx+13x^2-4(l^2+4x^2)[/math]
.
Risolviamo ora l'equazione
[math]2(2l^2)-2(l^2+9x^2)=2l^2+10lx+13x^2-4(l^2+4x^2)[/math]
;
[math]4l^2-2l^2-18x^2=2l^2+10xl+13x^2-4l^2-16x^2[/math]
;
Raccogliamo i termini simili
[math](-18-13+16)x^2-10lx+(4-2-2+4)l^2=0[/math]

[math]-15x^2-10lx+4l^2=0[/math]
, cioè
[math]15x^2+10lx-4l^2=0[/math]

[math](Delta)/4=(b/2)^2-ac=(5l)^2-(15 \cdot (-4l^2))=25l^2+60l^2=85l^2[/math]

[math]x_(1,2)=(-b/2+-\sqrt{(Delta)/4})/a=(-5l+-\sqrt(85l^2))/(15)=(-5l+-l\sqrt(85))/(15) => x_1=(l(+l\sqrt(85)-5))/(15) ^^ x_2=(l(-5-l\sqrt(85))/(15)[/math]
.

La soluzione

[math]x_2=(l(-5-l\sqrt{85})/(15)[/math]
non è accettabile perchè negativa.
Pertanto la soluzione del problema sarà:
[math]x=(l(+l\sqrt{85}-5))/(15)[/math]
.
Vuoi approfondire Algebra – Esercizi e Appunti di Algebra con un insegnante esperto?
Trovalo su Ripetizioni.it