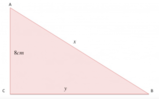
[math]2 cm[/math]
l'altezza, mentre ciascuno dei due lati congruenti supera di [math]2 cm[/math]
la base. Trova il perimetro e l'area del triangolo.

Svolgimento
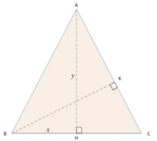
Chiamiamo con le incognite[math]x[/math]
ed [math]y[/math]
l'altezza del triangolo e metà base:
[math]AH = x [/math]
[math]HB = y[/math]
Sappiamo che:
[math]AB = HC + 2 cm[/math]
[math]AC = BC = AB + 2 cm[/math]
Troviamo la misura dei lati congruenti in funzione delle incognite:
[math] AC = BC = \sqrt{CH^2 + HB^2} = \sqrt(x^2 + y^2) [/math]
Possiamo ora impostare un sistema:
[math][/math]
left{ \begin{array}{rl}
2y = x + 2 &\
sqrt{x^2 + y^2} = 2y + 2 &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
2y = x + 2 &\
sqrt{x^2 + y^2} = 2y + 2 &
end{array}\right.
[math][/math]
Ricaviamo un'incognita dalla prima equazione e risolviamo il sistema per sostituzione:
[math][/math]
left{ \begin{array}{rl}
y = frac{x + 2}{2} &\
sqrt{x^2 + y^2} = 2y + 2 &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
y = frac{x + 2}{2} &\
sqrt{x^2 + y^2} = 2y + 2 &
end{array}\right.
[math][/math]
Lavoriamo sulla seconda equazione:
[math]\sqrt{x^2 + (frac(x + 2)(2))^2} = 2 \cdot frac(x + 2)(2) + 2 [/math]
[math]\sqrt{x^2 + frac(x^2 + 4 + 4x)(4)} = x + 2 + 2 [/math]
[math]\sqrt{frac(4 x^2 + x^2 + 4 + 4x)(4)} = x + 4 [/math]
[math]\sqrt{frac(5 x^2 + 4 + 4x)(4)} = x + 4 [/math]
Sapendo che
[math]x[/math]
deve essere positivo, perché è la misura di un lato, non è necessario porre le condizioni di esistenza.
[math](\sqrt{frac(5 x^2 + 4 + 4x)(4)} )^2 = (x + 4)^2 [/math]
[math]frac(5 x^2 + 4 + 4x)(4) = x^2 + 16 + 8x [/math]
[math] 5 x^2 + 4 + 4x = 4x^2 + 64 + 32x [/math]
[math] 5 x^2 + 4 + 4x - 4x^2 - 64 - 32x = 0 [/math]
[math] x^2 - 28x - 60 = 0 [/math]
Risolviamo con la formula ridotta
[math] x = frac(-b/2 ± \sqrt{(b/2)^2 - ac})(a) [/math]
[math] x = frac(-(-28)/2 ± \sqrt{((-28)/2)^2 - (-60)})(1) = 14 ± \sqrt(196 + 60) = [/math]
[math] 14 ± \sqrt{256} = 14 ± 16 [/math]
Accettiamo solo la radice positiva, quindi
[math]x=30[/math]
.Ricaviamo il corrispondente valore di y:
[math] y = frac(30 + 2)(2) = 16 [/math]
Determiniamo l'area del triangolo:
[math] A = frac(AB \cdot CH)(2) = frac(32 \cdot 30)(2) = 480 cm^2 [/math]
Troviamo la lunghezza del lato obliquo:
[math]AC = BC = \sqrt{CH^2 + HB^2} = \sqrt(x^2 + y^2) = \sqrt(30^2 + 16^2 ) = [/math]
[math] \sqrt{900 + 256} = \sqrt(1156) = 34 cm [/math]
Possiamo quindi calcolare il perimetro del triangolo:
[math] P = AB + 2 BC = 32 + 2 \cdot 34 = 100 cm [/math]