Nel parallelogramma ABCD della figura, il lato AB misura 10m e l'altezza DH ad esso relativa è lunga 4m. Calcola la misura dell'altezza relativa al lato BC sapendo che esso è lungo 8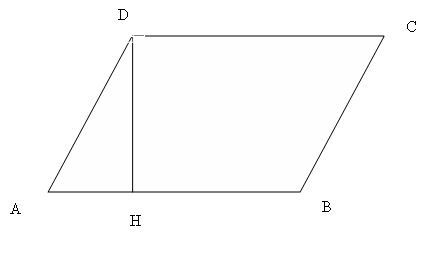 m.
m.
[math]AB=10m[/math]
[math]DH=4m[/math]
[math]BC=8m[/math]
[math]DK=......[/math]
Per calcolare la misura di
[math]DB[/math]
si deve prima calcolare l'area del parallelogrammo. Per calcolarla possiamo prendere o come base
[math]AB[/math]
e la relativa altezza o
[math]BC[/math]
e la relativa altezza.
Dovendo calcolare l'altezza relativa a
[math]BC[/math]
prendiamo in considerazione
[math]AB[/math]
come base.
[math]A=ABxxDH=10xx4=40[/math]
A questo punto possiamo calcolre la misura di
[math]DB[/math]
:
[math]DK=A:BC=40:8=5[/math]
Si può riunire tutto in un unica formula:
[math]DB=ABxxDH:CB=10xx4:8=40:8=5[/math]
[math]DB=5m[/math]
 m.
m.