_stan
di _stan
(320 punti)
4' di lettura
La funzione in questione è una funzione trigonometrica fratta, quindi dobbiamo escludere dal dominio i valori di x che annullano i denominatori:

[math] \\sin (x) = 0 \to x = kπ , k in Z [/math]

[math] \\cos(x) = 0 \to x = π/2 + kπ , k in Z [/math]

Quindi, il dominio della funzione é

[math] D = R - { kπ ; π/2 + kπ} , k in Z [/math]
.

Determiniamo ora i punti di intersezione con gli assi:

[math] f(x) _|_ (x = 0) [/math]

La funzione non presenta punti di intersezione con l'asse y, in quanto il valore

[math]x = 0[/math]
è escluso dal dominio.

[math] f(x) _|_ (y = 0) [/math]

[math] f(x) = 0 \to frac(1)(\\sin x) + frac(1)(\\cosx) = 0 [/math]

[math] frac(1)(\\sin x) = - frac(1)(\\cosx) \to \\cos(x) = - \\sin(x) [/math]

[math] x = -π/4 + 2kπ V x = 3/4 π + 2kπ \to x = -π/4 + kπ [/math]

Otteniamo i punti

[math] ( x = -π/4 + 2kπ ; 0 ) [/math]
.

Verifichiamo se la funzione è pari o dispari:

[math] f(-x) = frac(1)(\\sin (-x)) + frac(1)(\\cos(-x)) = frac(1)(- \\sin(x)) + frac(1)(\\cos(x)) [/math]

La funzione quindi non è ne pari ne dispari.

Cerchiamo i punti in cui la funzione è positiva:

[math] f(x) > 0 \to frac(1)(\\sin (x)) + frac(1)(\\cos(x)) > 0[/math]

[math] frac(\\cos(x) + \\sin (x))(\\sin(x) \\cos(x)) > 0 [/math]

[math] \\cos(x) + \\sin (x) > 0 \to -π/4 + 2kπ
[math]\\sin (x) \\cos(x) > 0 \to 0 + kπ

Dallo studio del segno si ottengono i seguenti intervalli:

[math] 2kπ

[math] uu 3/2π + 2kπ

In tali intervalli la funzione è crescente.

Passiamo ora alla ricerca degli asintoti; dobbiamo quindi determinare i limiti della funzione.

In questo caso, essendo lai funzione periodica, non ha senso calcolare i limiti a

[math]\pm oo[/math]
. Dato che la funzione non è definita in
[math] x = kπ[/math]
e
[math] x = π/2 + kπ[/math]
, calcoliamo i limiti per x che tende a tali punti, che potrebbero rappresentare degli asintoti verticali:

[math] lim_(x \to kπ) frac(1)(\\sin x) + frac(1)(\\cosx) = oo [/math]

Quindi le rette di equazione

[math] x = kπ[/math]
rappresentano asintoti verticali per la funzione; allo stesso modo:

[math] lim_(x \to π/2 + kπ) frac(1)(\\sin x) + frac(1)(\\cosx) = oo [/math]

Quindi anche le rette di equazione

[math] x = π/2 + kπ[/math]
rappresentano asintoti verticali per la funzione.

Studiamo ora il comportamento della derivata prima della funzione:

[math] f'(x) = - frac(\\cosx)(\\sin ^2(x)) + frac(\\sin(x))(\\cos^2(x)) = frac(\\sin^3(x) - \\cos^3(x))( \\sin^2(x) \\cos^2(x)) [/math]

Troviamo i punti in cui la deriva prima si annulla:

[math] f'(x) = 0 \to frac(\\sin ^3(x) - \\cos^3(x))( \\sin^2(x) \\cos^2(x)) = 0 [/math]

[math] \\sin ^3(x) - \\cos^3(x) = 0 \to \\sin ^3(x) = \\cos^3(x) [/math]

[math] \\sin (x) = \\cos(x) \to x = π/4 + kπ [/math]

Studiamo il segno della derivata prima:

[math] f'(x) > 0 \to frac(\\sin ^3(x) - \\cos^3(x))( \\sin^2(x) \\cos^2(x)) > 0 [/math]

[math] \\sin ^3(x) - \\cos^3(x) > 0 [/math]

[math] \\sin ^2(x) \\cos^2(x) > 0 [/math]

Dallo studio del segno si ottengono i seguenti intervallo:

[math] ( π/4 + 2kπ , 5/4 π + 2kπ ) [/math]

ciò significa che la funzione è crescente in tali intervalli. Di conseguenza, possiamo affermare che in corrispondenza dei punti

[math] x = π/4 + 2kπ [/math]
la funzione presente dei minimi relativi, mentre in corrispondenza dei punti
[math] x = 5/4π + 2kπ [/math]
la funzione presente dei massimi relativi.

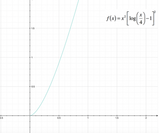
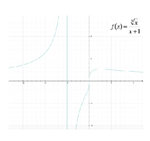
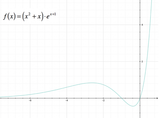
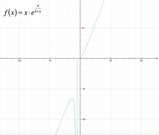
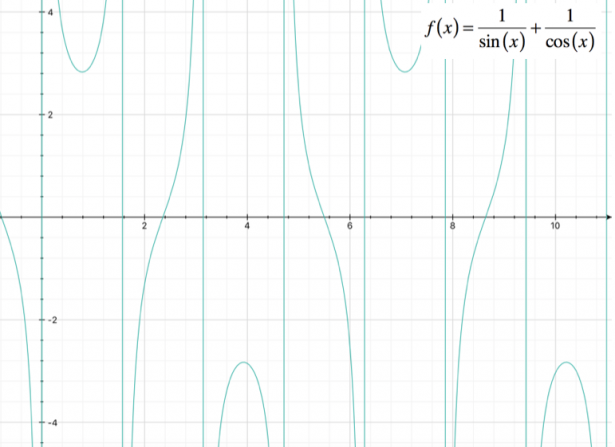
Possiamo procedere rappresentando il grafico approssimativo della funzione:

Potrebbe interessarti anche

Vuoi approfondire Algebra – Esercizi e Appunti di Algebra con un insegnante esperto?
Trovalo su Ripetizioni.it