Nel caso di funzioni esponenziali, sappiamo che il dominio corrisponde a tutto l'insieme dei
numeri reali, quindi:
[math] D = R [/math]
.
Determiniamo ora i punti di intersezione con gli assi:
[math] f(x) _|_ (x = 0) [/math]
[math] f(0) = 0^2 - 3 \cdot 0^{2/3} = 0 [/math]
Il punto individuato è
[math] (0 ; 0) [/math]
.
[math] f(x) _|_ (y = 0)[/math]
[math] f(x) = 0 \to x^2 - 3 x^{2/3} = 0 [/math]
[math] x^2 = 3 \root[3]{x^2} [/math]
[math] x^6 = 27 x^2 \to x^2 (x^4 - 27) = 0 [/math]
[math] x = +- \root[4]{27} , x = 0 [/math]
I punti individuati sono
[math] ( \root[4]{27} ; 0 ) [/math]
e
[math] ( - \root[4]{27} ; 0 ) [/math]
.
Quindi la funzione passa per l'origine e ha due punti di intersezione con l'asse x.
Notiamo che
[math] f(x) = f(-x)[/math]
, quindi la funzione è pari, ovvero simmetrica rispetto all'asse y.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, in questo caso, a
[math]+oo[/math]
e
[math]-oo[/math]
:
[math] lim_(x \to oo) x^2 - 3 x^{2/3} [/math]
Il limite può essere risolto immediatamente: le incognite presenti, infatti, sono di gradi diverso, e nella determinazione del limite si tiene conto di quella di grado più alto; abbiamo, quindi:
[math] lim_(x \to +oo) x^2 - 3 x^{2/3} = lim_(x \to -oo) x^2 - 3 x^{2/3} = + oo [/math]
La funzione, quindi, non presenta asintoti né orizzontali né verticali.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
[math] f'(x) = 2x - 3 \cdot 2/3 x^{-1/3} = 2x - frac(2)(x^{1/3}) = 2frac(x^{2/3} - 1)(x^{1/3}) [/math]
Troviamo i punti in cui la deriva prima si annulla:
[math] f'(x) = 0 \to 2frac(x^{2/3} - 1)(x^{1/3}) = 0 \to x^{2/3} = 1 \to x = \pm 1 [/math]
Studiamo il segno della derivata prima:
[math] f'(x) > 0 \to 2frac(x^{2/3} - 1)(x^{1/3}) > 0 [/math]
[math] N > 0 \to x^{2/3} - 1 > 0 \to x^2 > 1 \to -1
[math] D > 0 \to x^{1/3} > 0 \to x > 0 [/math]
Dallo studio del segno si ottiene:
[math] (-1 , 0) uu ( 1 , +oo) [/math]
; la funzione, quindi, è crescente in tale intervallo; poiché la funzione è pari, possiamo assumere che essa sia decrescente negli intervalli "speculari":
[math] (-oo , -1) uu ( 0 , 1) [/math]
.
Notiamo, quindi, che i punti in cui
[math] x = -1[/math]
e
[math] x = 1[/math]
sono punti di minimo per la funzione.
Poiché la funzione non presenta asintoti orizzontali, cerchiamo la eventuale presenza di asintoti obliqui:
[math] lim_(x \to 0) frac(f(x) )(x) = frac(x^2 - 2 x^{2/3})(x) = oo [/math]
Essendo tale limite infinito, la funzione non presenta asintoti obliqui.
Passiamo allo studio della derivata seconda:
[math] f''(x) = 2 \cdot frac(2/3 x^{-1/3} \cdot x^{1/3} - (x^{2/3} - 1) \cdot 1/3 x^{-2/3} )(x^{2/3}) = [/math]
[math] 2 \cdot frac(2/3 - 1/3 + 1/3 x^{-2/3} )(x^{2/3}) = [/math]
[math] 2/3 frac(1 + x^{-2/3} )(x^{2/3}) [/math]
Troviamo i punti in cui la deriva seconda si annulla:
[math] f''(x) = 0 \to 2/3 frac(1 + x^{-2/3} )(x^{2/3}) = 0 \to 1 + x^{-2/3} = 0 [/math]
La quantità al numeratore è sempre positiva, quindi la derivata seconda non si annulla mai; ciò significa che , essendo positiva la derivata seconda, la funzione presenta una concavità verso l'alto su tutto
[math]R[/math]
.
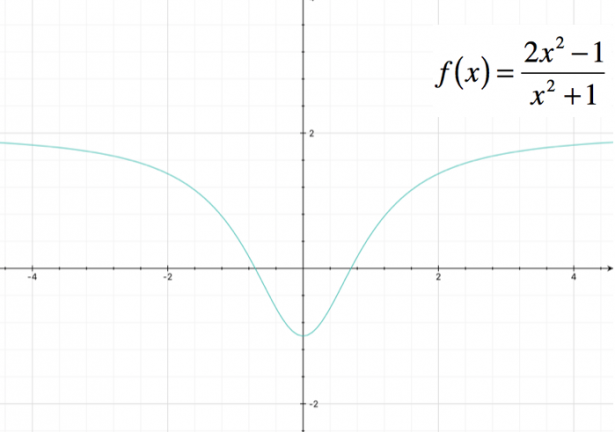
Possiamo quindi procedere rappresentando il grafico della funzione:
Potrebbe interessarti anche