_stan
di _stan
(320 punti)
7' di lettura
La funzione arcotangente è definita su tutto R, quindi le uniche condizioni che dobbiamo imporre riguardano l'argomento del logaritmo. Poniamo, quindi, tale argomento maggiore di zero:

[math]frac(x)( (x+3) \cdot |x+4| ) > 0[/math]

[math]x > 0[/math]

[math]x+3 > 0[/math]

[math]|x+4|>0[/math]

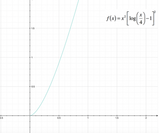
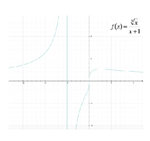
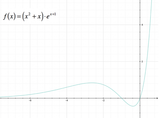
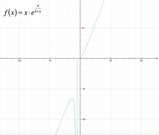
Dallo studio del segno si ottengono i seguenti intervalli:

[math] x 0 , x != -4[/math]

Quindi abbiamo:

[math] D = (-oo ; -4) uu (-4 ; -3) uu (0 ; +oo) [/math]
.

Per semplicità, nello svolgimento dei prossimi calcoli è conveniente eliminare il valore assoluto, e per farlo ricordiamo la proprietà dei valori assoluti per cui:

[math] |x| = x text( se ) x >= 0[/math]

[math] |x| = -x text( se ) x

In questo caso, quindi, possiamo assumere:

[math] f(x) = arc\\tan( \\log( frac(x)( (x+3) \cdot (x+4) ) ) ) text(se) x > -4 [/math]

[math] f(x) = arc\\tan( \\log( frac(x)( (x+3) \cdot (-x-4) ) ) ) text(se) x

Determiniamo ora i punti di intersezione con gli assi:

[math] f(x) _|_ (y = 0)[/math]

Se

[math]x > -4[/math]
:

[math]arc\\tan( \\log( frac(x)( (x+3) \cdot (x+4) ) ) ) = 0 \to \\log( frac(x)( (x+3) \cdot (x+4) ) ) = 0[/math]

[math] frac(x)( (x+3) \cdot (x+4) ) = 1 \to frac(x - x^2 - 3x - 4x - 12)( (x+3) \cdot (x+4) ) = 0[/math]

[math] x^2 + 6x + 12 = 0[/math]

L'equazione è priva di soluzioni reali (delta negativo), quindi la funzione non ha punti di intersezione con l'asse x per

[math] x > -4[/math]
.

Se

[math]x :

[math]arc\\tan( \\log( frac(x)( (x+3) \cdot (-x-4) ) ) ) = 0 \to \\log( frac(x)( (x+3) \cdot (-x-4) ) ) = 0[/math]

[math] frac(x)( (x+3) \cdot (-x-4) ) = 1 \to frac(x + x^2 + 3x + 4x + 12)( (x+3) \cdot (-x-4) ) = 0[/math]

[math] x^2 + 8x + 12 = 0 \to x = -6 vee x = -2[/math]

Possiamo accettare come soluzione solo

[math] x = -6[/math]
; di conseguenza, il punto di intersezione è
[math] ( -6 ; 0 ) [/math]
.

Verifichiamo se la funzione è pari o dispari:

[math] f(-x) = arc\\tan( \\log( frac(-x)( (-x+3) \cdot |-x+4| ) ) ) [/math]

La funzione quindi non è ne pari ne dispari.

Determiniamo gli intervalli in cui la funzione è positiva; per

[math]x > -4[/math]
si ha:

[math] arc\\tan( \\log( frac(x)( (x+3) \cdot (x+4) ) ) ) > 0 \to \\log( frac(x)( (x+3) \cdot (x+4) ) ) > 0[/math]

[math] frac(x)( (x+3) \cdot (x+4) ) > 1 \to frac(x-x^2 - 7x - 12)( (x+3) \cdot (x+4) ) > 0 \to [/math]

[math] frac( -x^2 - 6x - 12)( (x+3) \cdot (x+4) ) > 0 [/math]

Tale disequazione è verificata per valori di x nell'intervallo

[math](-4;-3)[/math]
; la funzione, quindi, è positiva in tale intervallo.

Vediamo ora il caso

[math]x si ha:

[math] arc\\tan( \\log( frac(x)( (x+3) \cdot (-x-4) ) ) ) > 0 \to \\log( frac(x)( (x+3) \cdot (-x-4) ) ) > 0[/math]

[math] frac(x)( (x+3) \cdot (-x-4) ) > 1 \to frac(x)( (x+3) \cdot (x+4) )

[math] frac(x+x^2 + 7x + 12)( (x+3) \cdot (x+4) )

Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo dal limite a

[math]+oo[/math]
:

[math] lim_(x \to +oo) arc\\tan( \\log( frac(x)( (x+3) \cdot |x+4| ) ) ) = lim_(x \to +oo) arc\\tan( \\log( frac(x)( (x+3) \cdot (x+4) ) ) ) = - π/2[/math]

Passiamo ora al limite a

[math]-oo[/math]
:

[math] lim_(x \to +oo) arc\\tan( \\log( frac(x)( (x+3) \cdot |x+4| ) ) ) = lim_(x \to +oo) arc\\tan( \\log( frac(x)( (x+3) \cdot (-x-4) ) ) ) = - π/2[/math]

Quindi, la retta di equazione

[math] y = - π/2[/math]
è asintoto orizzontale (destro e sinistro) per la funzione.

Studiamo ora il comportamento della funzione quando si avvicina ai punti che sono esclusi dal dominio; cominciamo con il caso

[math] x \to 3^-[/math]
:

[math] lim_(x \to -3^-) arc\\tan( \\log( frac(x)( (x+3) \cdot |x+4| ) ) ) = lim_(x \to -3^-) arc\\tan( \\log( frac(x)( (x+3) \cdot (x+4) ) ) ) = π/2[/math]

Allo stesso modo, per

[math]x \to 0^+[/math]
:

[math] lim_(x \to 0^+) arc\\tan( \\log( frac(x)( (x+3) \cdot |x+4| ) ) ) = lim_(x \to 0^+) arc\\tan( \\log( frac(x)( (x+3) \cdot (x+4) ) ) ) = -π/2[/math]

Infine, per

[math] x \to -4[/math]
si ha:

[math] lim_(x \to -4^+) arc\\tan( \\log( frac(x)( (x+3) \cdot |x+4| ) ) ) = lim_(x \to -4^+) arc\\tan( \\log( frac(x)( (x+3) \cdot (x+4) ) ) ) = π/2[/math]

[math] lim_(x \to -4^-) arc\\tan( \\log( frac(x)( (x+3) \cdot |x+4| ) ) ) = lim_(x \to -4^-) arc\\tan( \\log( frac(x)( (x+3) \cdot (-x-4) ) ) ) = π/2[/math]

La funzione, quindi, non presenta asintoti verticali.

Cerchiamo eventuali punti di massimo o minimo studiando la derivata prima:

[math] f'(x) = frac( frac(x^2 + 7x + 12 - 2x^2 - 7x)((x^2 + 7x + 12)^2) )( 1 + \\log^2(frac(x)(x^2 + 7x + 12)) ) \cdot frac(x^2 + 7x + 12)(x) = [/math]

[math] frac(1)( 1 + \\log^2(frac(x)(x^2 + 7x + 12)) ) \cdot frac(12 - x^2)( x^3 + 7x^2 + 12x) [/math]

Troviamo i punti in cui la deriva prima si annulla:

[math] f'(x) = 0 \to frac(1)( 1 + \\log^2(frac(x)(x^2 + 7x + 12)) ) \cdot frac(12 - x^2)( x^3 + 7x^2 + 12x) = 0 [/math]

[math] 12 - x^2 = 0 \to x^2 = 12 \to x = \pm \sqrt{12} [/math]

Studiamo il segno della derivata prima:

[math] f'(x) > 0 \to frac(1)( 1 + \\log^2(frac(x)(x^2 + 7x + 12)) ) \cdot frac(12 - x^2)( x^3 + 7x^2 + 12x) > 0 [/math]

[math] 1 + \\log^2(frac(x)(x^2 + 7x + 12)) > 0 [/math]

[math] 12 - x^2 > 0 [/math]

[math] x^3 + 7x^2 + 12x > 0 [/math]

Dallo studio del segno si ottengono i seguenti intervalli:

[math] ( - oo , - 4 ) U ( -\sqrt{12} ; -3) U ( 0 ; \sqrt{12} ) [/math]
; la funzione, quindi, è crescente in tali intervalli.

Notiamo, quindi, che il punto individuato da

[math] x = - \sqrt{12} [/math]
è un punto di minimo relativo per la funzione, mentre il punto individuato da
[math] x = \sqrt{12} [/math]
è un punto di massimo relativo per la funzione.

In questo caso, il calcolo della derivata seconda si rivela troppo complesso; possiamo comunque tracciare il grafico approssimativo della funzione.

Nell'intervallo

[math] (-oo ; -3) [/math]
si avrà un grafico di questo tipo:

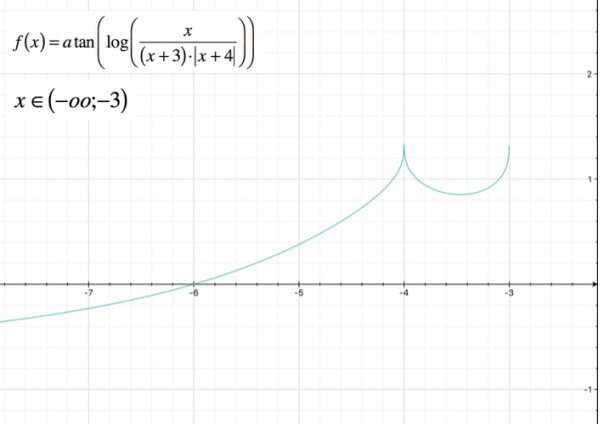
Mentre nell'intervallo

[math] (0 ; +oo) [/math]
si avrà:

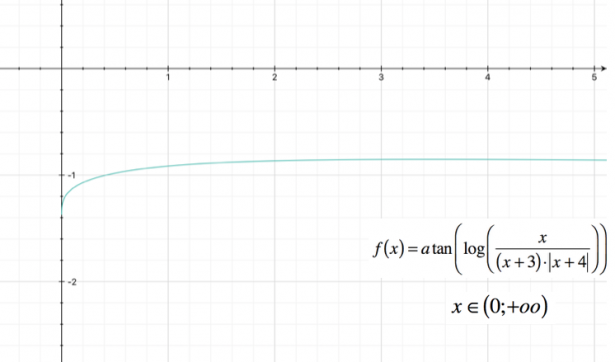
Potrebbe interessarti anche

Vuoi approfondire Algebra – Esercizi e Appunti di Algebra con un insegnante esperto?
Trovalo su Ripetizioni.it